Infinite Sequences and Series: Problems Plus
In this video I go over further into infinite sequences and series and this time go over the end-of-chapter Problems Plus section of advanced math questions. There are a total of 27 questions in this section: 1 example + 26 problems. These problems are more advanced than the typical questions in my calculus book and are a great way to test how well you know the concepts covered. Try to solve them yourself before watching the solution!
The topics covered in this video are listed below with their time stamps.
- Introduction - 0:00
- Problems Plus - 1:23
- Topics to Cover - 1:54
- Example - 2:29
- Mistake: I didn't write the first 3 terms correctly, see notes for correction: 16:32
- Problem 1 - 16:53
- Problem 2 - 23:58
- Problem 3 - 35:27
- Problem 4 - 1:05:21
- Problem 5 - 1:31:38
- Problem 6 - 2:03:57
- Problem 7 - 2:14:25
- Problem 8- 3:16:19
- Problem 9 - 3:44:25
- Problem 10 - 4:05:47
- Problem 11 - 4:21:35
- Problem 12 - 4:35:12
- Problem 13 - 4:56:02
- Problem 14 - 5:26:33
- Problem 15 - 5:38:41
- Problem 16 - 6:00:57
- Problem 17 - 6:16:06
- Problem 18 - 6:54:16
- Problem 19 - 7:23:42
- Problem 20 - 7:37:31
- Problem 21 - 8:04:29
- Problem 22 - 8:15:36
- Problem 23 - 8:39:05
- Problem 24 - 8:51:03
- Problem 25 - 9:43:11
- Problem 26 - 10:05:10
- PDF video notes: https://1drv.ms/b/s!As32ynv0LoaIiZg7o21H8ECtXaS0-Q
- Video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0FQ96Egr5R7fZGeDTIUKz8P
- Sequences and Series playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EXHAJ3vRg0T_kKEyPah1Lz
Watch Video On:
- 3Speak: https://3speak.tv/watch?v=mes/jhbzitnd
- Odysee: https://odysee.com/@mes:8/Sequences-and-Series-Problems-Plus:a
- BitChute: https://www.bitchute.com/video/AzLBSny9lGRC/
- Rumble: https://rumble.com/v1q7b7u-infinite-sequences-and-series-problems-plus.html
- DTube:
- YouTube: https://youtu.be/zjdkQIIdTbg
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
MES Links Telegram channel: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truthJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Calculus Book Reference
Note that I mainly follow along the following calculus book.
- Calculus: Early Transcendentals 7th Edition by James Stewart
- Note: The previous videos I used the 6th edition.
Infinite Sequences and Series: Problems Plus
At the end of each chapter in my calculus book, there are a series of advanced math problems called "Problems Plus".
They are a great way to fine-tune your mathematical skills!
If you can solve them, you can pretty much solve all of life…
Topics to Cover
I have created a list of the problems, which I will use to add the video timestamps.
- Example
- Problem 1
- Problem 2
- Problem 3
- Problem 4
- Problem 5
- Problem 6
- Problem 7
- Problem 8
- Problem 9
- Problem 10
- Problem 11
- Problem 12
- Problem 13
- Problem 14
- Problem 15
- Problem 16
- Problem 17
- Problem 18
- Problem 19
- Problem 20
- Problem 21
- Problem 22
- Problem 23
- Problem 24
- Problem 25
- Problem 26
Example
Find the sum of the series:
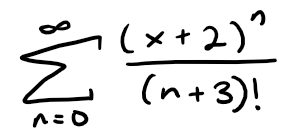
Solution:
The problem-solving principle that is relevant here is recognizing something familiar.
Does the given series look anything like a series that we already know?
Let's first do a recap on the Taylor series.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
Retrieved: 21 May 2022
Archive: https://archive.ph/wip/QVFhu
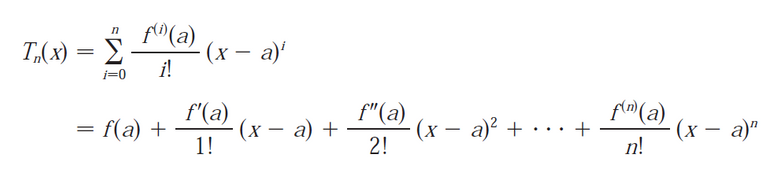
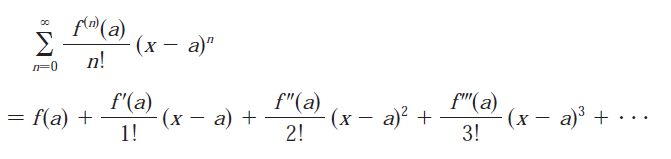

Note that a Maclaurin series is a special case of a Taylor series where a = 0.
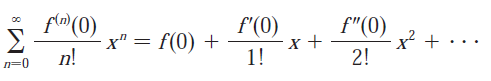
Below is a table of some functions that are equal to their corresponding Maclaurin series.

Recall also that R in the above table is the radius of convergence.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series
Retrieved: 21 May 2022
Archive: https://archive.ph/CGE8k

Well, it does have some ingredients in common with the Maclaurin series for the exponential function.
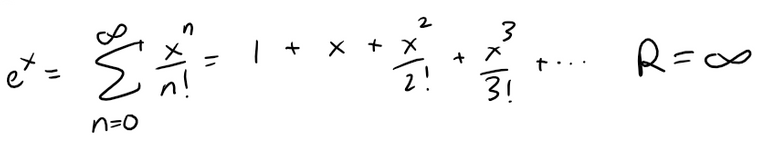
We can make this series look more like our given series by replacing x by x + 2:
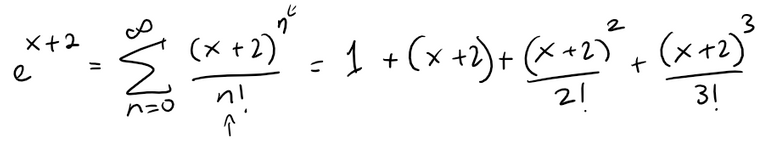
But here the exponent in the numerator matches the number in the denominator whose factorial is taken.
To make that happen in the given series in the example, let's multiply and divide by (x + 2)3:
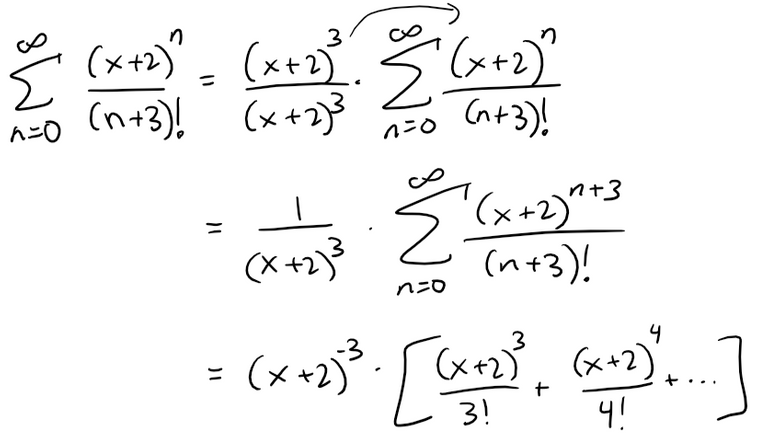
We see that the series between brackets is just the series for ex+2 with the first three terms missing.
So, we have:
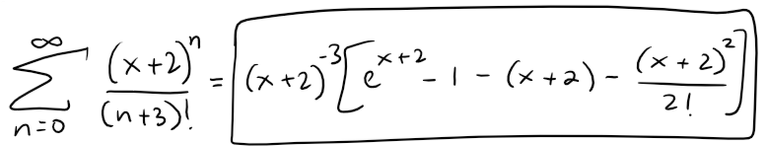
Problem 1
If f(x) = sin(x3), find f(15)(0).
Solution:
It would be far too much work to compute 15 derivatives of f.
The key idea is to remember that f(n)(0) occurs in the coefficient of xn in the Maclaurin series of f.
We start with the Maclaurin series for sin (from the earlier table above):
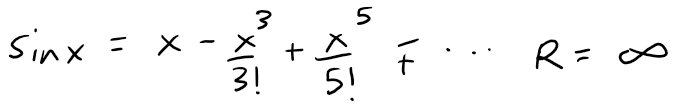
Then plugging in x3 we get:
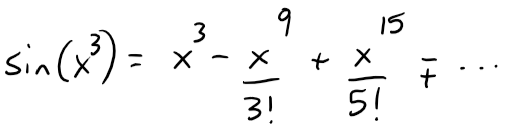
Recall the definition of the Maclaurin series:
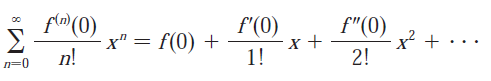
Thus at the x15 we can determine the corresponding derivative:
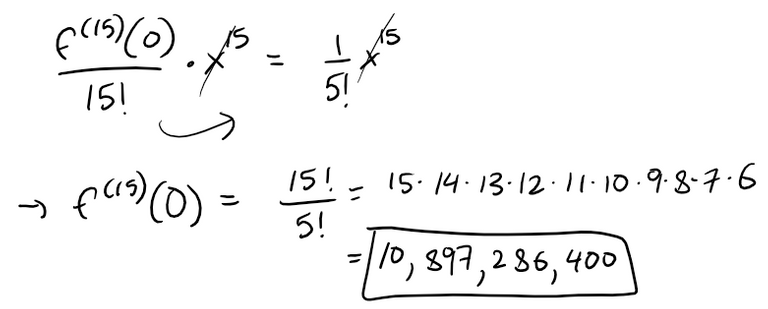
Calculation Check:
15∙14∙13∙12∙11∙10∙9∙8∙7∙6 = 1E10
15!/5! = 1E10Since my OneNote calculator is not that precise, we can use the Google Search alternative, Presearch.com, which pays out in $PRE cryptocurrency.
https://presearch.com/search?q=15!/5!
Retrieved: 18 August 2022
Archive: https://archive.ph/Hgo5X
Create an account using my referral link: https://presearch.com/signup?rid=2083256
Problem 2
A function f is defined by
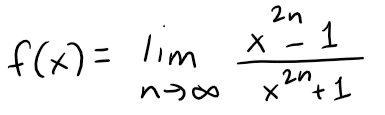
Where is f continuous?
Solution:
We use the problem-solving strategy of taking cases:
Case (i): |x| < 1
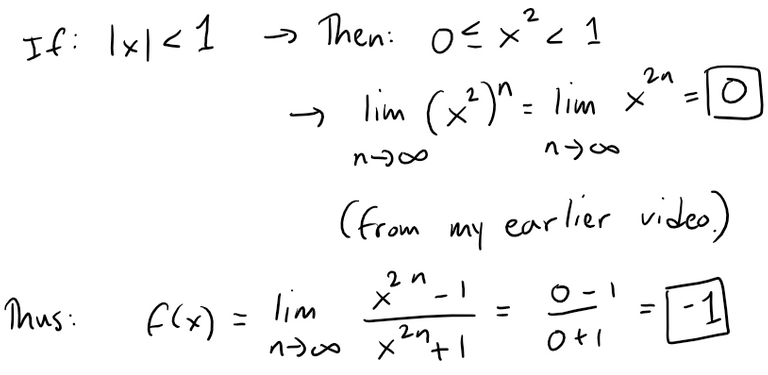
Recall from of my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-limits-squeeze-theorem-fibonacci-sequence-and-golden-ratio-more
Retrieved: 18 August 2022
Archive: https://archive.ph/wip/HjAui
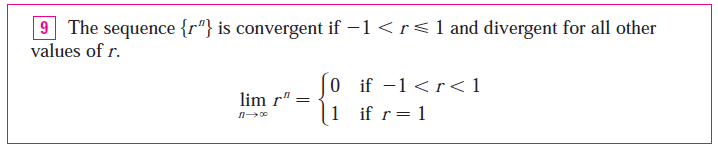
Case (ii): |x| = 1
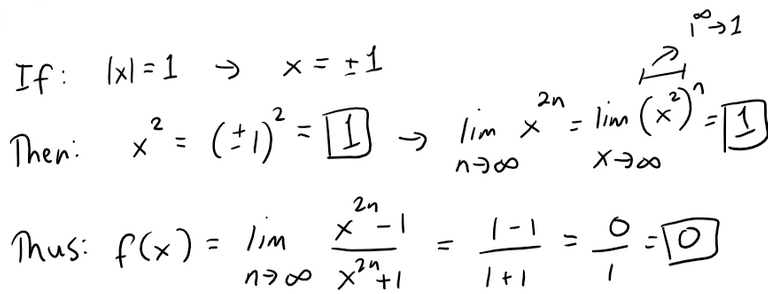
Case (iii): If |x| > 1
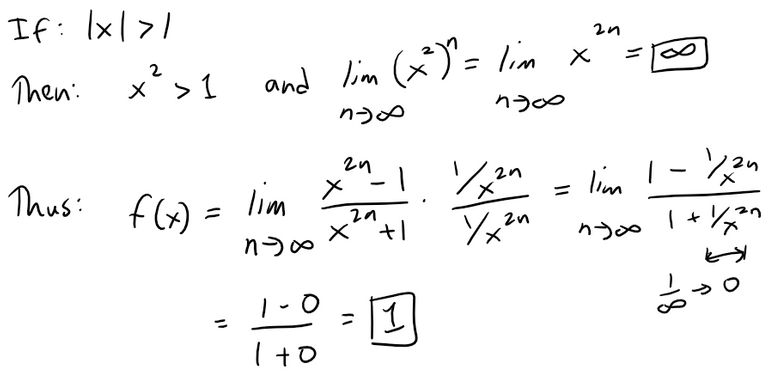
Putting it all together we have:
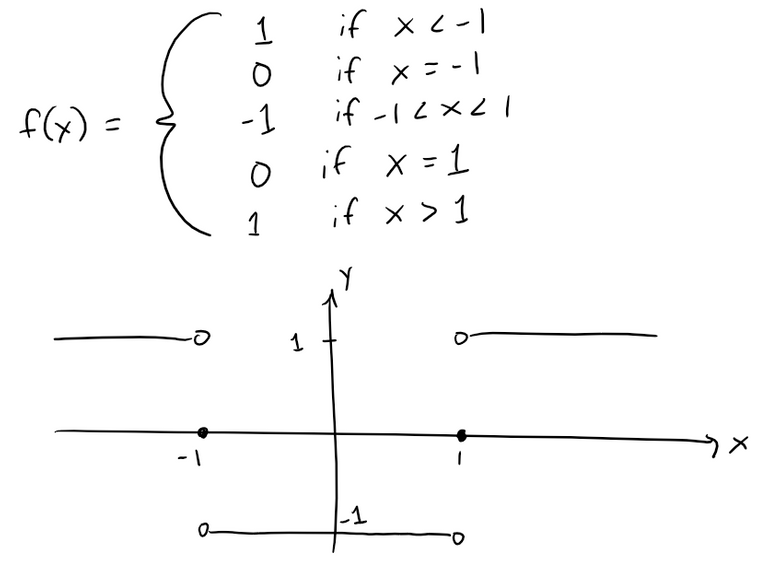
The graph shows that f is continuous everywhere except at x = ± 1.
Problem 3
(a) Show that:
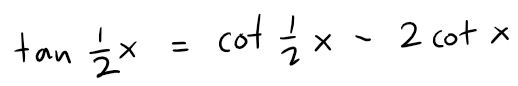
(b) Find the sum of the series:
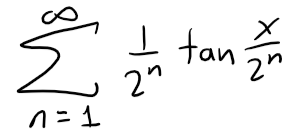
Solution to (a):
Recall the trigonometric identity from my earlier video:
https://peakd.com/mathematics/@mes/video-notes-trigonometric-identity-tan-x-y-proof
Retrieved: 18 August 2022
Archive: https://archive.ph/wip/glWnh

Using x = y = θ in the tan(x + y) identity, we get:

Solution to (b):
We need to find the sum of the following series:
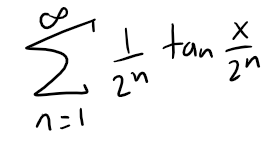
Using part (a) but replacing x with x / 2n - 1 we have:
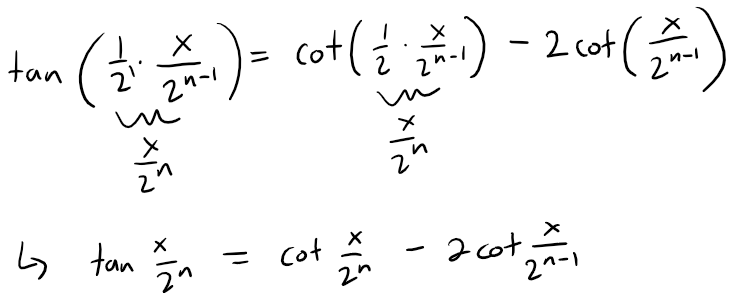
The n-th partial sum of the series is:
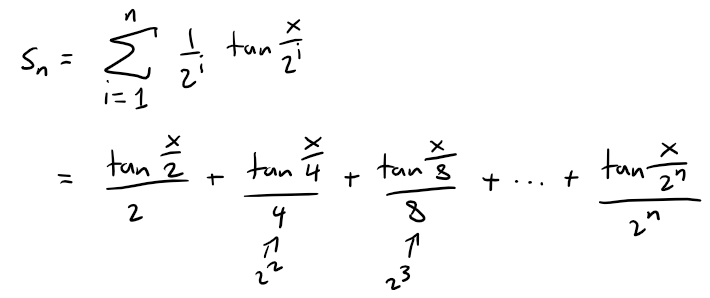
Now we can apply the identity to each tan function.

The above cancellations is known as the telescoping sum.
We have to take the limit of the partial sum to infinity.
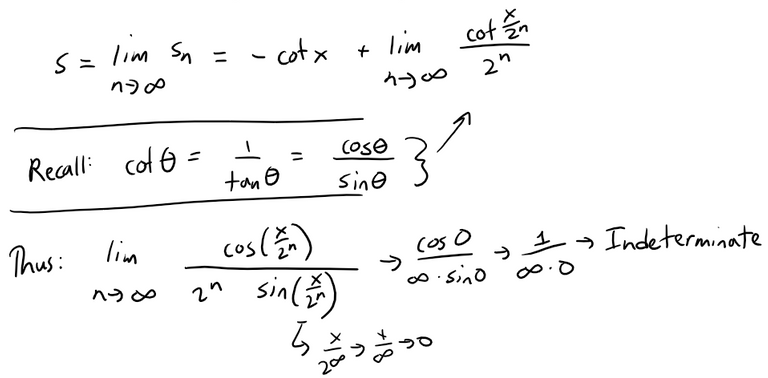
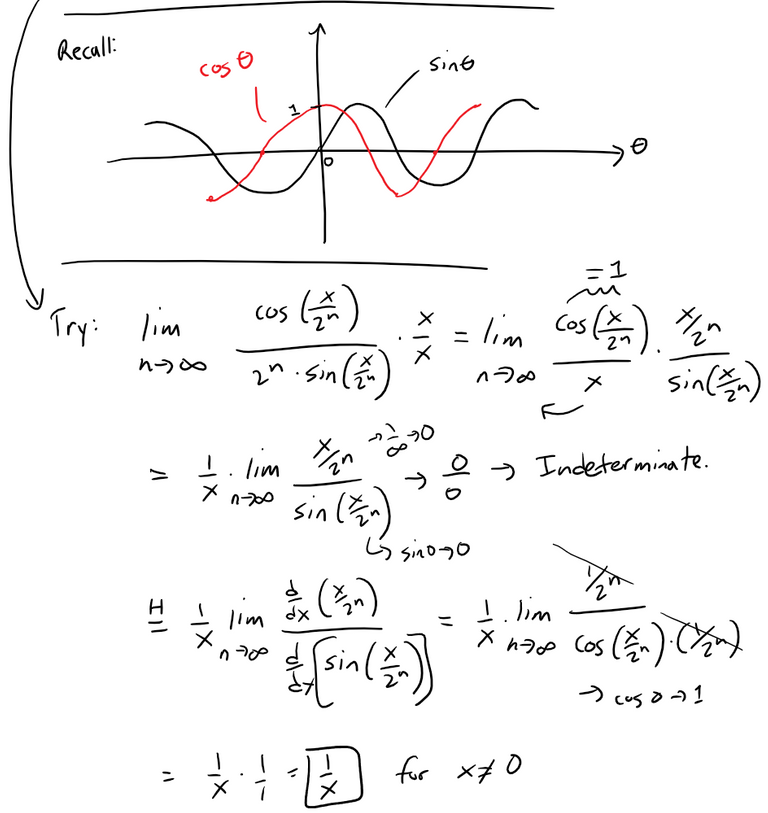
Note that I used the L'Hospital's Rule in the above limit.
Retrieved: 3 October 2020
Video notes archive: https://archive.vn/qiZ5r

Putting this all together we have, for x ≠ 0 and x ≠ kπ where k is any integer:
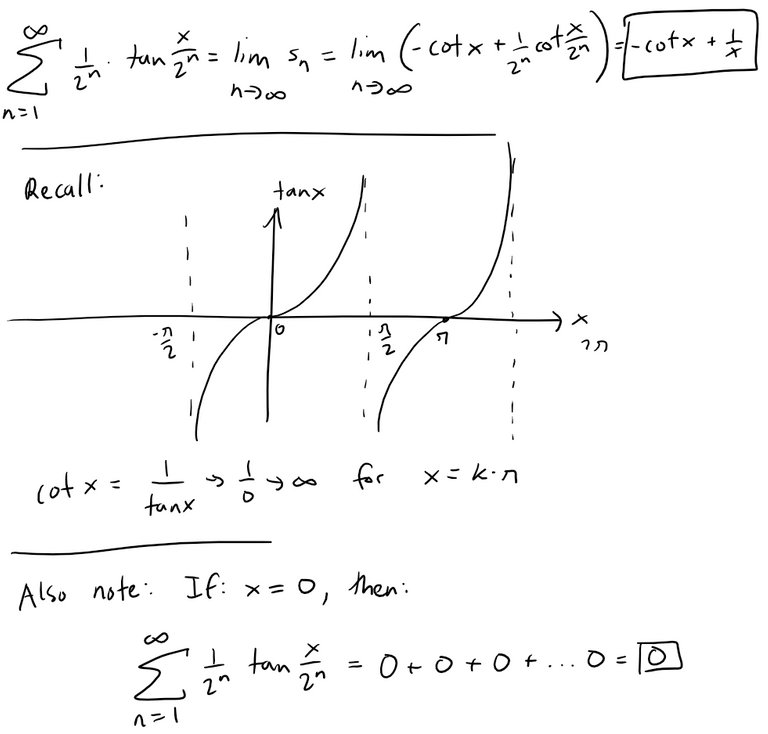
Problem 4
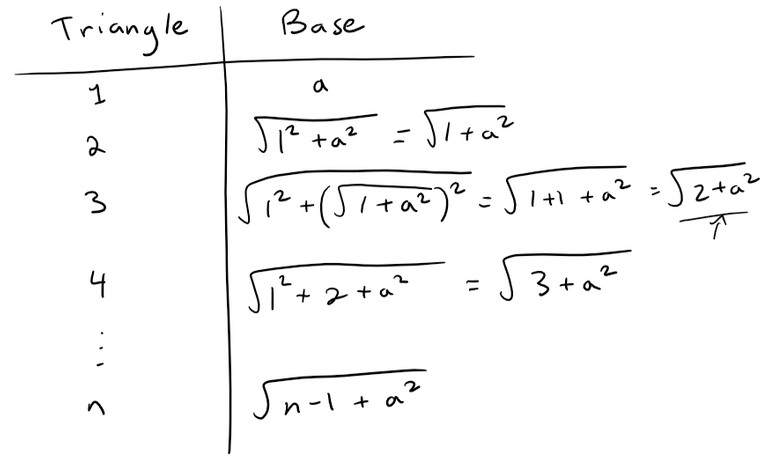
Let {Pn} be a sequence of points determined as in the figure.
Thus |AP1| = 1, |PnPn+1|= 2n-1, and angle APnPn+1 is a right angle.
Find limn→∞ ∠PnAPn+1.
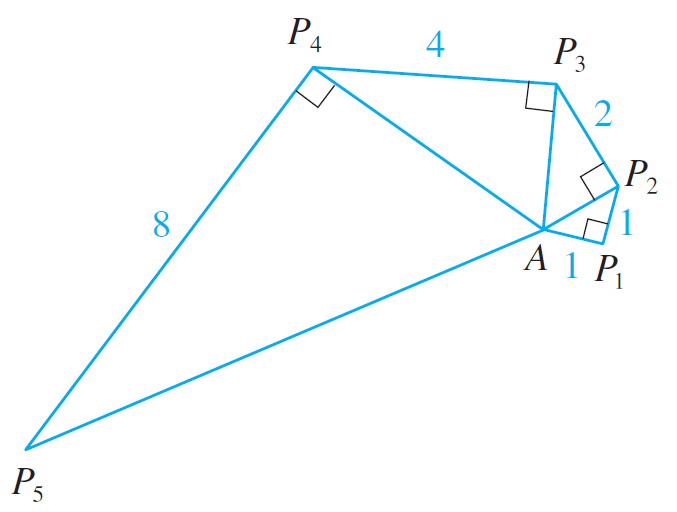
Solution:
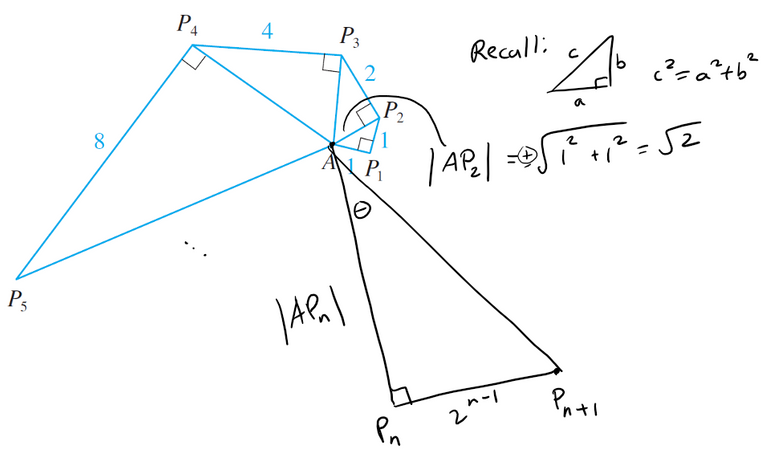
Note that the hypotenuse of the previous triangle becomes the base of the next one.
Using the Pythagorean Theorem we can write a formula for the square of the length |APn|.

For n ≥ 3, |APn|2 forms a geometric sum. Recall from my earlier video:
https://peakd.com/@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more
Retrieved: 20 August 2022
Archive: https://archive.ph/wip/nMDyh
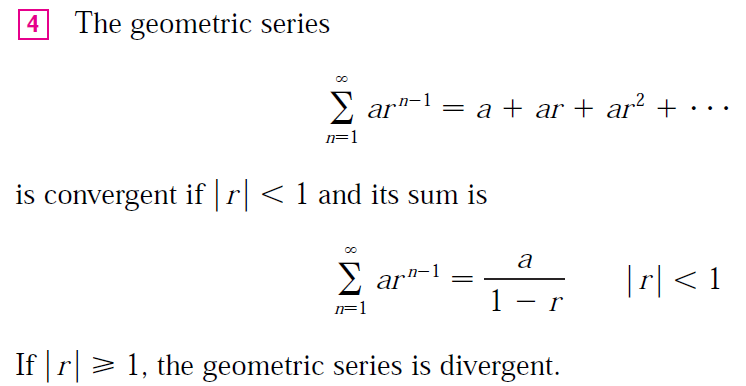
Note that the above formula is for an (infinite) geometric series. For a finite sum, recall the formula below:
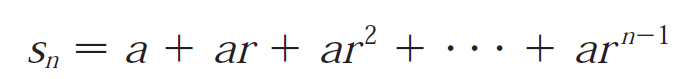
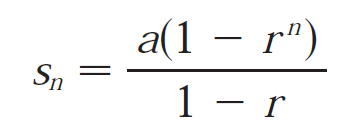
Since we are not yet finding the limit to infinity, let's apply the finite geometric sum (not infinite series).
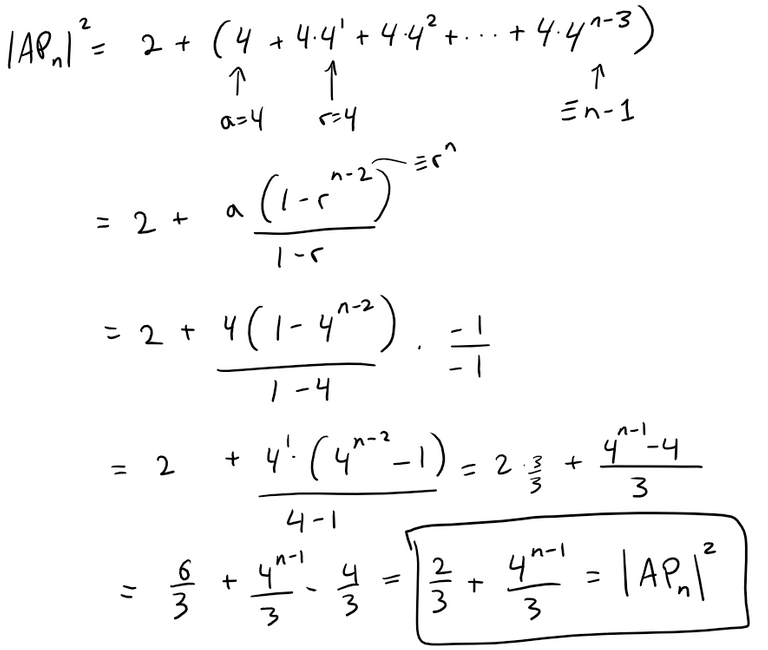
Now that we have the lengths of two sides of a right angle triangle, we can calculate the corresponding angle at A.
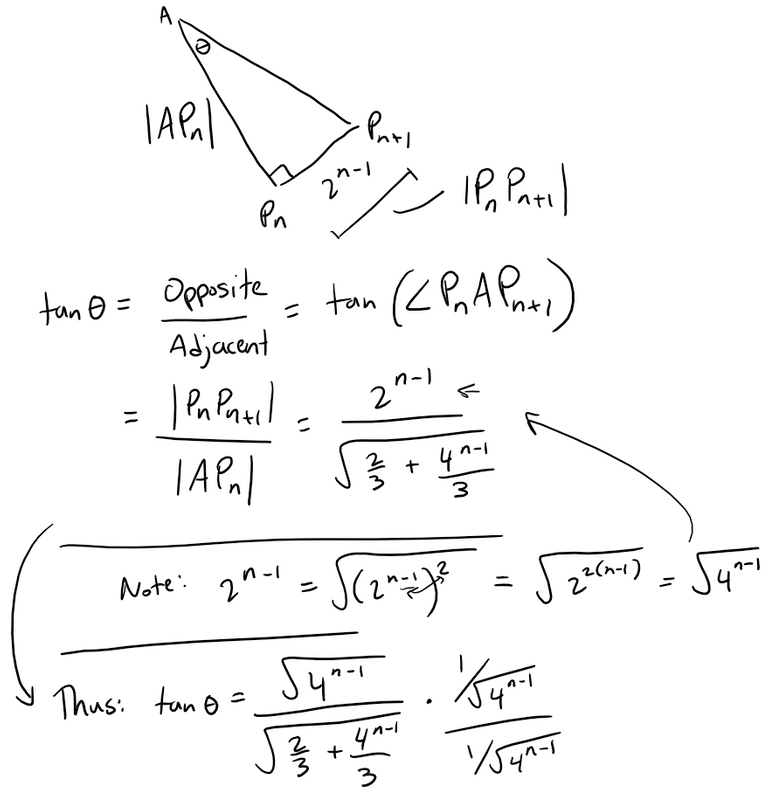
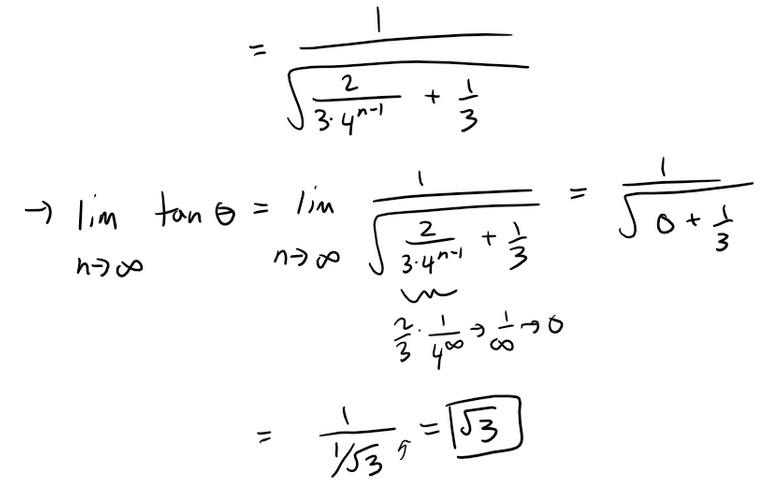
Recall the exact trigonometric ratios:

Problem 5
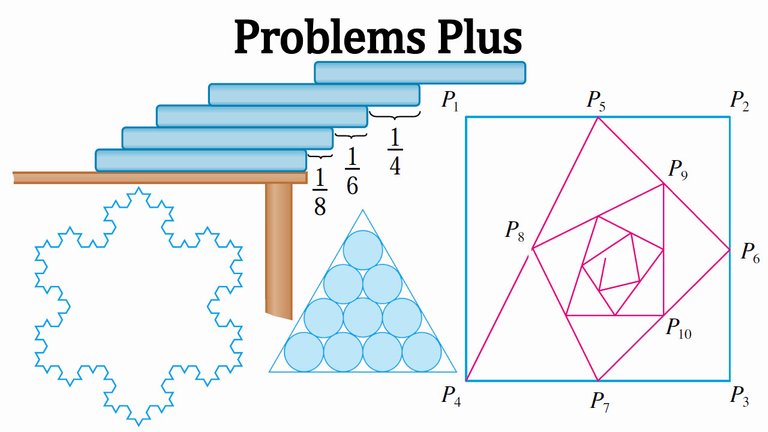
To construct the snowflake curve, start with an equilateral triangle with sides of length 1.
Step 1 in the construction is to divide each side into three equal parts, construct an equilateral triangle on the middle part, then delete the middle part.
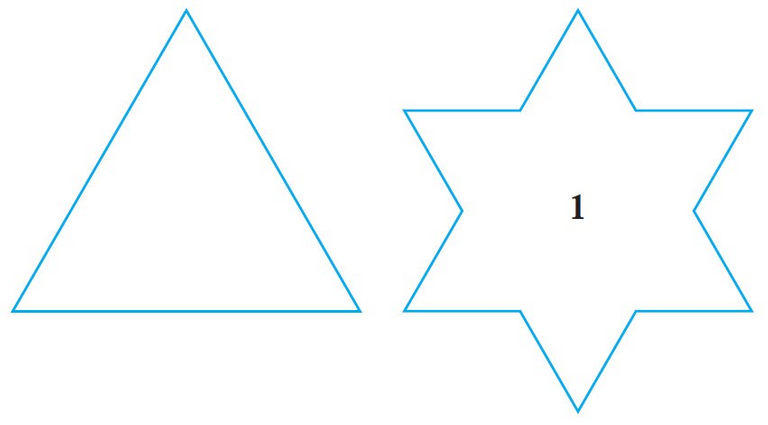
Step 2 is to repeat step 1 for each side of the resulting polygon. This process is repeated at each succeeding step.
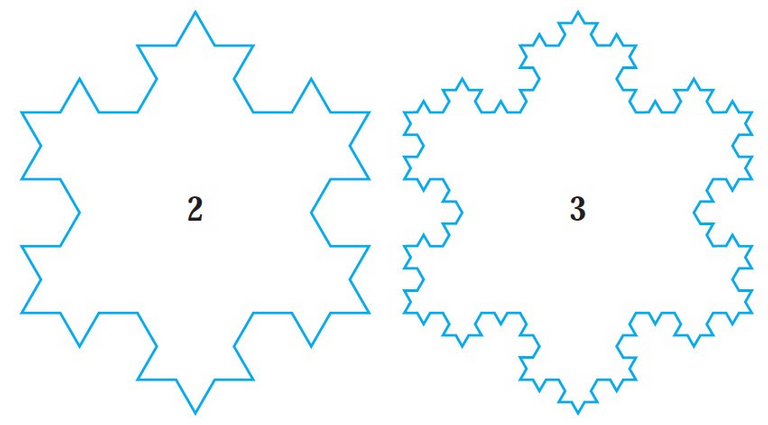
The snowflake curve is the curve that results from repeating this process indefinitely.
(a) Let sn, Ln, and pn represent the number of sides, the length of a side, and the total length of the n-th approximating curve (the curve obtained after step n of the construction), respectively.
Find formulas for sn, Ln, and pn.
(b) Show that pn → ∞ as n → ∞.
(c) Sum an infinite series to find the area enclosed by the snowflake curve.
Note: Parts (b) and (c) show that the snowflake curve is infinitely long but encloses only a finite area.
Solution to (a):
At each stage, each side is replaced by four shorter sides, each of length 1/3 of the side length of the preceding stage.
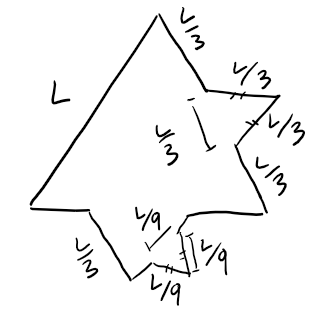
Writing s0 and L0 for the number of sides and length of the side of the initial triangle, we can generate the table below.
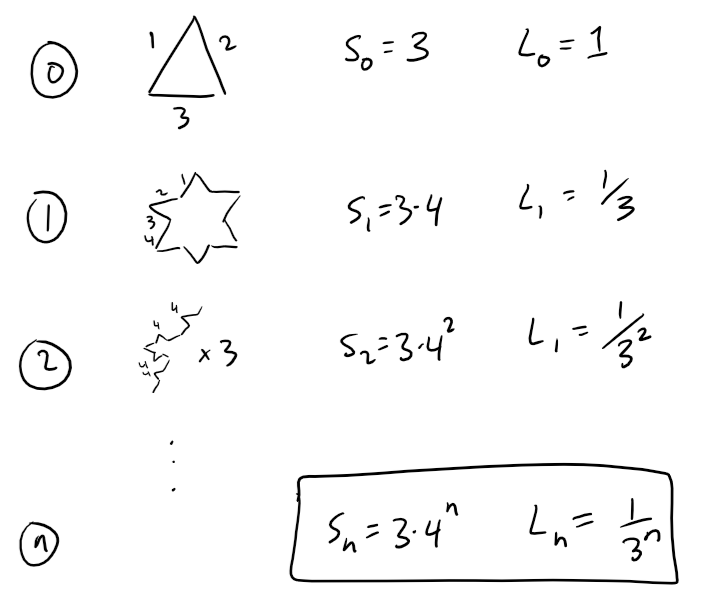
Multiplying the side length with the number of sides, we get the total length of the perimeter at the n-th stage of construction:
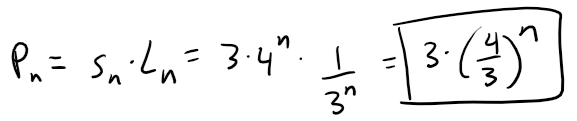
Solution to (b):
Taking the limit of the perimeter length we get:
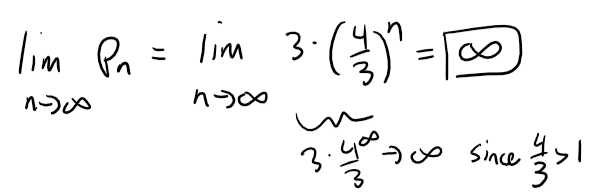
Solution to (c):
The area of each of the small triangles added at a given stage is one-ninth of the area of the triangle added at the preceding stage.
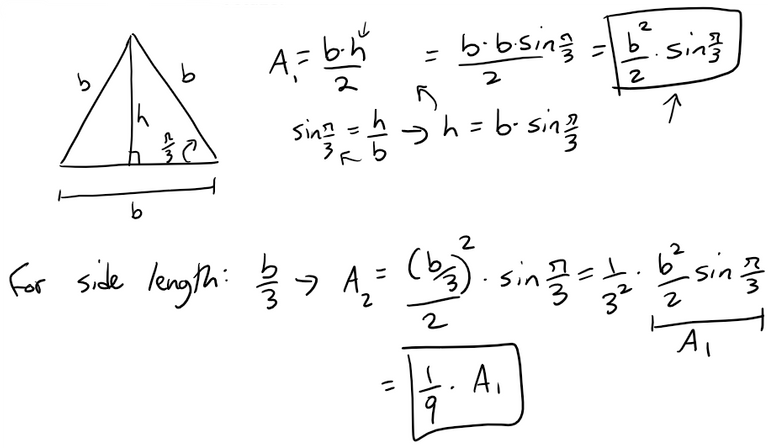
Let a be the area of the original triangle.
Then the area an of each of the small triangles added at stage n is:
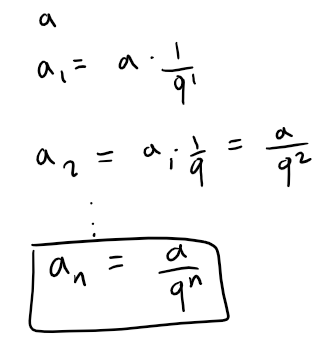
Since a small triangle is added to each side at every stage, it follows that the total area An added to the figure at the n-th stage is:
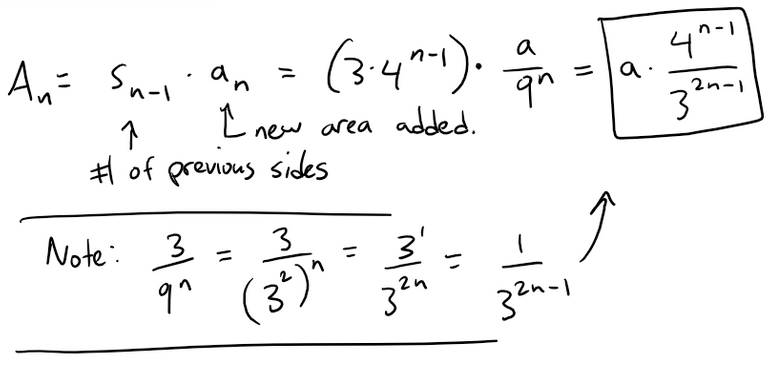
Then the total area enclosed by the snowflake curve is:

Using the formula for the sum of a convergent geometric series, we get:
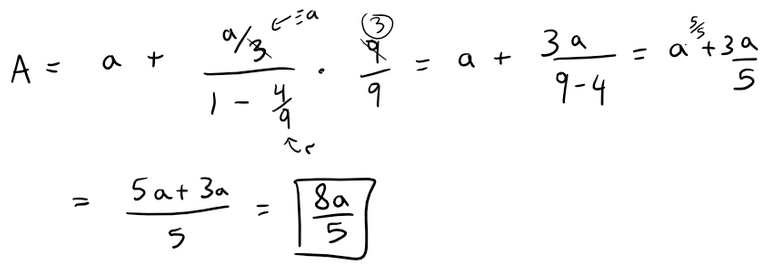
Now we just need to solve for the area of the original triangle.
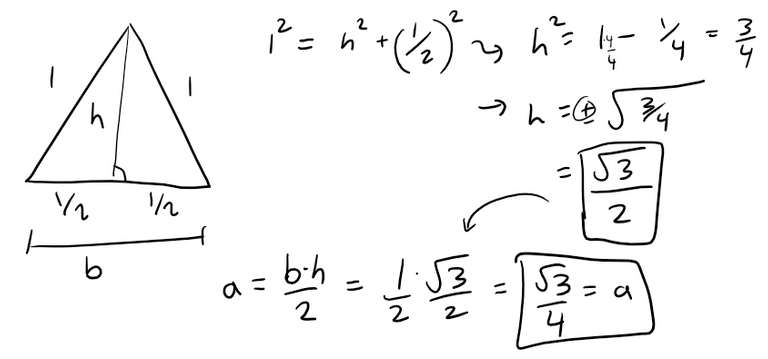
So the area enclosed by the snowflake curve is:
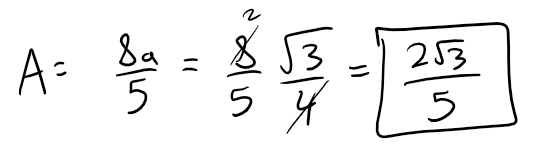
For further context, let's calculate the original vs snowflake areas.
a = sqrt(3)/4 = 0.433012701892219
A = sqrt(3)*2/5 = 0.692820323027551% increase: (0.692820323027551-0.433012701892219)/0.433012701892219 * 100 = 60.00000000000012 %
% increase: (sqrt(3)2/5-sqrt(3)/4)/(sqrt(3)/4)100 = 60.00000000000001 %
MES Note: Likely a calculation rounding error, since the exact answer is 60%.
Problem 6
Find the sum of the series:
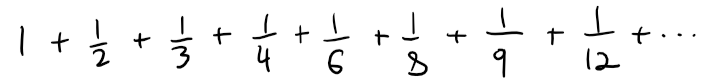
where the terms are the reciprocals of the positive integers whose only prime factors are 2s and 3s.
Solution:
Note that prime factors are prime numbers that can divide into a number cleanly. A prime number is a number that only has 2 factors, itself and 1.
Example: 1092
1092 / 2 = 546 / 2 = 273 / 3 = 91 / 7 = 13
Prime factors of 1092 are: 2, 2, 3, 7, 13.
The reciprocal of a number is of the form 1/x.
Example: 1092
The reciprocal of 1092 is 1/1092.
Let's call the series S.
Then every term in S is of the form:
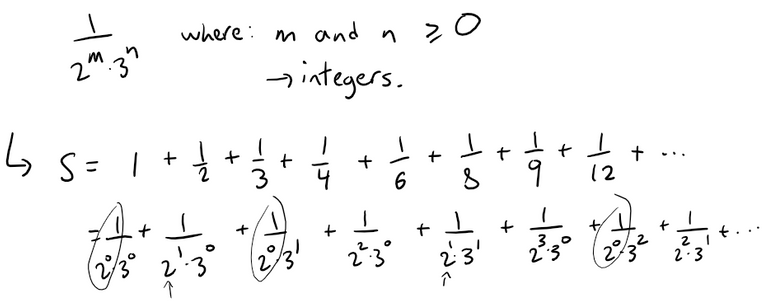
Furthermore, each term occurs only once.
We can now apply a double summation and noticing that we obtain 2 convergent geometric series.
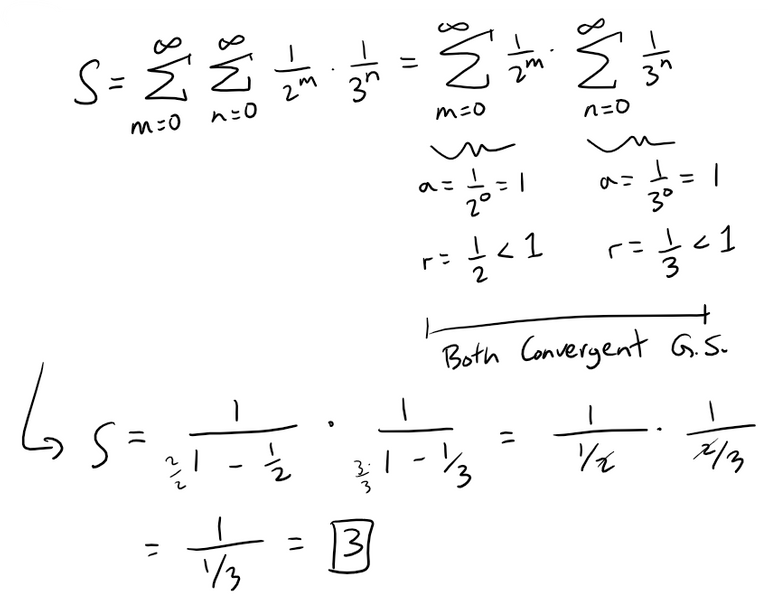
Problem 7
(a) Show that for xy ≠ 1,
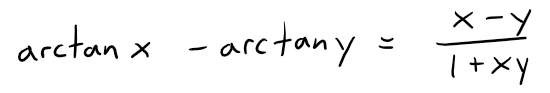
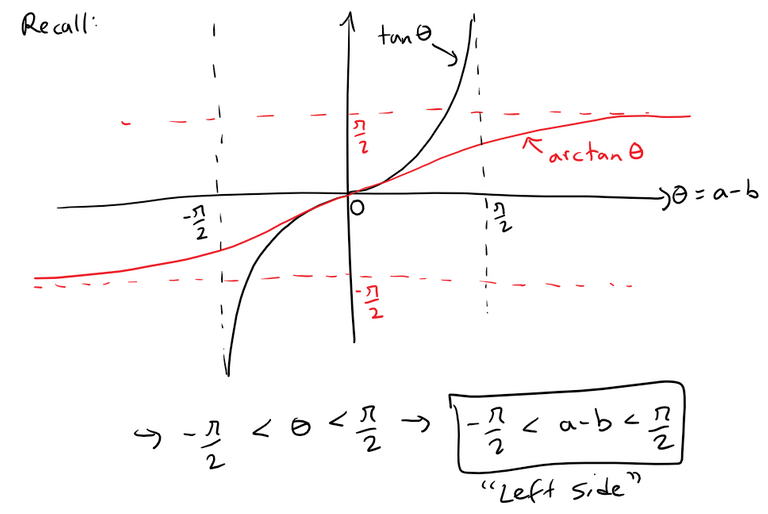
if the left side lies between -π/2 and π/2.
(b) Show that:
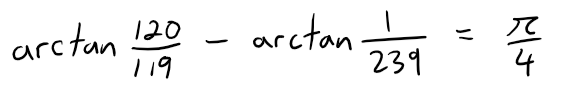
(c) Deduce the following formula of John Machin (1680 - 1751):
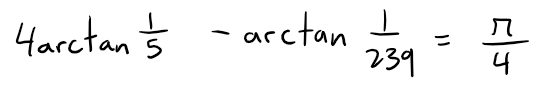
(d) Use the Maclaurin series for arctan to show that:
0.1973955597 < arctan 1/5 < 0.1973955616
(e) Show that:
0.004184075 < arctan 1/239 < 0.004184077
(f) Deduce that, correct to seven decimal places, π ≈ 3.1415927.
Machin used this method in 1706 to find π correct to 100 decimal places.
Recently, with the aid of computers, the value of π has been computed to increasingly greater accuracy.
In 2009 T. Daisuke and his team computed the value of π to more than two trillion decimal places!
Solution to (a):
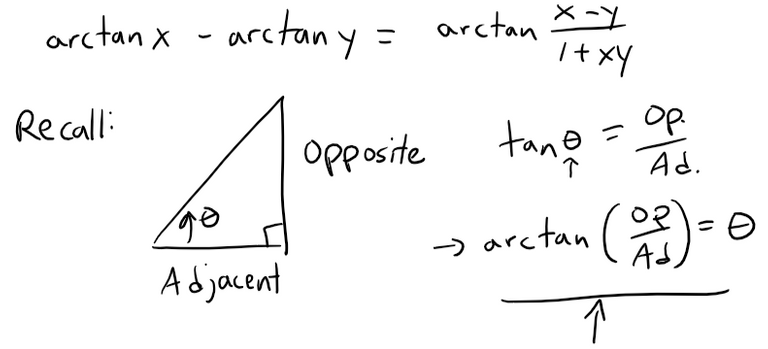
Let a = arctan x and b = arctan y.

Recall the earlier formula I referenced.
https://peakd.com/mathematics/@mes/video-notes-trigonometric-identity-tan-x-y-proof

Using the second formula we have:
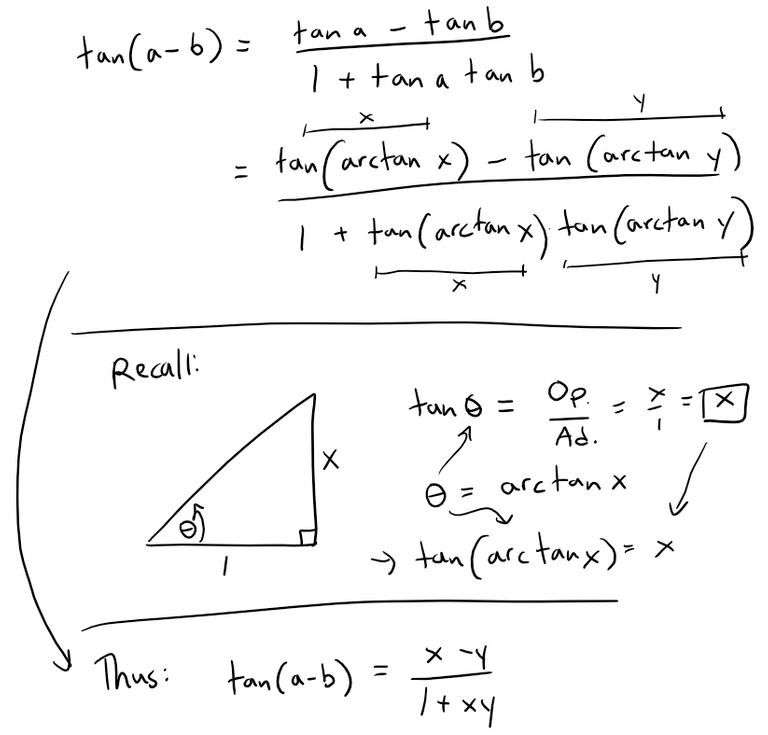
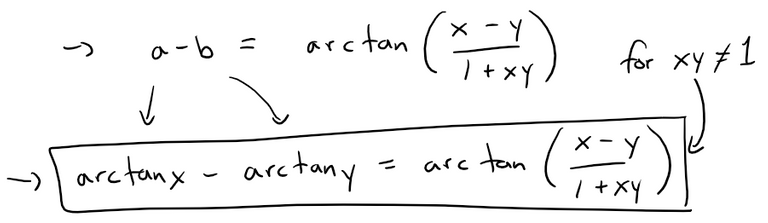
Note that the left side is between -π/2 and π/2.
Note that if xy = 1, then:
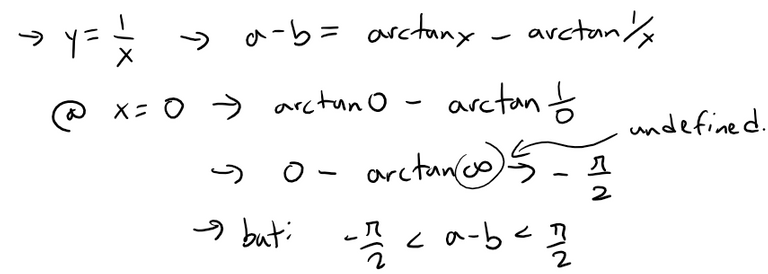
Solution to (b):
From (a) we have:
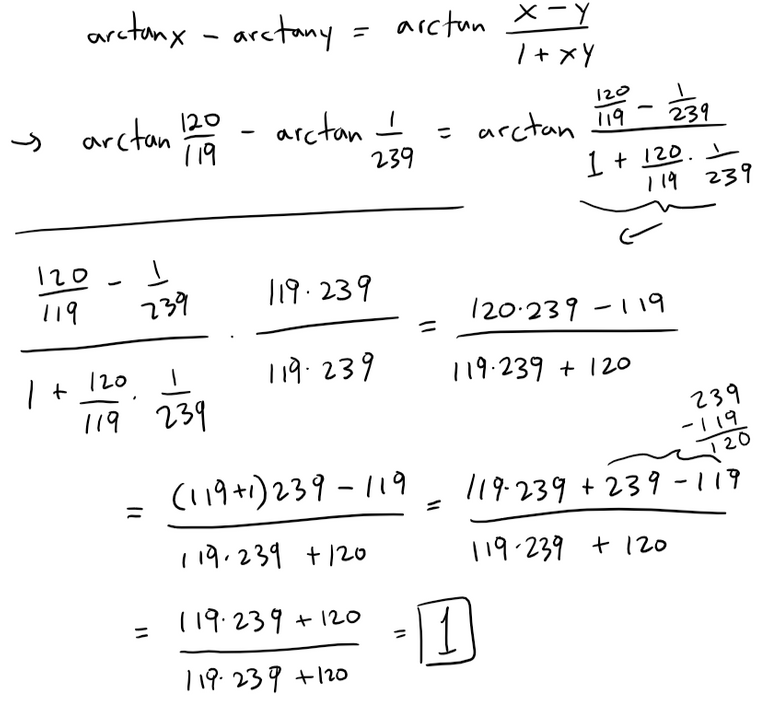
MES Calculation Check:
120∙239 - 119 = 28,561
119∙239 + 120 = 28,561(120/119 - 1/239) / (1 + 120/119 ∙ 1/239) = 1
Now we can recall our exact trigonometric ratios.
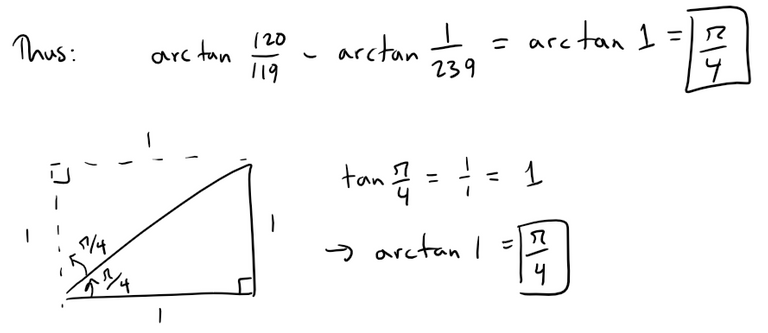
Solution to (c):
We are asked to show:
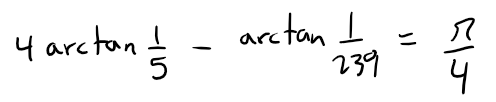
Replacing y by -y in the formula of part (a), we get:
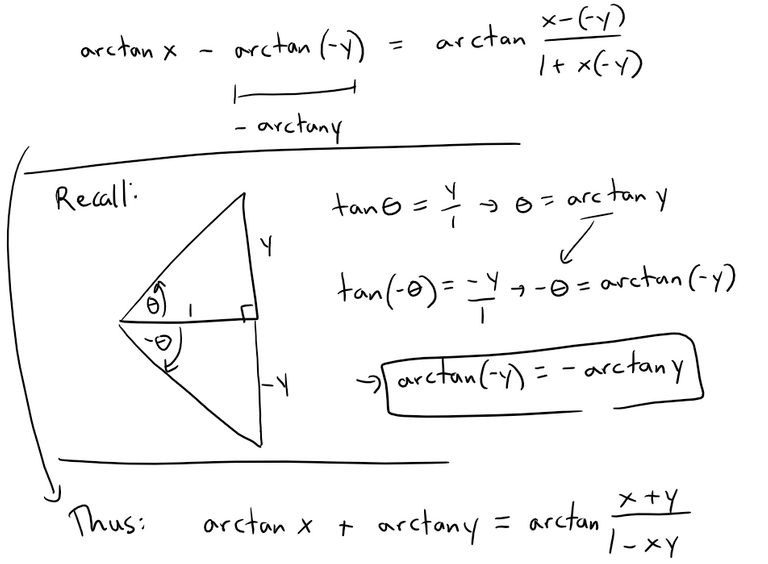
We did this so that we can use addition in the formula we are asked to show.


Thus, from part (b), we have:

Solution to (d):
We are asked to use the Maclaurin series for arctan to show that:
0.1973955597 < arctan 1/5 < 0.1973955616
Recall from the earlier table above.
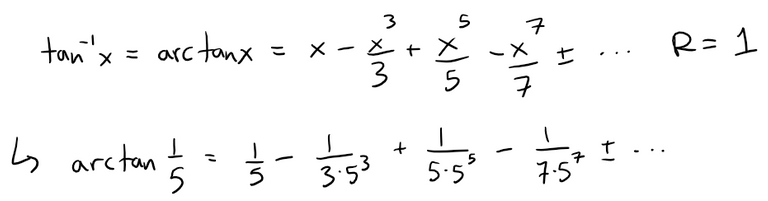
This is an alternating series and the size of the terms decreases to 0, so we can apply the Alternating Series Estimation Theorem, as recapped from my earlier video below.
https://peakd.com/@mes/infinite-sequences-and-series-alternating-tests
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/nhaeA

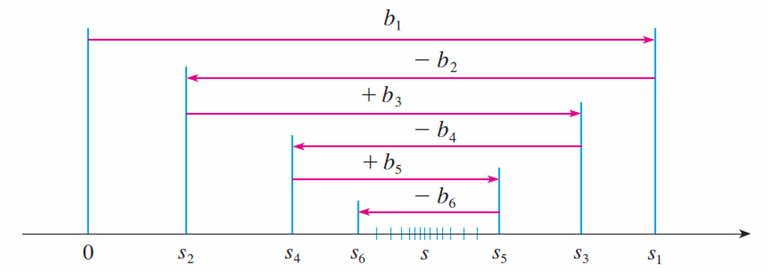


Thus, by the Alternating Series Estimation Theorem, the sum will be between each successive partial sum; and the error is the absolute value of the next term.
Show that: 0.1973955597 < arctan 1/5 < 0.1973955616
s1 = 1/5 = 0.2
s2 = 1/5 - 1/(3∙5^3) = 0.1973
s3 = 1/5 - 1/(3∙5^3) + 1/(5∙5^5) = 0.1974
s4 = 1/5 - 1/(3∙5^3) + 1/(5∙5^5) - 1/(7∙5^7) = >0.1974 … need to use a more powerful calculator.
…
s5 using Wolfram Alpha: https://www.wolframalpha.com/input...
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/7zH7Z
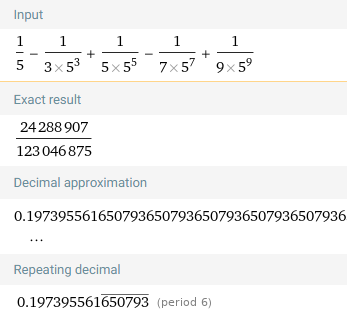
s6 using Wolfram Alpha: https://www.wolframalpha.com/input...
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/85ltL
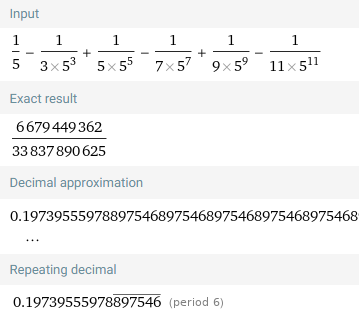
Thus the sum lies between s5 and s6:
s6 < arctan 1/5 < s7
0.1973955597… < arctan 1/5 < 0.1973955616…
This is the same as that we were asked to show:
0.1973955597 < arctan 1/5 < 0.1973955616
Note that the Solution manual rounds up to:
0.197395560 < arctan 1/5 < 0.197395562
Solution to (e):
We are now asked to show that:
0.004184075 < arctan 1/239 < 0.004184077
Using the series in part (d) we get:
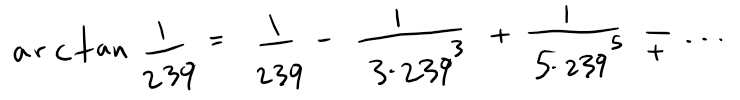
Since we are asked to determine the sum to 9 decimal places, we can calculate the corresponding remainder.
R2 = |s - s2| ≤ b2 = 1/(5∙239^5) = 0.0 (need to use a more powerful calculator).
https://www.wolframalpha.com/input?i=1%2F%285*239%5E5%29
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/kNOJy
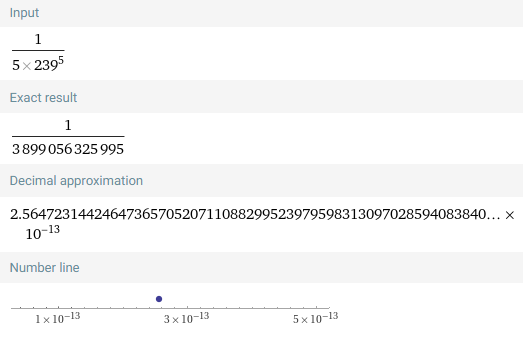
The third term is less than 2.6 x 10-13, thus by the Alternating Series Estimation Theorem we can just use s2:
https://www.wolframalpha.com/input?i=1%2F239-1%2F%283*239%5E3%29
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/YJGeg
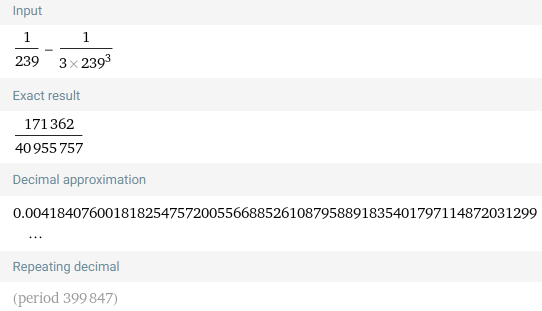
Thus s2 corresponds to the inequality we are asked to show:
s = arctan 1/239 ≈ s2 ≈ 0.004184076
0.004184075 < arctan 1/239 < 0.004184077
Note that we couldn't just use the inequality s2 < s < s1 because s1 is too large for the inequality we were asked to show.
s1 = 1/239 = 0.0041841004… > 0.004184077
Solution to (f):
We are asked to show that
π ≈ 3.1415927
From part (c) we can deduce that:
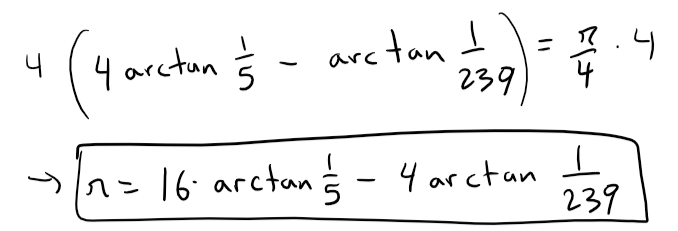
Recall from parts (d) and (e):
0.1973955597 < arctan 1/5 < 0.1973955616
0.004184075 < arctan 1/239 < 0.004184077
Thus we can apply add each inequality into our formula for π.
16∙(0.1973955597) - 4∙(0.004184077) < π < 16∙(0.1973955616) - 4∙(0.004184075)
Calculating this out we get:
16∙(0.1973955597) - 4∙(0.004184077) = 3.1415926472
16∙(0.1973955616) - 4∙(0.004184075) = 3.1415926856
3.1415926472 < π < 3.1415926856
Rounding to 7 decimal places we get:
3.1415926 < π < 3.1415927
Using the upper bound we get the estimation:
π ≈ 3.1415927
MES Calculation Check:
Pi = 3.141592653589793
Problem 8
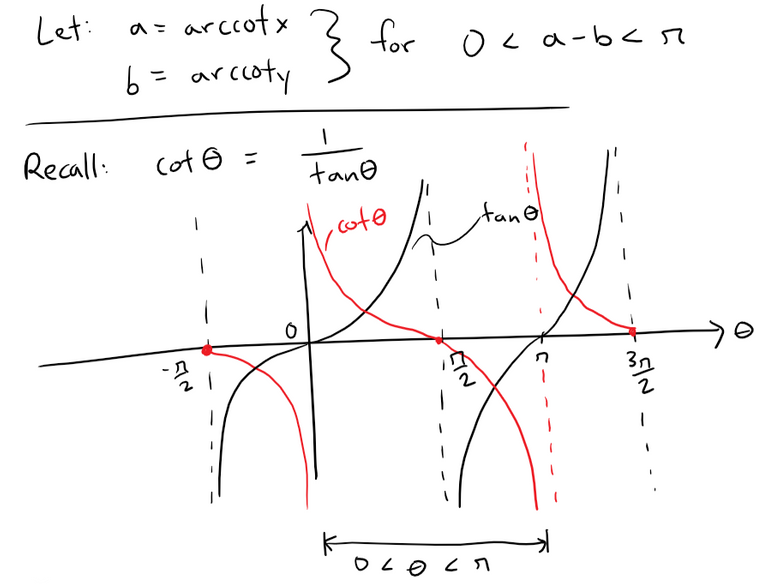
(a) Prove a formula similar to the one in Problem 7(a) but involving arccot instead of arctan.
(b) Find the sum of the series:
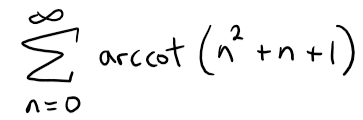
Solution to (a):
Recall from Problem 7(a) that we started off with the tan(x - y) trigonometric identity:
https://peakd.com/mathematics/@mes/video-notes-trigonometric-identity-tan-x-y-proof

Let's use the same identity but convert it to the form with arccot.
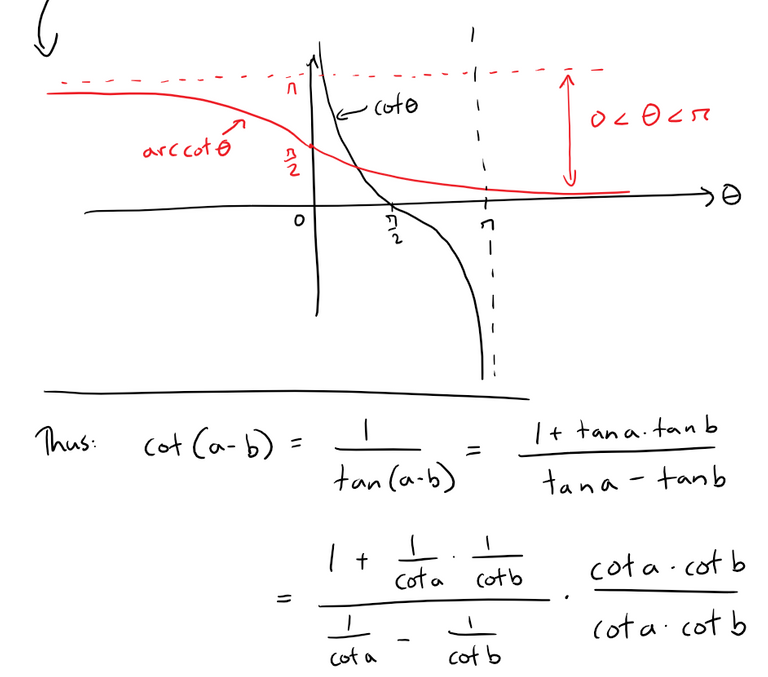
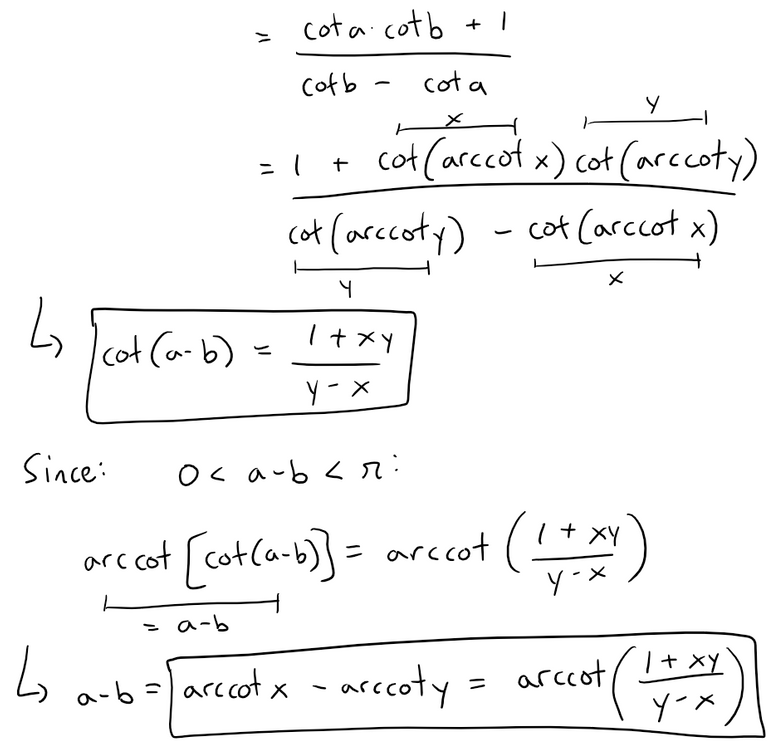
Solution to (b):
We can reformulate the polynomial inside arccot to match our identity from part (a).

This setup is the familiar case which gives us a telescoping series with n-th partial sum:
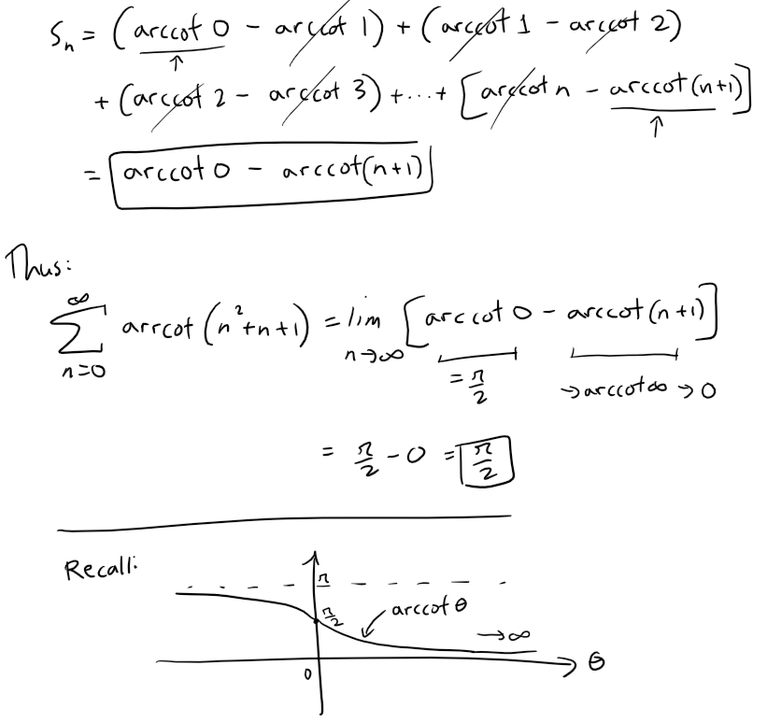
Problem 9
Find the interval of convergence of the following series and find its sum.
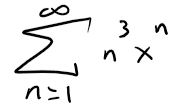
Solution:
We can start with the following geometric series and differentiate:
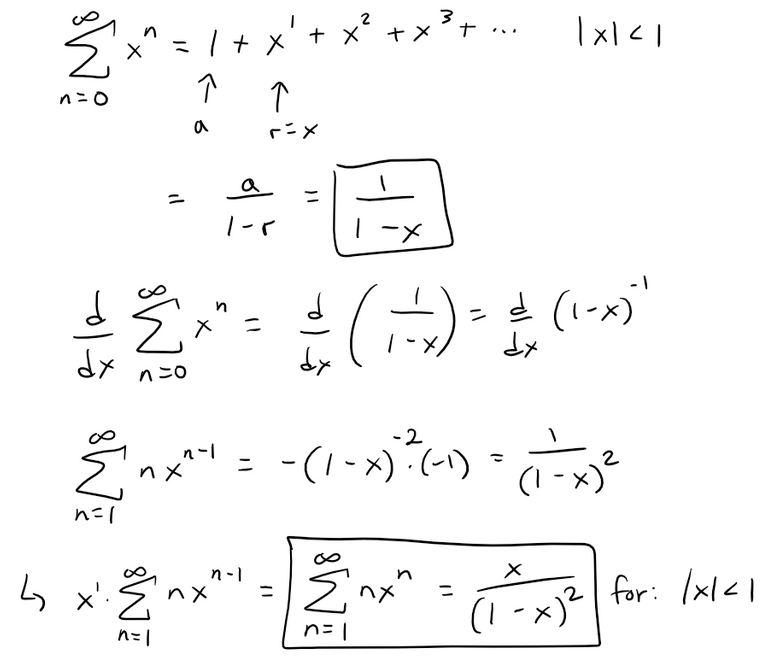
Differentiating again, this time using the quotient rule, we have:
Retrieved: 22 August 2022
Archive of notes: https://archive.ph/wip/MWVaN
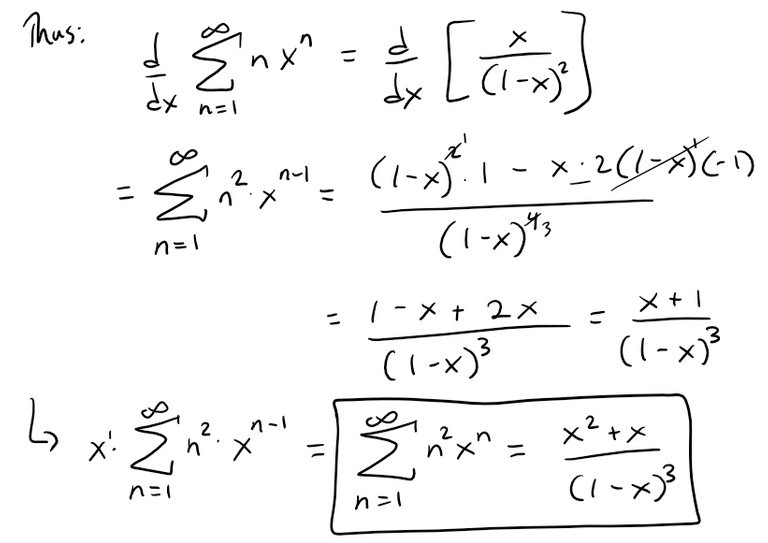
Differentiating one last time:

The radius of convergence is 1 because that is the radius of convergence for the geometric series we started with.
A geometric series is also a form of a power series and the radius of convergence remains the same after differentiation or integration.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
Retrieved: 22 January 2020
Archive: https://archive.ph/P6xfY

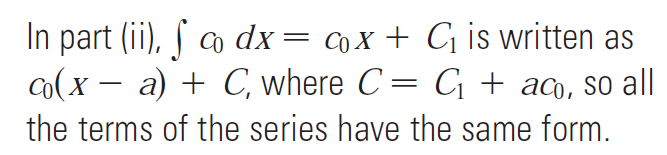
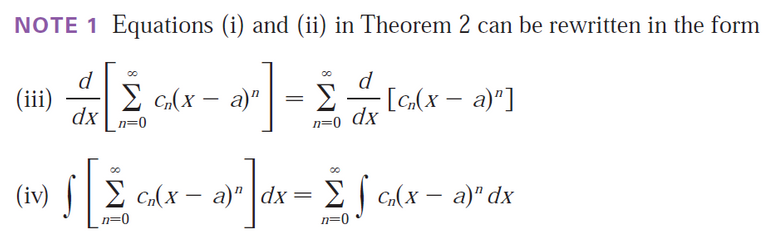
Since the radius of convergence doesn't deal with the end points, we have to determine convergence separately at the endpoints.
If x = ± 1, the series diverges by the Test for Divergence.
https://peakd.com/@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/yOKBA
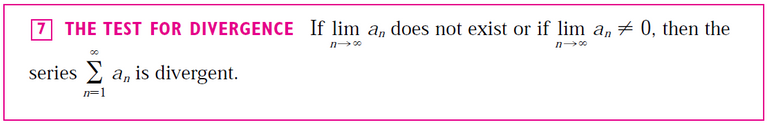

Thus, the interval of convergence is (-1, 1).
Problem 10
If:
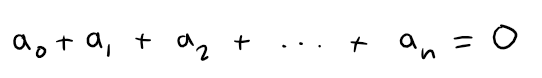
Show that:
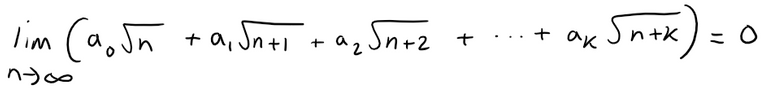
If you don't see how to prove this, try the problem-solving strategy of using analogy.
Try the special cases k = 1 and k = 2 first.
If you see how to prove the assertion for these cases, then you will probably see how to prove it in general.
Solution:
My calculus book describes the problem-solving technique of Using Analogy as follows:
Use Analogy:
Try to think of an analogous problem, that is, a similar problem, a related problem, but one that is easier than the original problem.
If you can solve the similar, simpler problem, then it might give you the clues you need to solve the original, more difficult problem.
For instance, if a problem involves very large numbers, you could first try a similar problem with smaller numbers.
Or if the problem involves three-dimensional geometry, you could look for a similar problem in two-dimensional geometry.
Or if the problem you start with is a general one, you could first try a special case.
We are hinted at trying a specific case.
Let's first try the case k = 1:

Now let's try the general case:
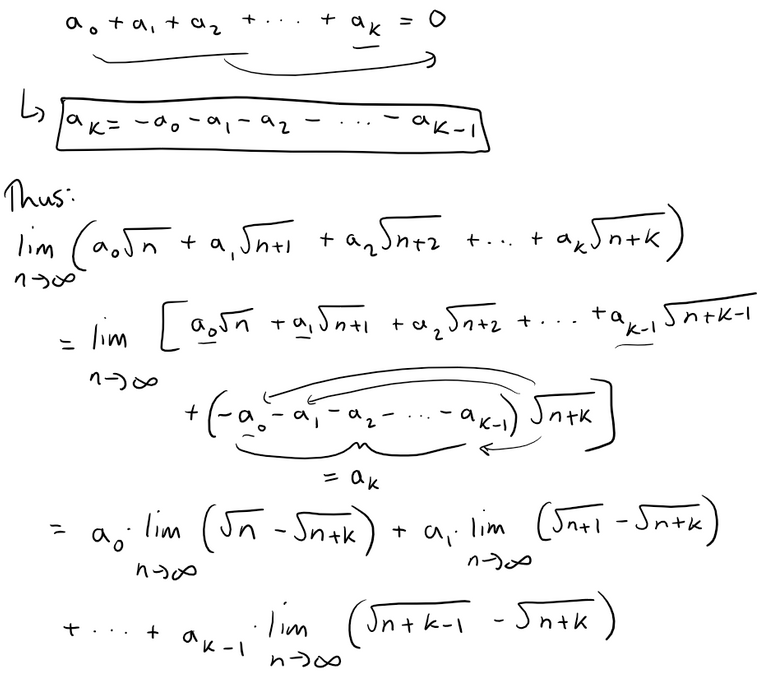
Each of these limits is 0 by the same type of simplification as in the case k = 1.
So we have:
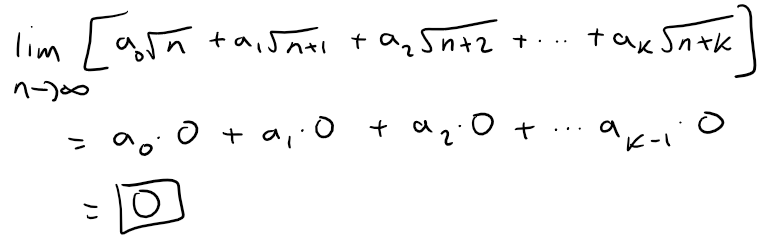
Problem 11
Find the sum of the series:
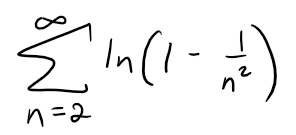
Solution:
Let's try to simplify this series.
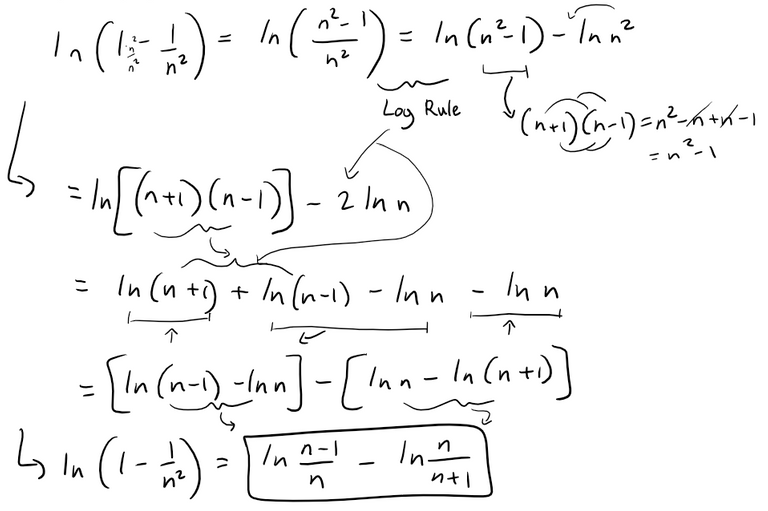
This of course looks like we can have another telescoping sum!
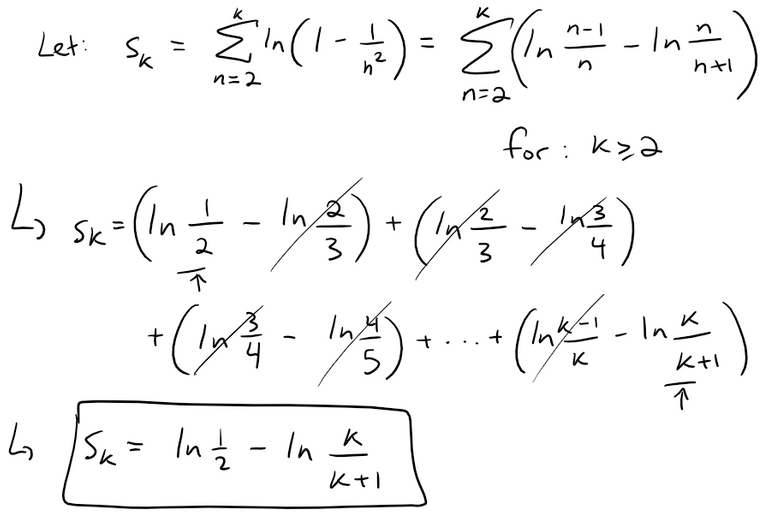
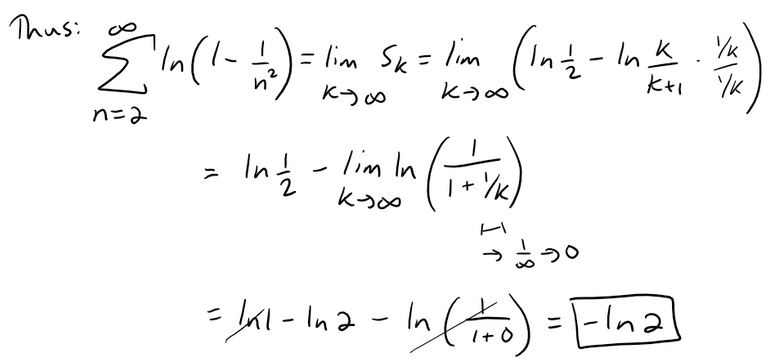
Problem 12
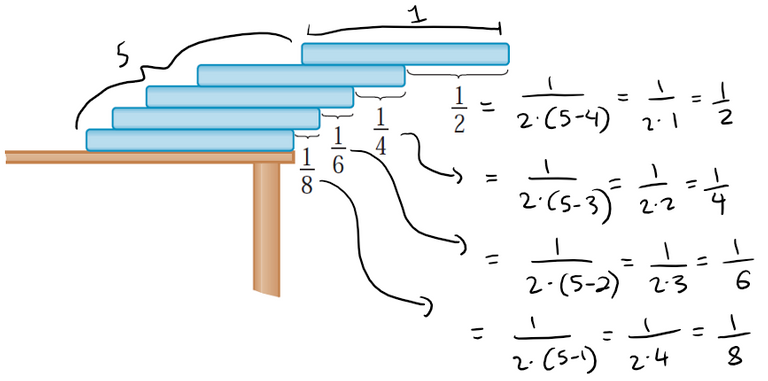
Suppose you have a large supply of books, all the same size, and you stack them at the edge of a table, with each book extending farther beyond the edge of the table than the one beneath it.
Show that it is possible to do this so that the top book extends entirely beyond the table.
In fact, show that the top book can extend any distance at all beyond the edge of the table if the stack is high enough.
Use the following method of stacking:
The top book extends half its length beyond the second book.
The second book extends a quarter of its length beyond the third.
The third extends one-sixth of its length beyond the forth, and so on.
(Try it yourself with a deck of cards.)
Consider centers of mass.

Solution:
First let's note the pattern of the distances.
Now let's place the y-axis and x-axis as shown below and let the length of each book be L.
The center of mass (COM) is represented with a dot and n is the total number of books.
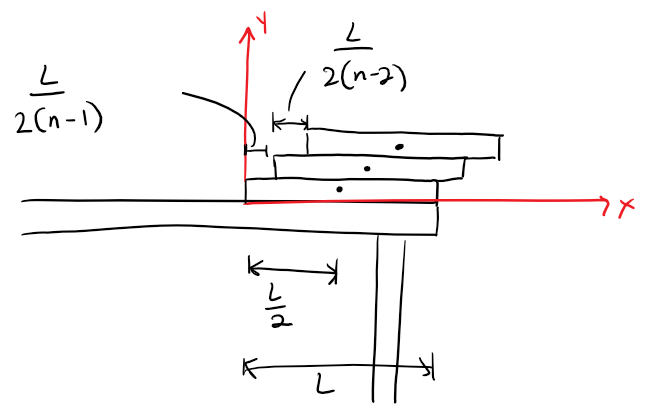
We want to show that the center of mass of the system of n books lies above the table, that is x̄ < L.
Note that x̄ is called "x bar" and represents the weighted average center of mass of the system.
The x-coordinates of the centers of mass of the books are:
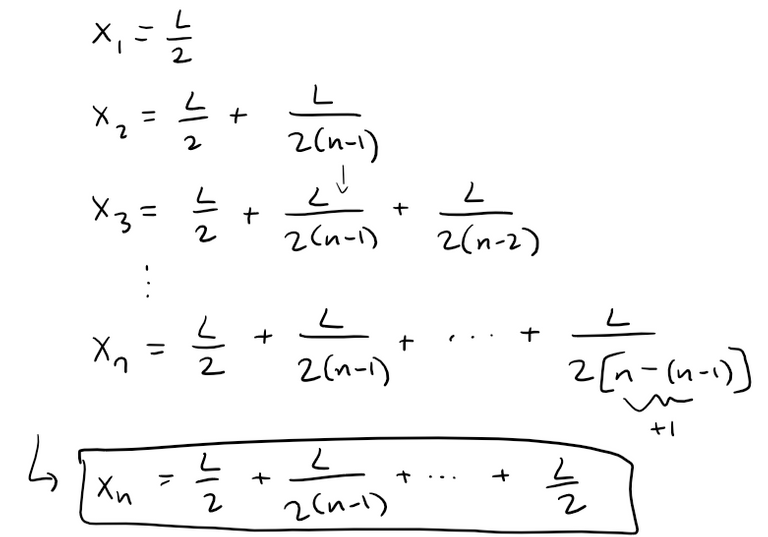
Each book has the same mass m, so if there are n books, then:
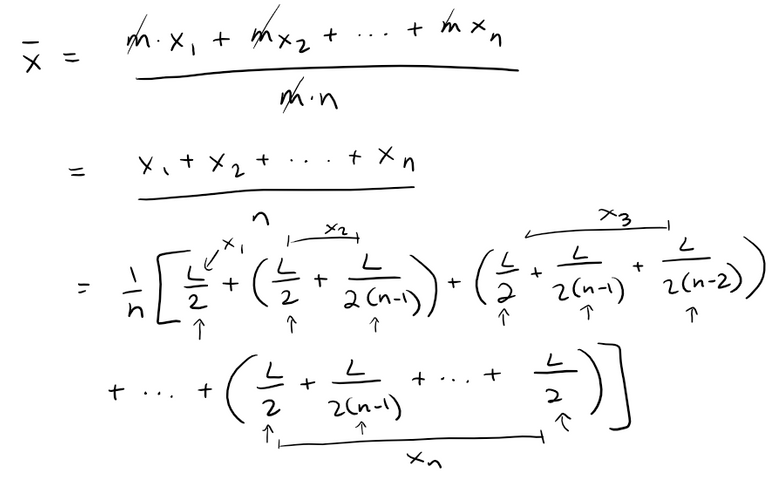

This shows that, no matter how many books are added according to the given scheme, the center of mass lies above the table.
It remains to observe that the following series is divergent (harmonic series):
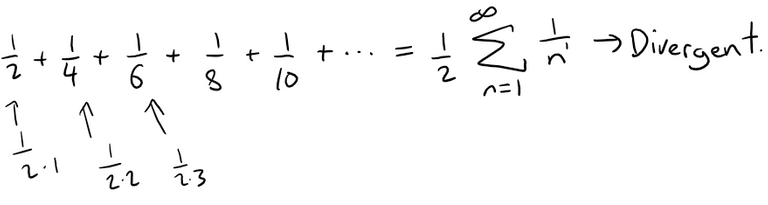
Recall that the harmonic series is a divergent p-series where p = 1.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-integral-test-and-estimate-of-sums
Retrieved: 23 August 2022
Archive: https://archive.ph/wip/6xUDW
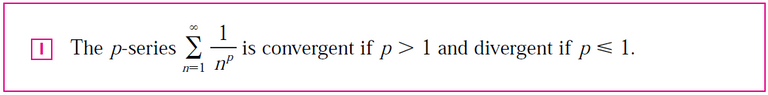
Thus we can make the top book extend as far as we like beyond the edge of the table if we add enough books.
Problem 13
If the curve below is rotated about the x-axis, the resulting solid looks like an infinite decreasing string of beads.
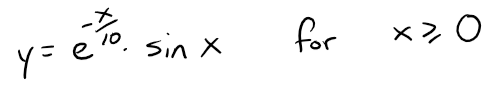
(a) Find the exact volume of the n-th bead.
(Use either a table of integrals or a computer algebra system.)
(b) Find the total volume of the beads.
Solution to (a):
Let's first graph it out.
https://www.desmos.com/calculator/frdvpc4mig
Retrieved: 23 August 2022
Archive: https://archive.ph/wip/tsHp6
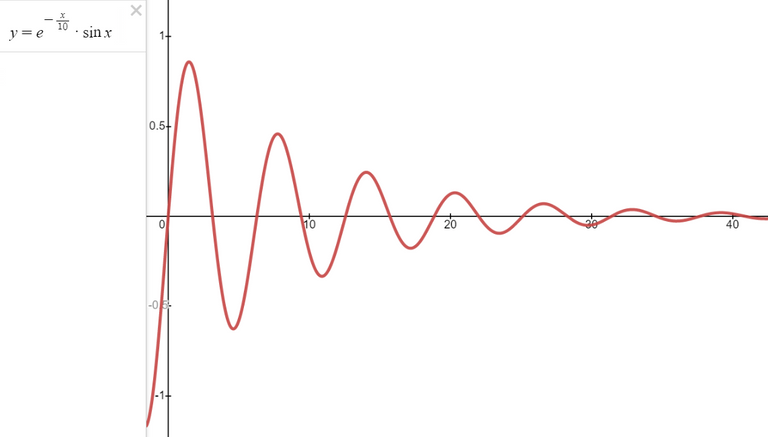
If we rotated the curve about the x-axis, we can graph the resulting shape using the amazing GeoGebra 3D calculator by representing the curve as the radius of a circle.
https://www.geogebra.org/m/kPNmmHgj
Retrieved: 23 August 2022
Archive: https://archive.ph/wip/E0Vpa
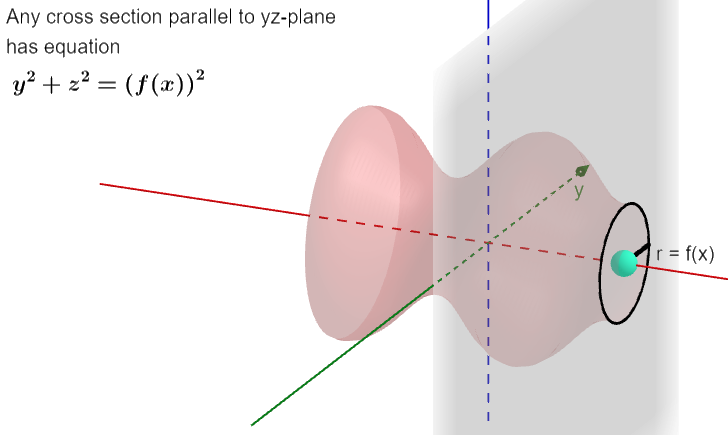
Solving for z we get two square roots which correspond to a 3D surface.
https://www.geogebra.org/calculator/cy2rygjh
Retrieved: 23 August 2022
Archive: https://archive.ph/wip/JM1AE
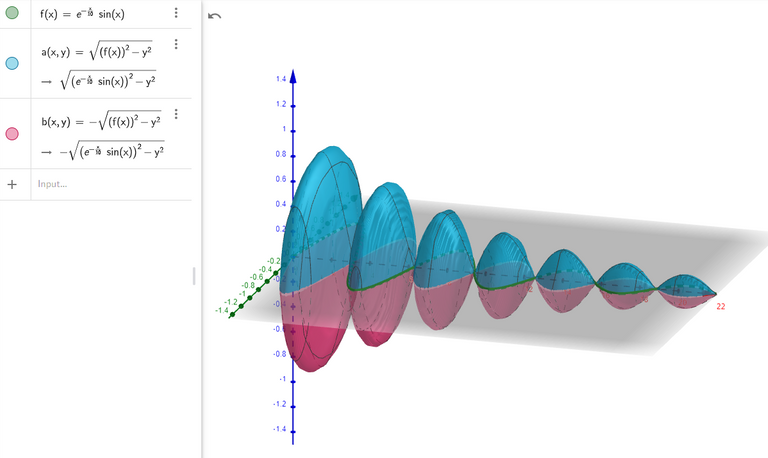
As we can see above, the solid looks an infinite decreasing string of beads.
Now, let's determine the volume of the n-th bead.
The x-intercepts of the curve occur where sin x = 0:
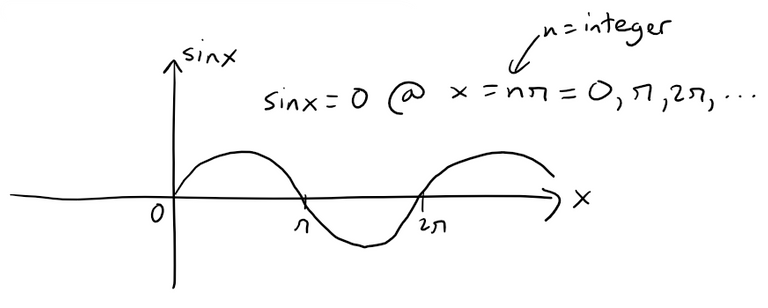
Thus, recalling the formula for disks, we have:

We can now use the computer algebra system (CAS) from Integral-Calculator.com:
https://www.integral-calculator.com/...
Retrieved: 23 August 2022
Archive: Not available
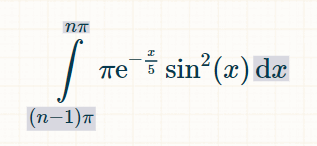
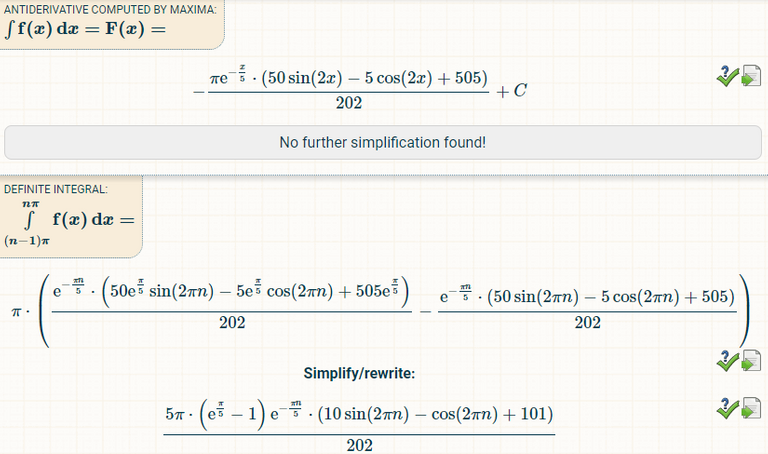
We can simplify the resulting formula:
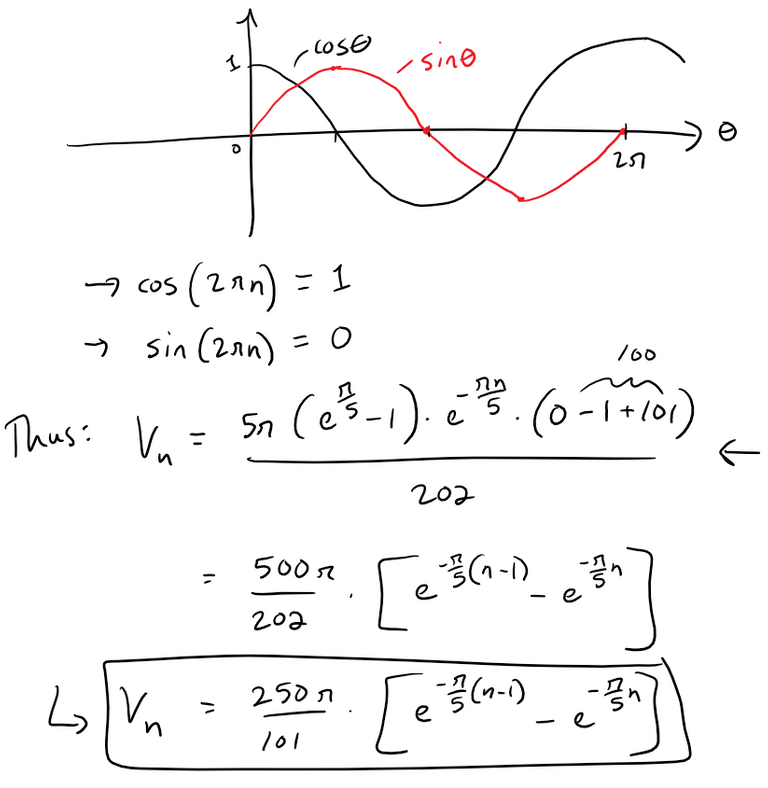
Solution to (b): Method 1: Telescoping Sum
The total volume is, using none other than the telescoping sum:

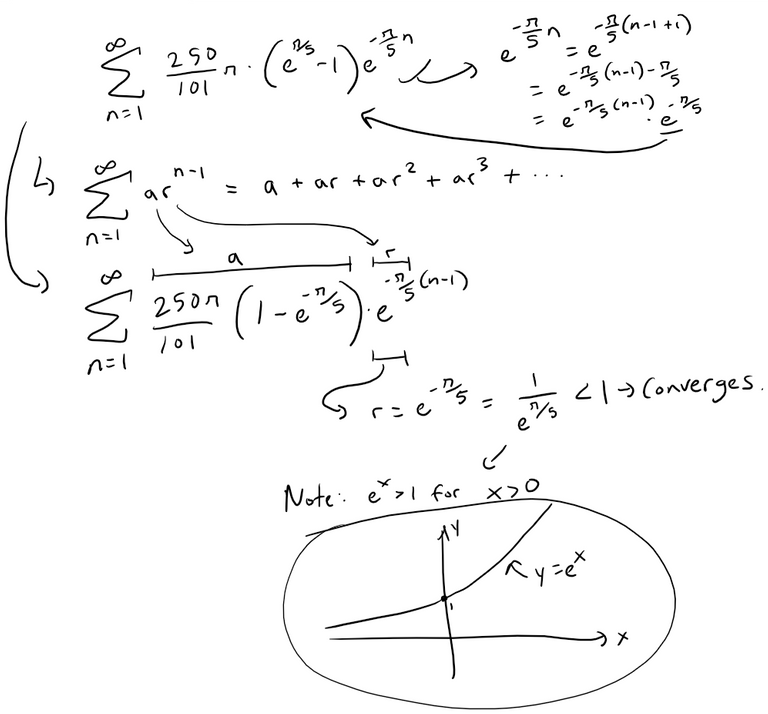
Solution to (b): Method 2: Geometric Series
If we start off by using the volume in part (a) at the start of our simplification, we can notice a geometric series.
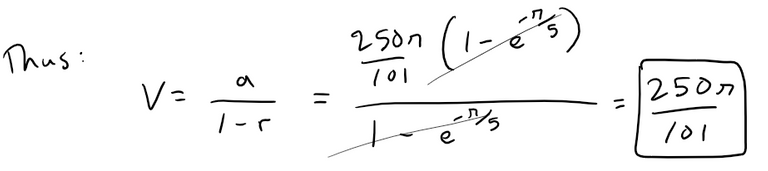
Problem 14
If p > 1, evaluate the expression:

Solution:
First notice that both series are absolutely convergent (p-series with p > 1) and therefore convergent.
https://peakd.com/@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests
Retrieved: 22 August 2022
Archive: https://archive.ph/wip/tbgDI


Let the given expression be called x. Then:
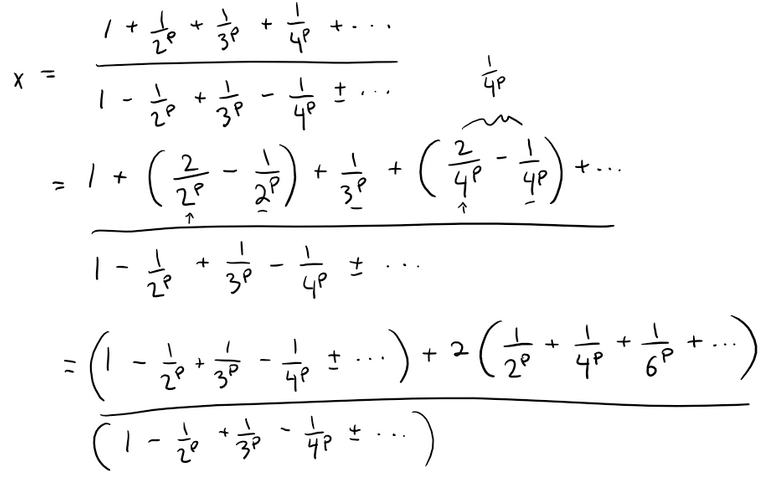

Problem 15
Suppose that circles of equal diameter are packed tightly in n rows inside an equilateral triangle.
The figure illustrates the case n = 4.
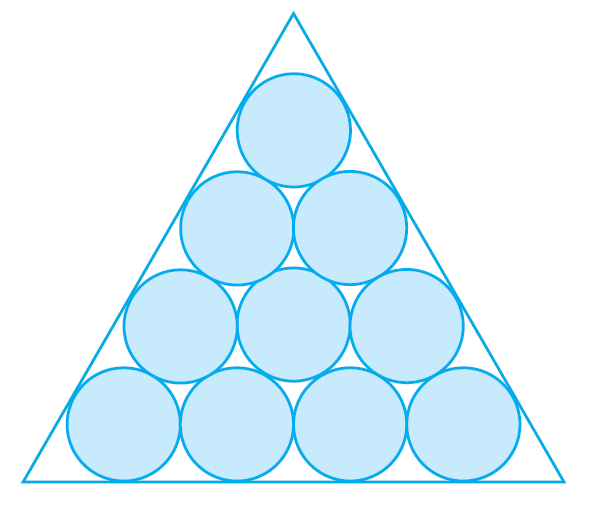
If A is the area of the triangle and An is the total area occupied by the n rows of circles, show that:
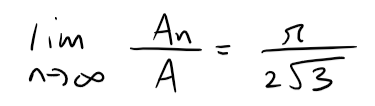
Solution:
If L is the length of a side of the equilateral triangle, then the area is:
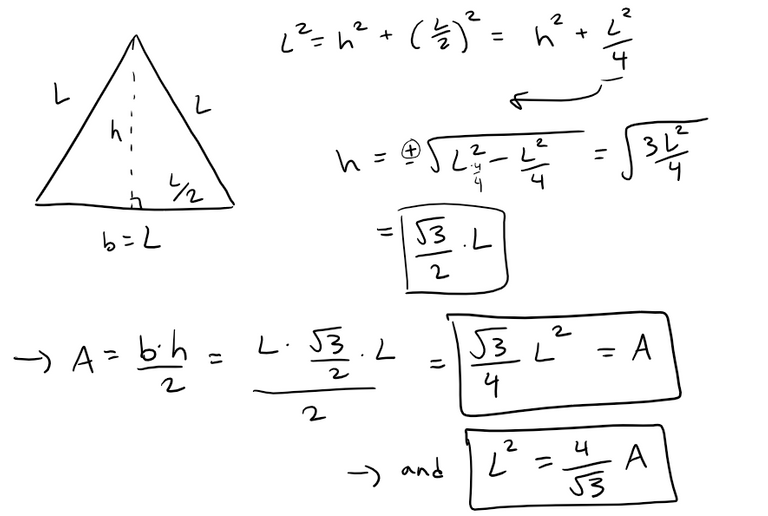
Let r be the radius of one of the circles.
When there are n rows of circles, the figure shows that:
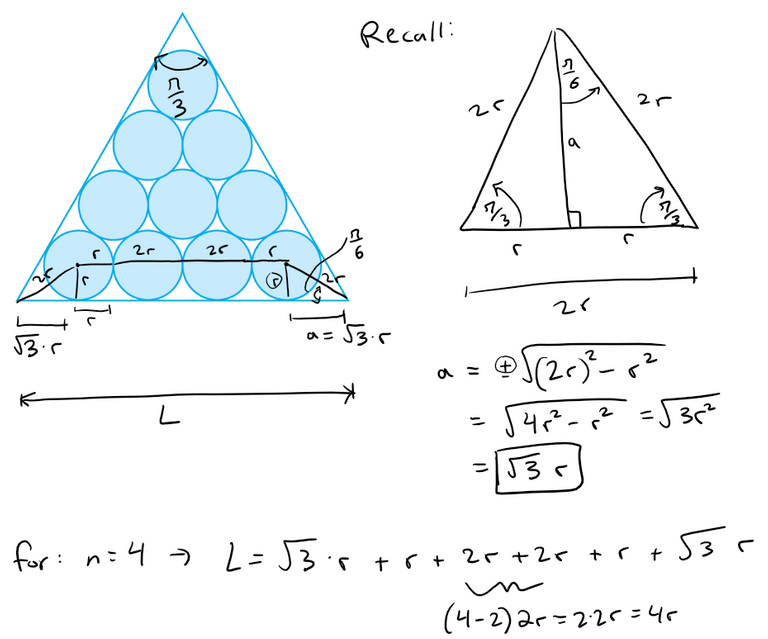

The number of circles is:

Recall that the above formula is for the sum of positive integers which I went over in my earlier video.
Retrieved: 23 August 2022
Video notes archive: https://archive.ph/wip/BhL0s

Thus the total area of the circles is:

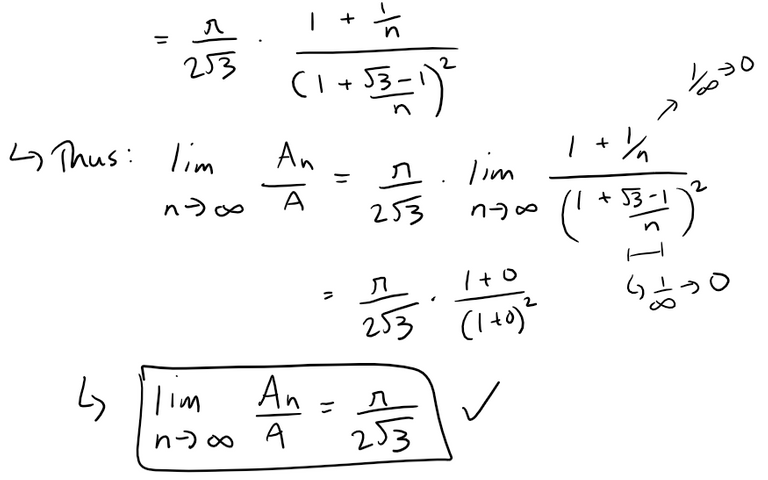
Problem 16
A sequence {an} is defined recursively by the equations:
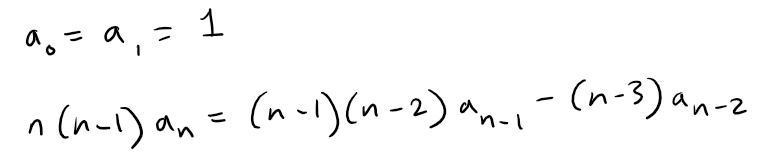
Find the sum of the series:
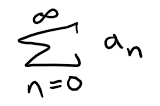
Solution:
Given the above, we can calculate the next few terms of the sequence:
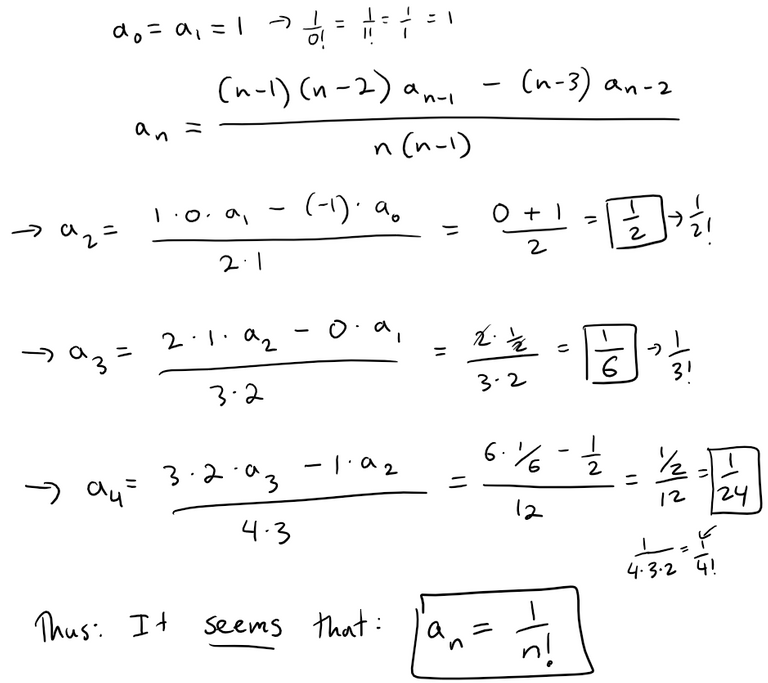
To confirm the pattern, we can use induction.
https://peakd.com/hive-128780/@mes/problems-plus-example-4-mathematical-induction
Retrieved: 23 August 2022
Archive: https://archive.ph/wip/gHATr

The first step is already done, so assume ak and ak-1 are true and solve for ak+1.

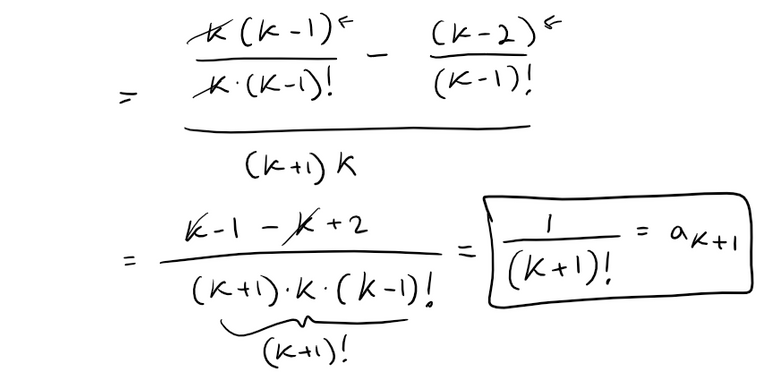
Thus the induction is complete.
This means that our series is equal to e, as per our earlier Maclaurin series table with ex = e1.
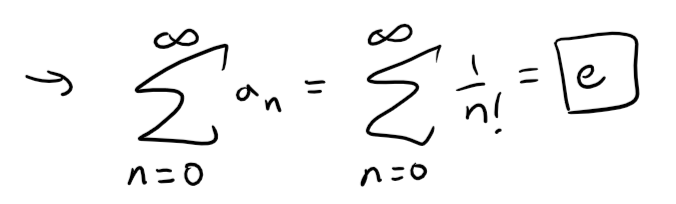
Problem 17
Taking the value of xx at 0 to be 1 and integrating a series term by term, show that:
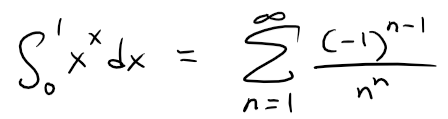
Solution:
As in my earlier video on representing functions as power series, we will have to integrate the function xx by integrating series.
We can rewrite xx by using the Maclaurin series for ex, from the earlier table above.
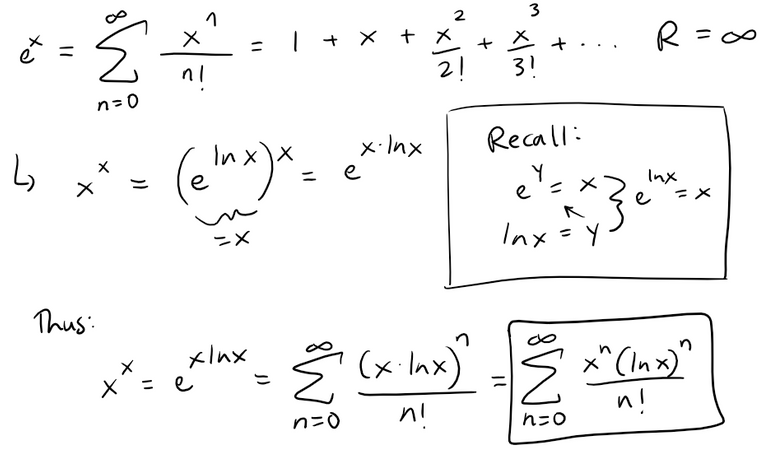
As with power series, we can integrate this series term-by-term:
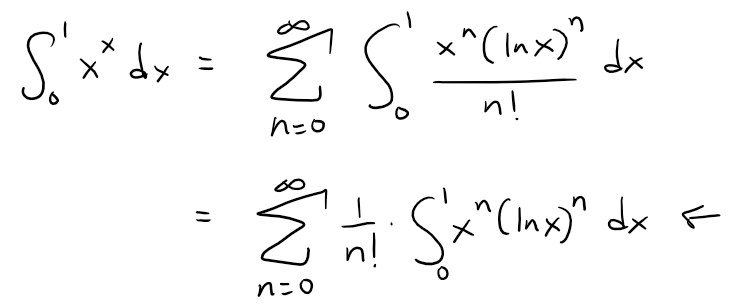

We can now apply the integration by parts, as per my earlier video.
https://peakd.com/mathematics/@mes/integration-by-parts-proof
Retrieved: 22 February 2022
Archive: https://archive.ph/wip/cOjtq
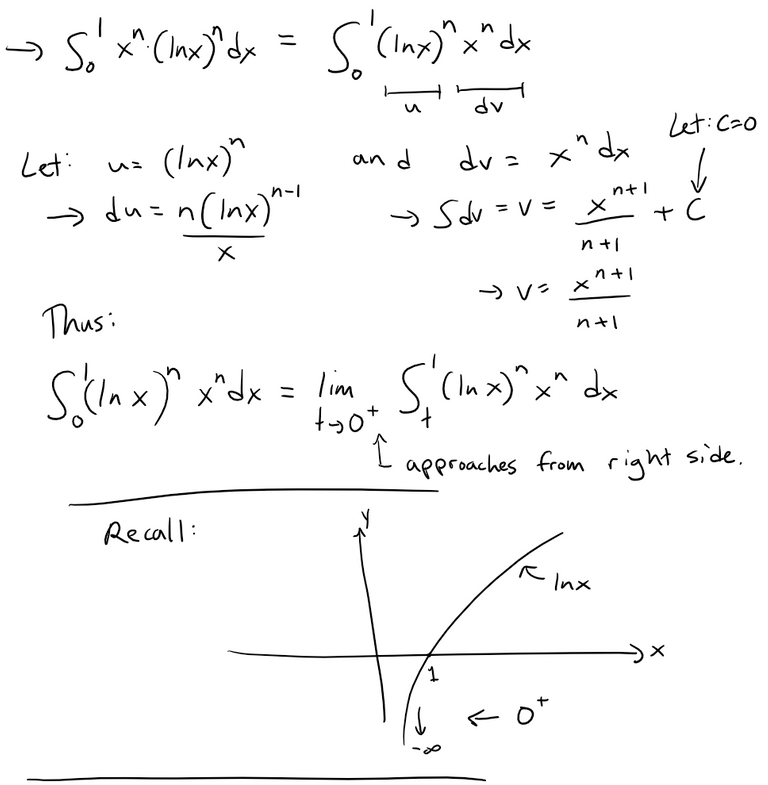
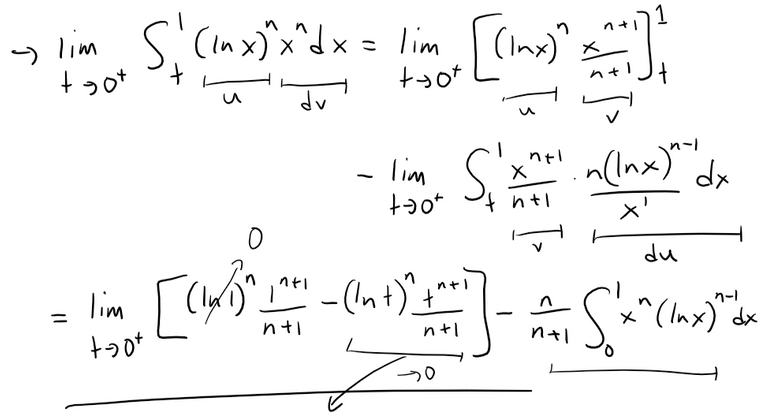
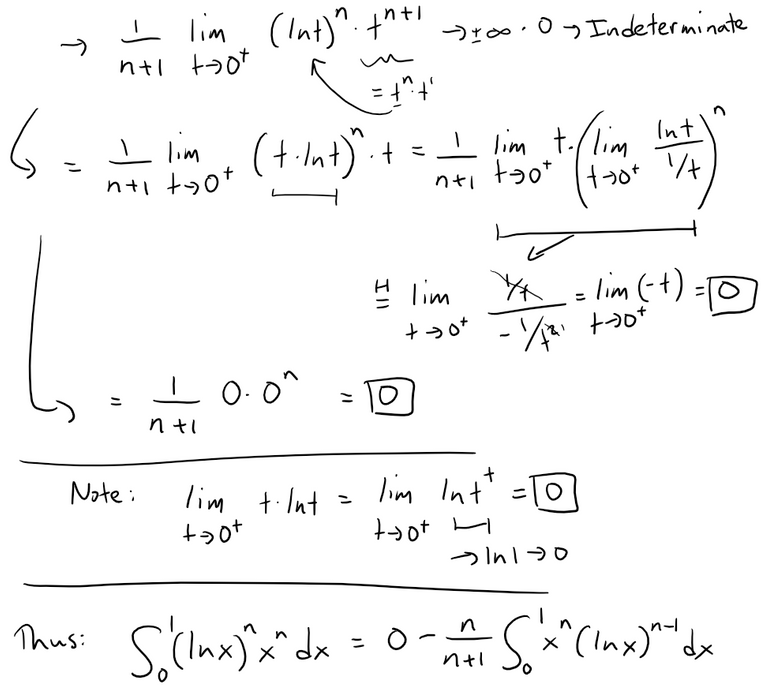
If we repeat the integration by parts, we can see a pattern.
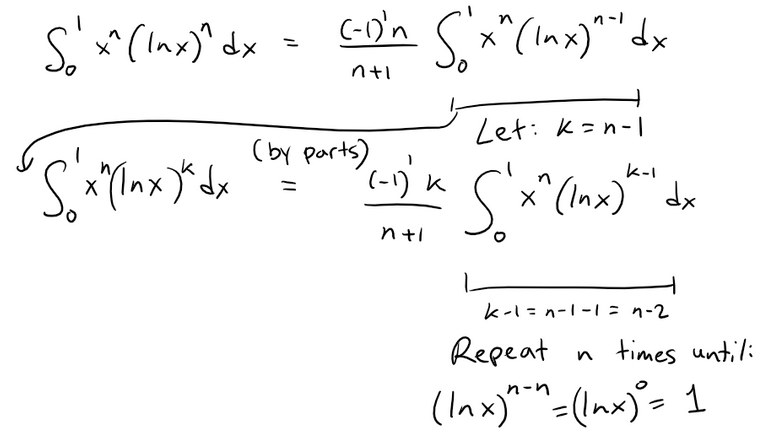
Thus combining these steps we get:
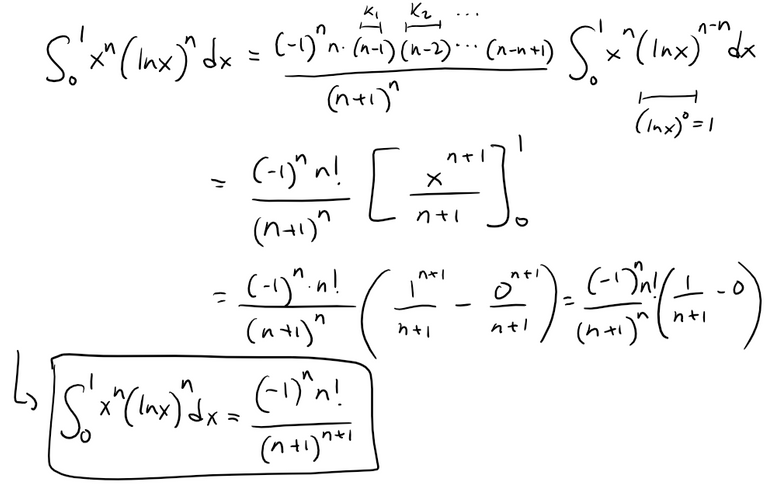
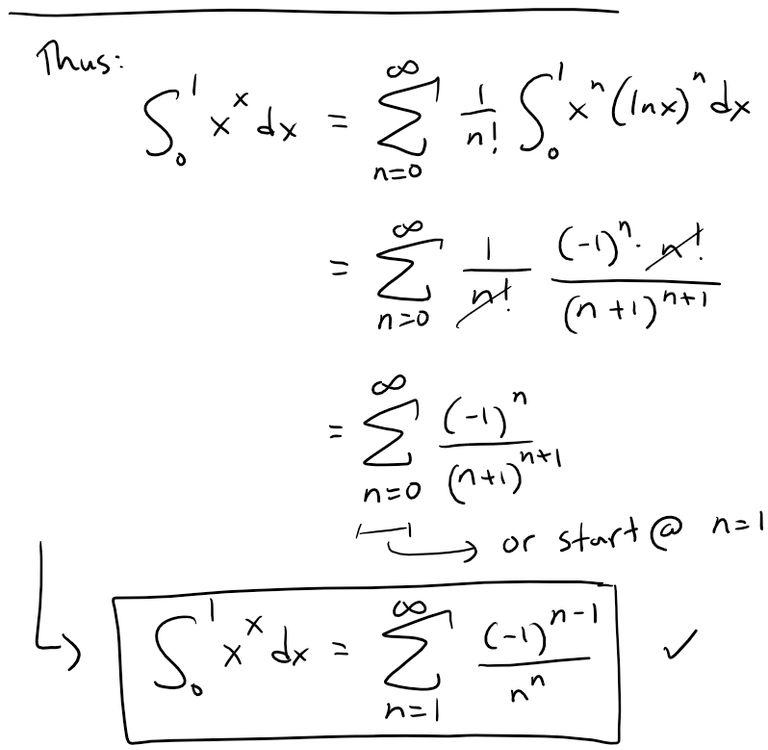
Problem 18
Starting with the vertices P1(0, 1), P2(1, 1), P3(1, 0), P4(0, 0) of a square, we construct further points as shown in the figure:
P5 is the midpoint of P1P2.
P6 is the midpoint of P2P3.
P7 is the midpoint of P3P4 and so on.
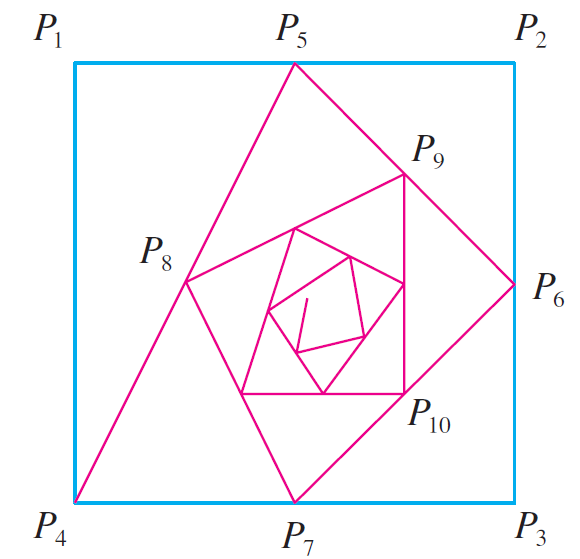
The polygonal spiral path P1P2P3P4P5P6P7… approaches a point P inside the square.
(a) If the coordinates of Pn are (xn, yn), show that:
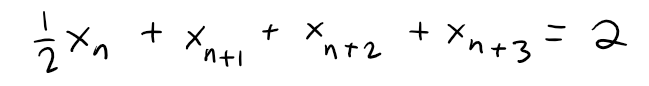
and find a similar equation for the y-coordinates.
(b) Find the coordinates of P.
Solution to (a):
Since Pn is defined as the midpoint of Pn-4Pn-3, we have:
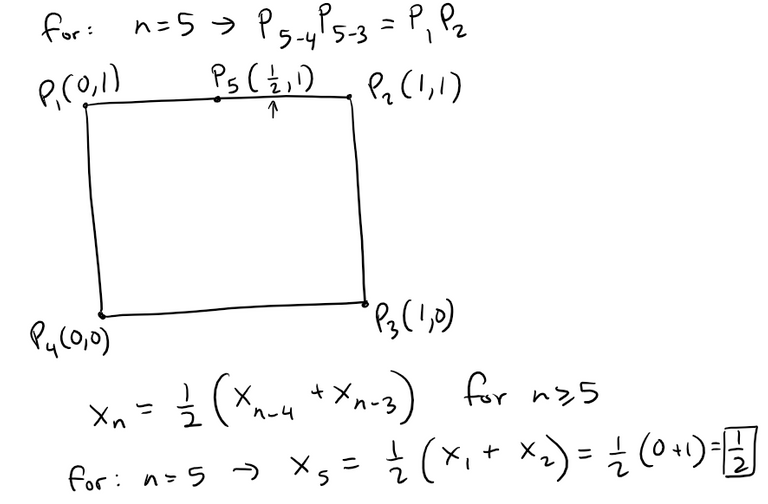
Using induction we can prove that:
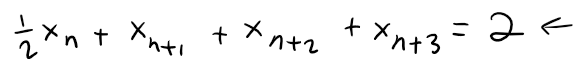
The case n = 1 is immediate, since:
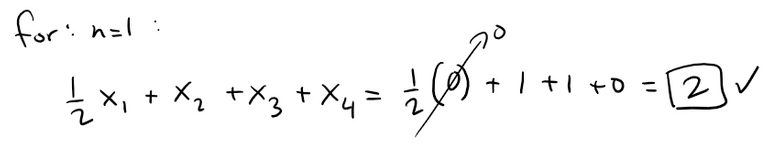
Assume that the result holds for n = k - 1 and then solve for the case n = k.

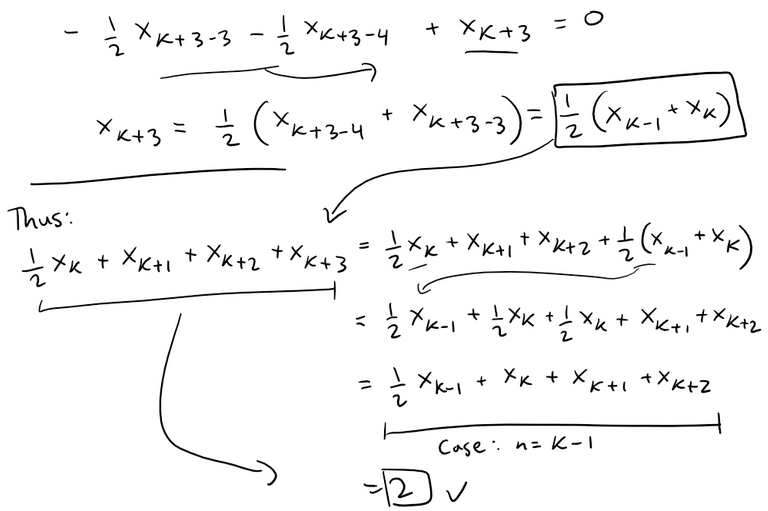
Thus our induction hypothesis is true.
Similarly, the same argument holds true for y except 2 is replaced by:
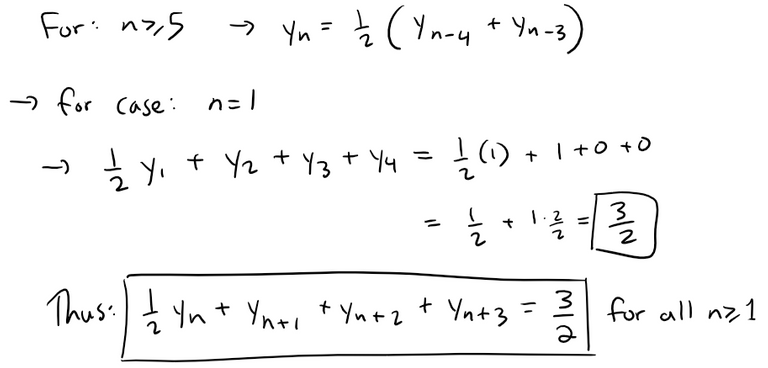
Solution to (b):
We are asked to find the coordinates of P.
We can take the following limit and solve for xn:

Problem 19
Find the sum of the series:
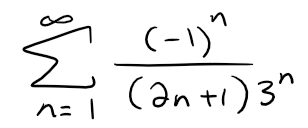
Solution:
From the earlier table, the Maclaurin series for tan-1(x) is:
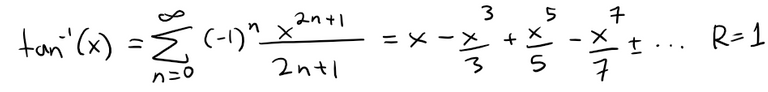
In particular, notice that:
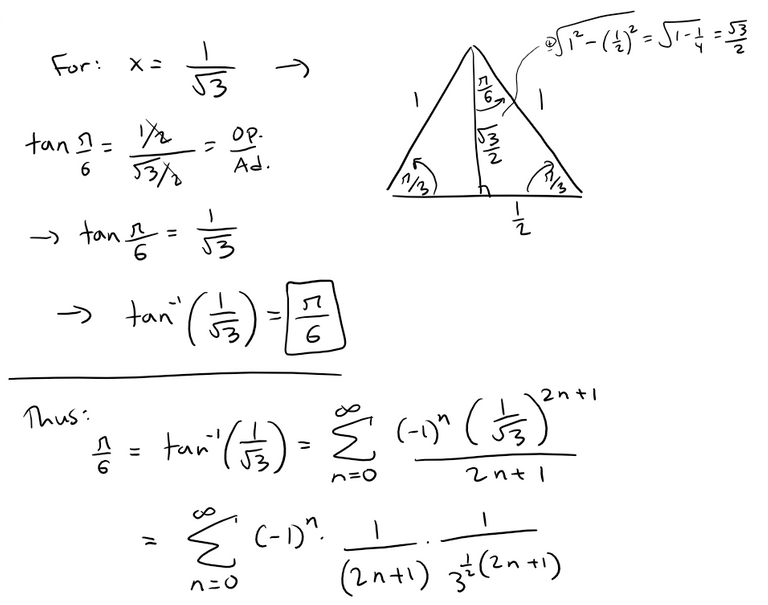

Problem 20
Carry out the following steps to show that:
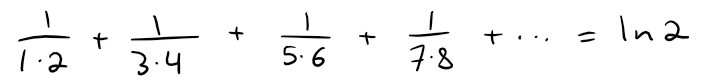
(a) Use the formula for the sum of a finite geometric series to get an expression for:

(b) Integrate the result of part (a) from 0 to 1 to get an expression as an integral for:

(c) Deduce from part (b) that:
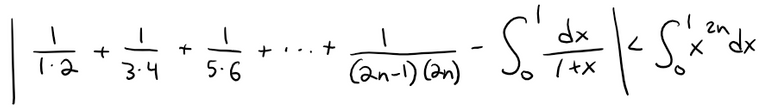
(d) Use part (c) to show that the sum of the given series is ln 2.
Solution to (a)
Recall the sum of the a finite geometric series.
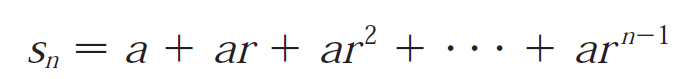
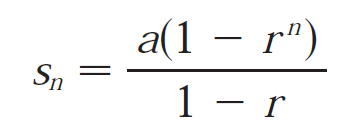
In our case we have:

Solution to (b):
Integrating the result from part (a) from 0 to 1 we get:

Solution to (c):
Notice the following:
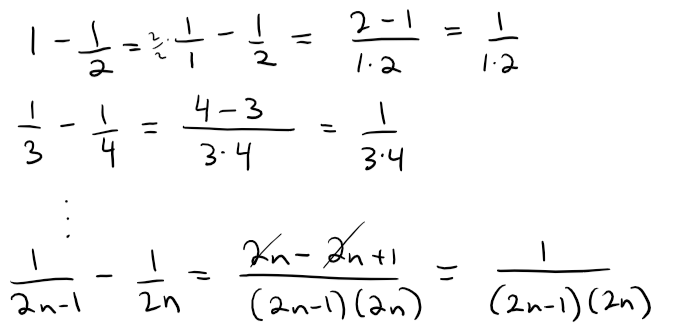
Thus we see from part (b) that:

Solution to (d):
Note that:
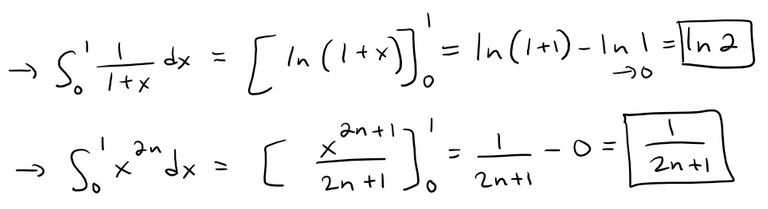
Thus part (c) becomes:
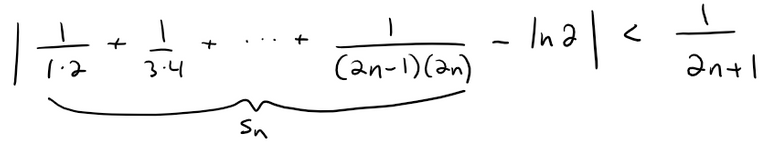
In other words, the n-partial sum sn of the given series satisfies:
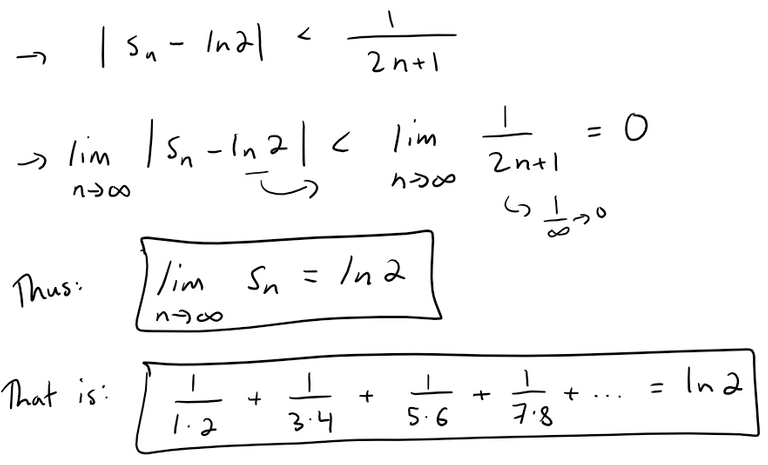
Problem 21
Find all the solutions of the equation:
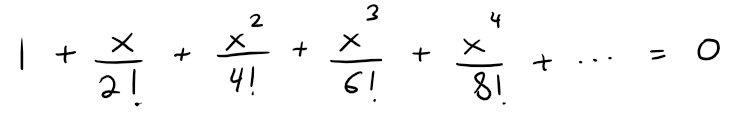
Hint: Consider the cases x ≥ 0 and x < 0 separately.
Solution:
Let f(x) denote the left side of the given equation.
If x ≥ 0 then f(x) ≥ 1 and there are no solutions of the equation.
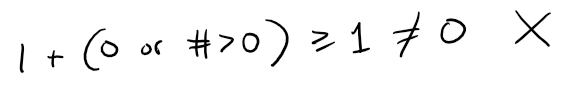
Note that f(-x2) is equal to the Maclaurin series for cos x.
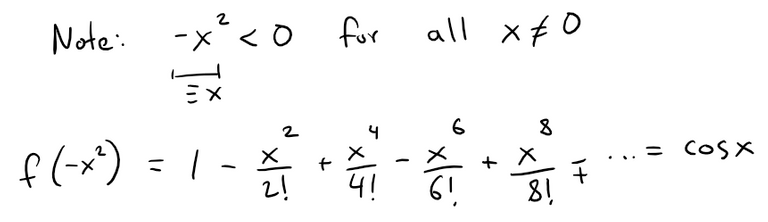
The solutions of cos x = 0 for -x2 < 0 are given by:
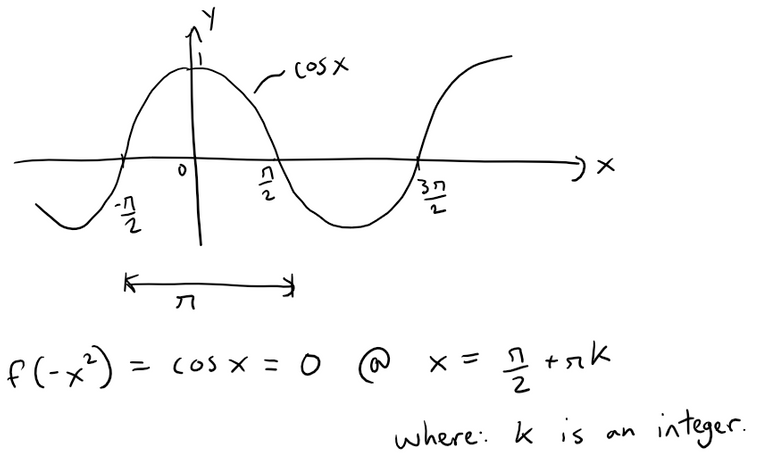
Thus the solutions for f(x) = 0 are:
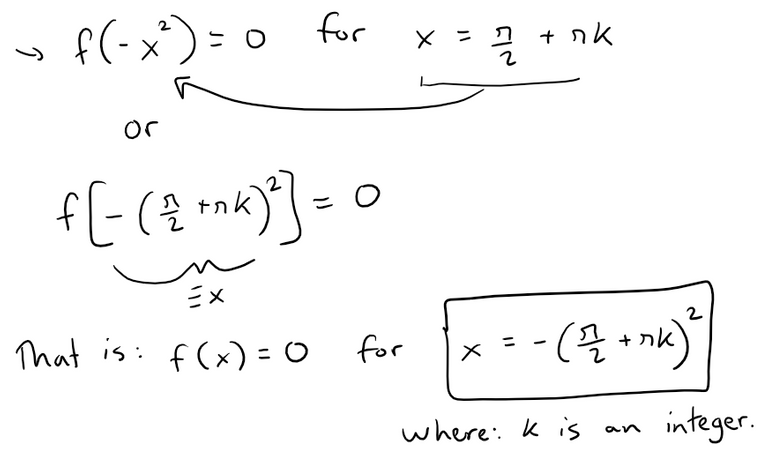
Note that I deviated from the solutions manual because it assumed that x < 0 even after it was transformed to -x2. That is, they considered cos(x) = 0 for x < 0. This does not necessarily always have to be the case because if x > 0, the transformation is still -x2 < 0.
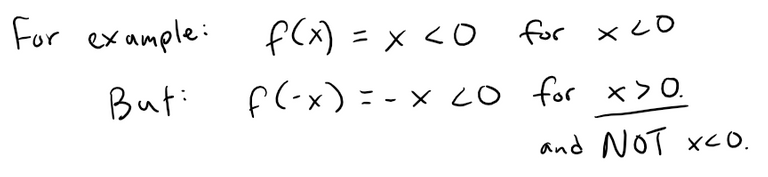
Problem 22
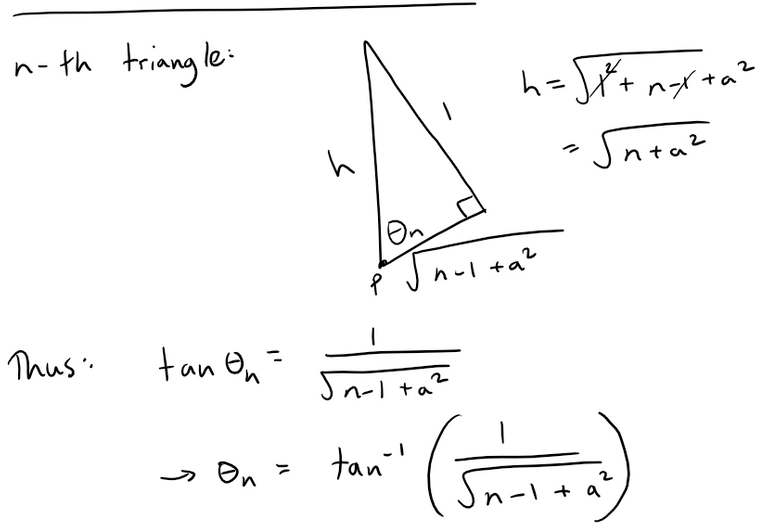
Right-angled triangles are constructed as in the figure.
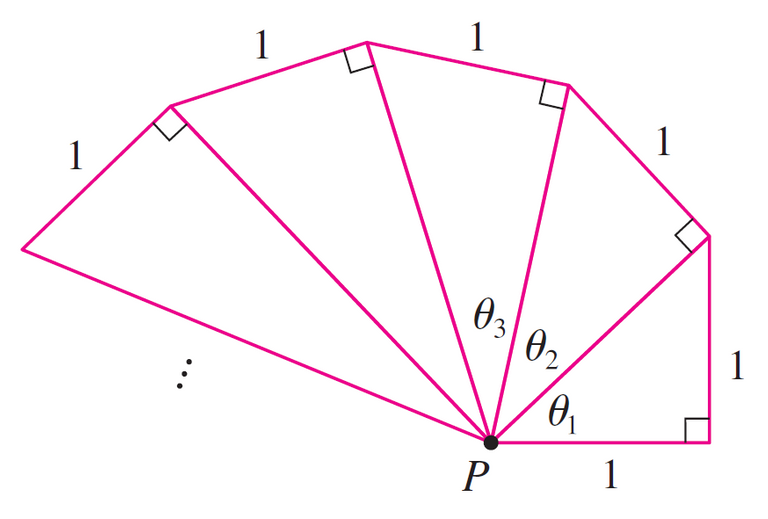
Each triangle has height 1 and its base is the hypotenuse of the preceding triangle.
Show that this sequence of triangles makes indefinitely many turns around P by showing that ∑θn is a divergent series.
Solution:
Suppose that the base of the first triangle has length a.
Then by repeated use of the Pythagorean theorem, we find that the bases of the successive right triangle are:
Thus we wish to show that the following series diverges:
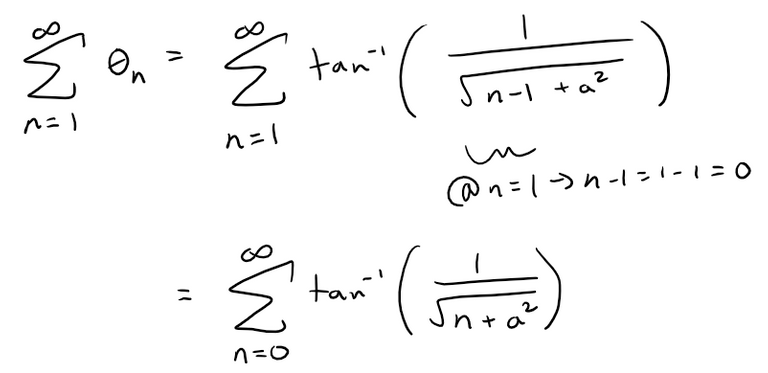
First notice that the following series diverges by Limit Comparison Test:
https://peakd.com/@mes/infinite-sequences-and-series-the-comparison-tests
Retrieved: 24 August 2022
Archive: https://archive.ph/wip/69yXp
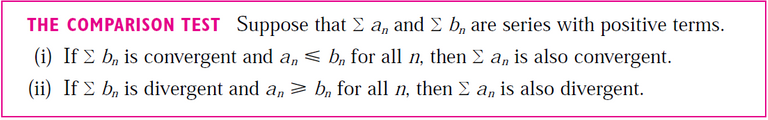
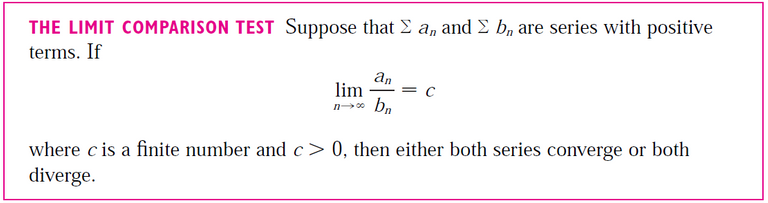

Now we can apply the Limit Comparison Test again but this time with our original series.

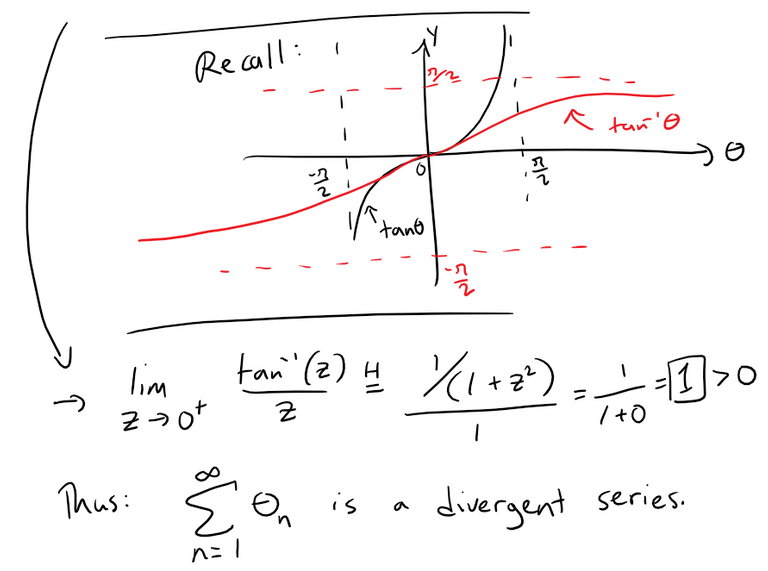
Recall the derivative of tan-1(x) from my earlier video:
Retrieved: 30 August 2022
Archive of video notes: https://archive.ph/wip/r3xwa
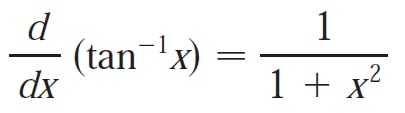
Problem 23
Consider the series whose terms are the reciprocals of the positive integers that can be written in base 10 notation without using the digit 0.
Show that this series is convergent and the sum is less than 90.
Solution:
Let's call this series S.
We can group the terms according to the number of digits in their denominators:

Now in group gn, since we have 9 choices for each of the n digits in the denominator, there are 9n terms.
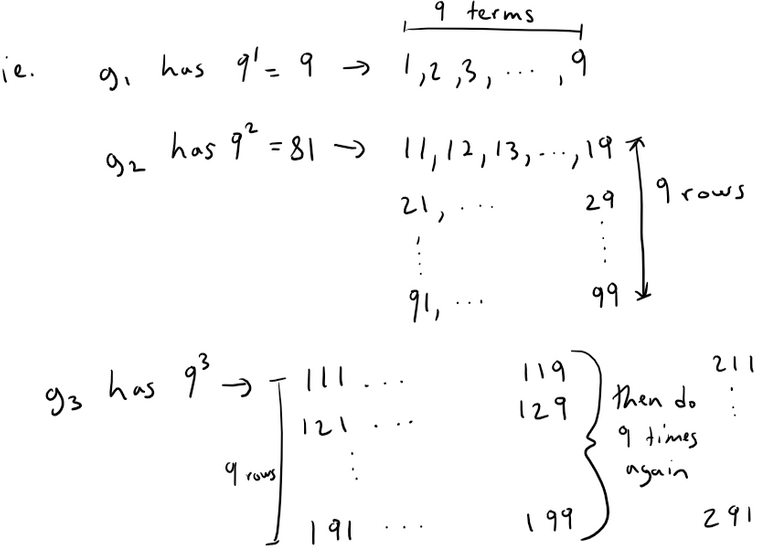
Furthermore, each term in gn is less than 1/(10n-1) except for the first term in g1.
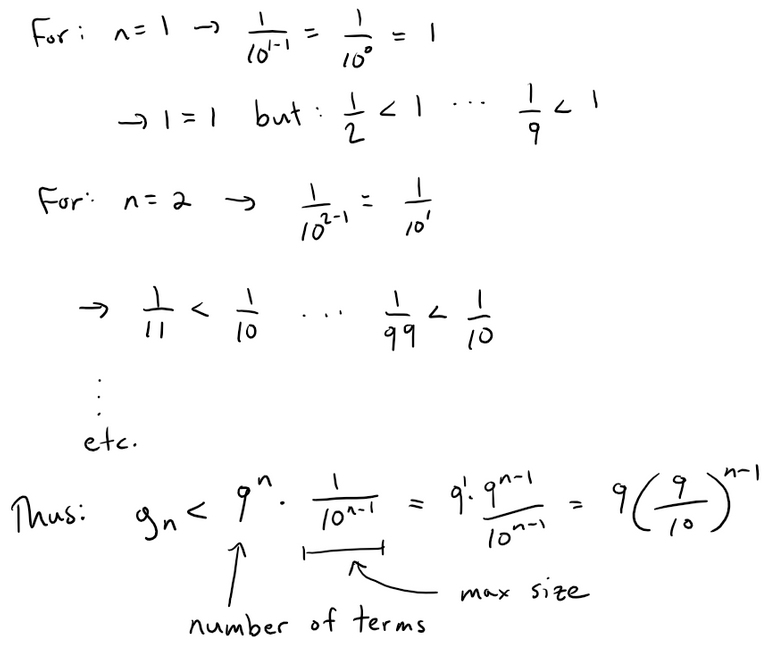
Note that S = ∑gn is less than a convergent geometric series.
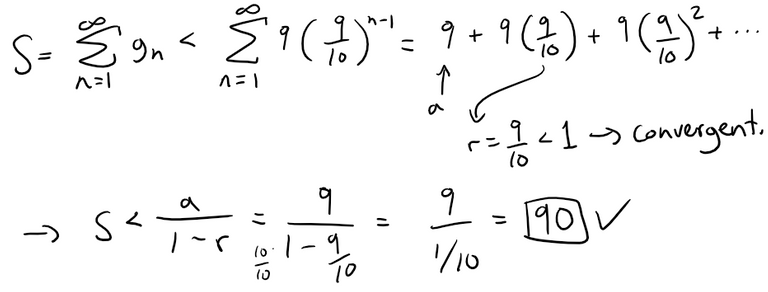
Problem 24
(a) Show that the Maclaurin series of the function:
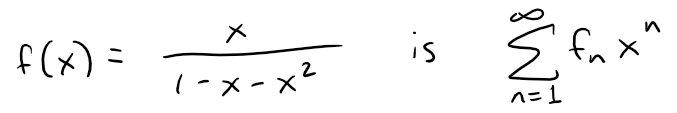
where fn is the n-th Fibonacci number, that is:
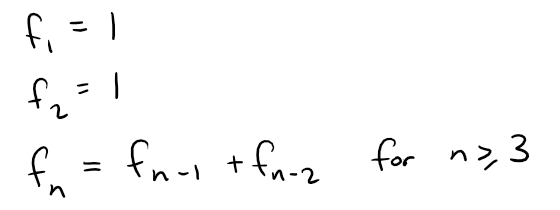
Hint: Write:

and multiply both sides of this equation by:
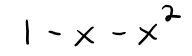
(b) By writing f(x) as a sum of partial fractions and thereby obtaining the Maclaurin series in a different way, find an explicit formula for the n-the Fibonacci number.
Solution to (a):
Let's follow the hint given.
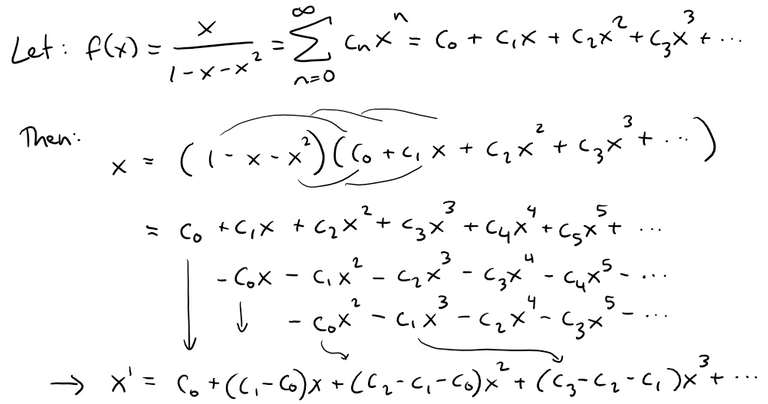
Comparing coefficients of powers of x, that is comparing the powers on the left side (x1) with the right side, gives us:
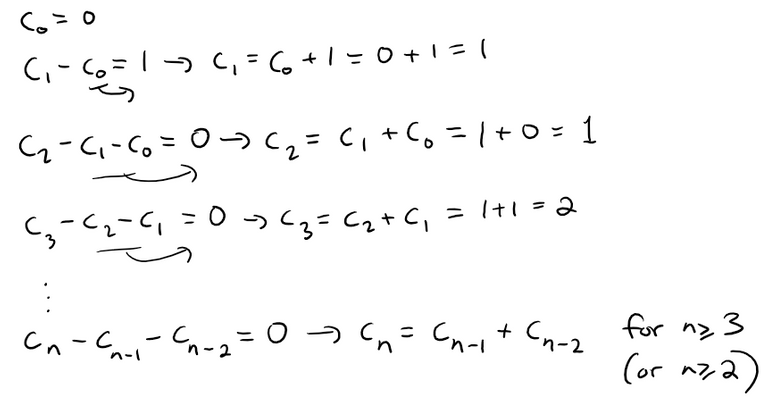
Each cn is equal to the n-th Fibonacci number, that is:
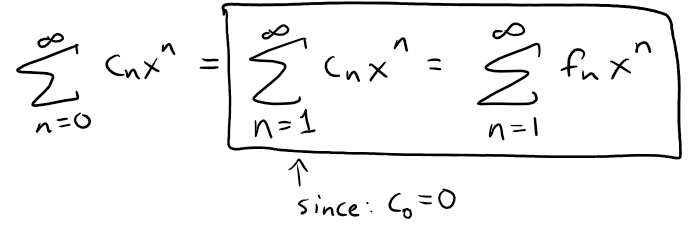
Solution to (b):
Let's start with completing the square of the following equation:

Now we can write out f(x) as:
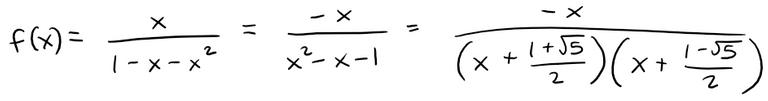
The factors in the denominator are linear, so the partial fraction decomposition is:
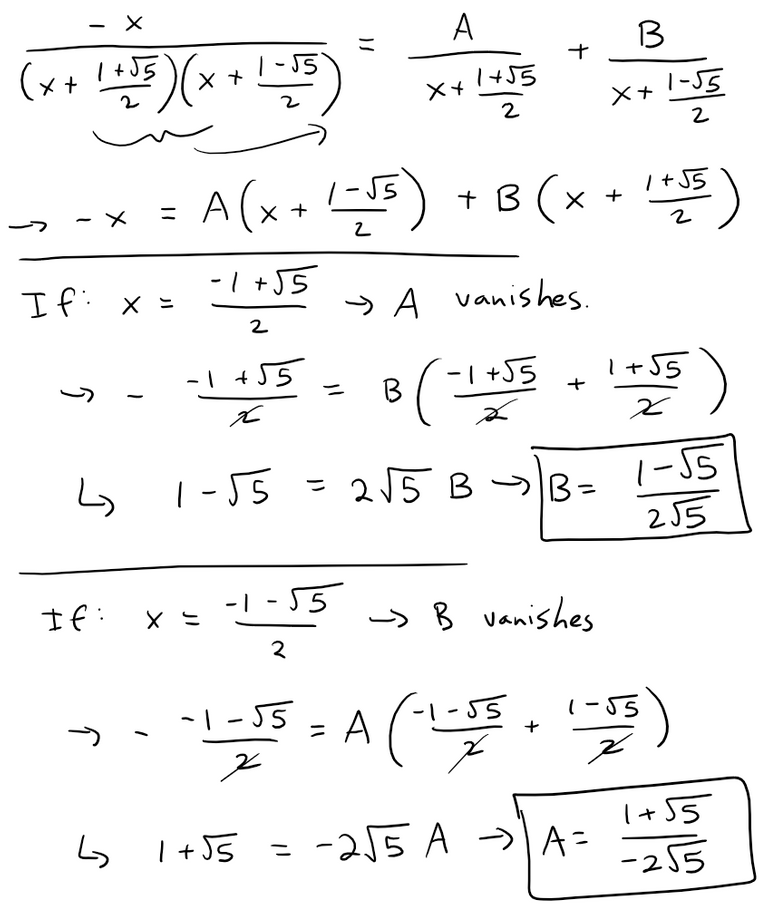

Note that the above two fractions are in the form of the sum of a convergent geometric series!
This means, we can write them each as a geometric series.
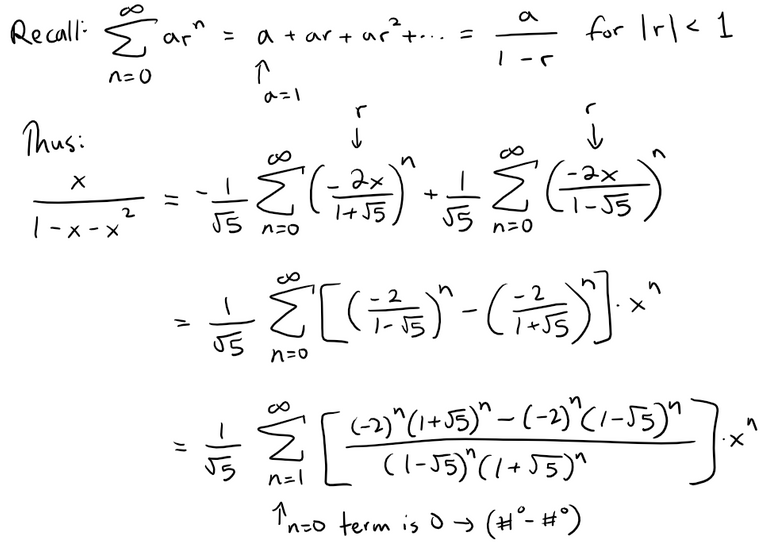
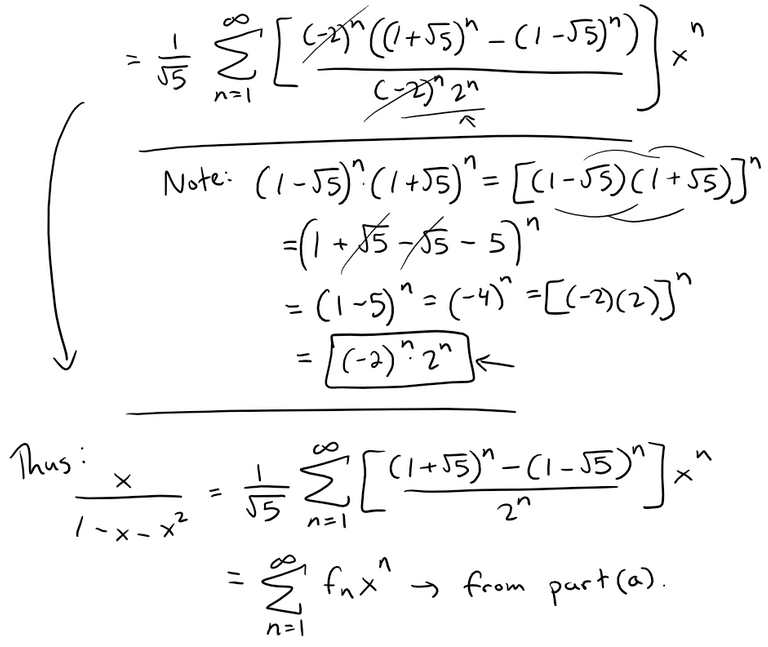
Since this series is equal to that from part (a), it means that we have an explicit formula of the n-th Fibonacci number! #Amazing
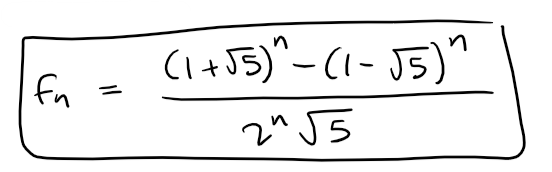
Let's do a quick calculation check:
The first 6 Fibonacci numbers are:
1
1
1+1 = 2
2+1 = 3
3+2 = 5
5+3 = 8 (f6)Calculating the 6-th Fibonacci number yields:
f6 = ((1 + sqrt(5))^6 - (1 - sqrt(5))^6)/(2^6*sqrt(5)) = 8.000000000000001 (calculator rounds during calculations).
Problem 25
Let:

Show that:
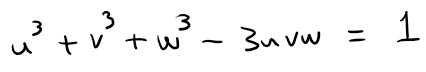
Solution:
Let's first use the Ratio Test to show that the series for u, v, and w have positive radii of convergence (so that we can do term by term differentiation):
https://peakd.com/@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests


Similarly the Ratio Test converges for v and w for all x.
Thus, we can now differentiate each of the these series.
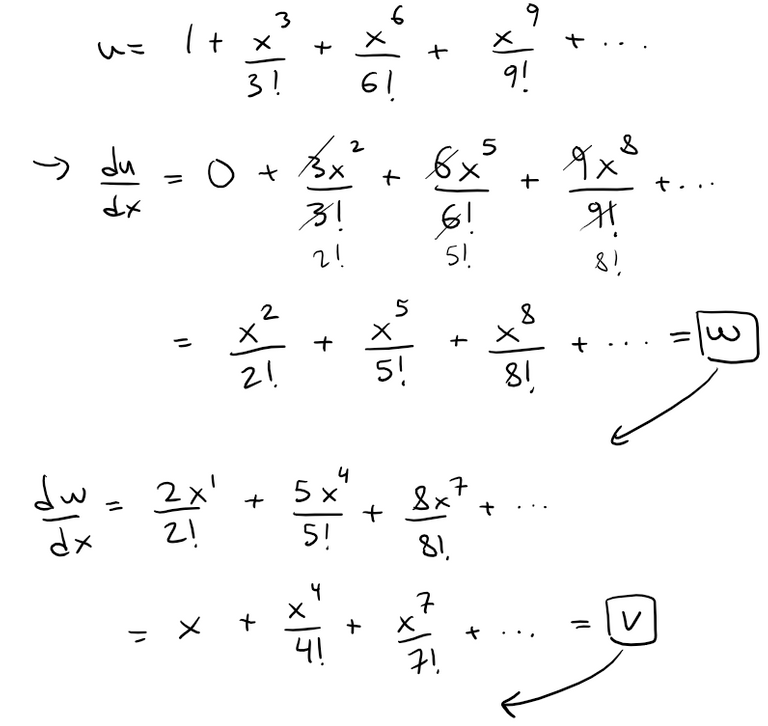

Now let's differentiate the left-hand side of the desired equation:

To find the value of the constant C, we can put x = 0 in the last equation and get:
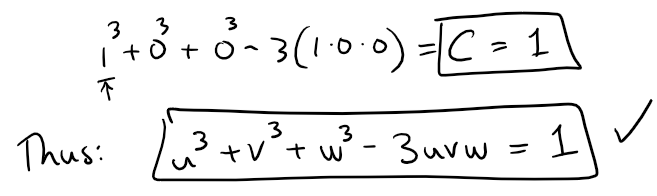
Problem 26
Prove that if n > 1, the n-th partial sum of the harmonic series is not an integer.
Hint: Let 2k be the largest power of 2 that is less than or equal to n and let M be the product of all odd integers that are less than or equal to n.
Suppose that sn = m, an integer.
Then:
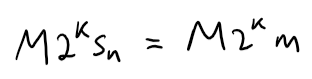
The right side of this equation is even.
Prove that the left side is odd by showing that each of its terms is an even integer, except for the last one.
Solution:
The n-th partial sum of the harmonic series (p-series with p = 1) is:
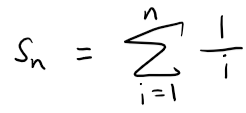
We are asked to prove that for n > 1, the partial sum is not an integer; that is, not a whole number such as -1, 0, 4, 99, etc.
Now, let's follow the hint given:
Let 2k be the largest power of 2 that is less than or equal to n.
Let M be the product of all the odd positive integers that are less than or equal to n.
Suppose that sn = m, an integer, then:
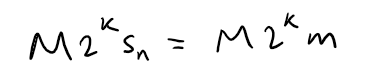
For n > 1, the right side of the above equation is an even integer.
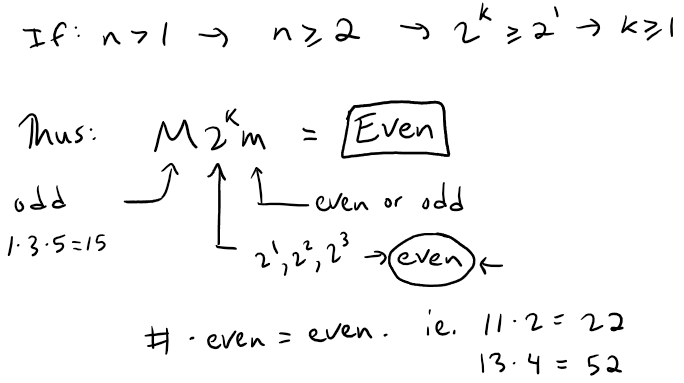
We will show that the left side of the equation is an odd integer, contradicting the equality, and thus showing that the supposition that sn is an integer must have been wrong.
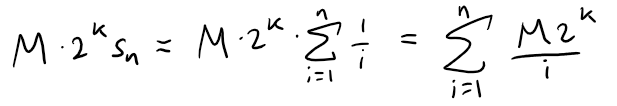
If 1 ≤ i ≤ n and i is odd, then M/i is an odd integer since i is one of the odd integers that were multiplied together to form M.
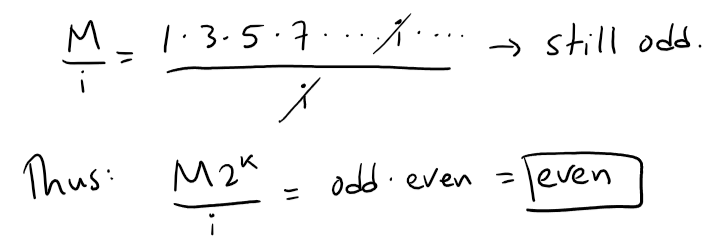
If 1 ≤ i ≤ n and i is even, then we can write i = 2rL, where 2r is the largest power dividing i, and thus L is an odd integer. This is because dividing by the largest power of 2 removes all even factors.
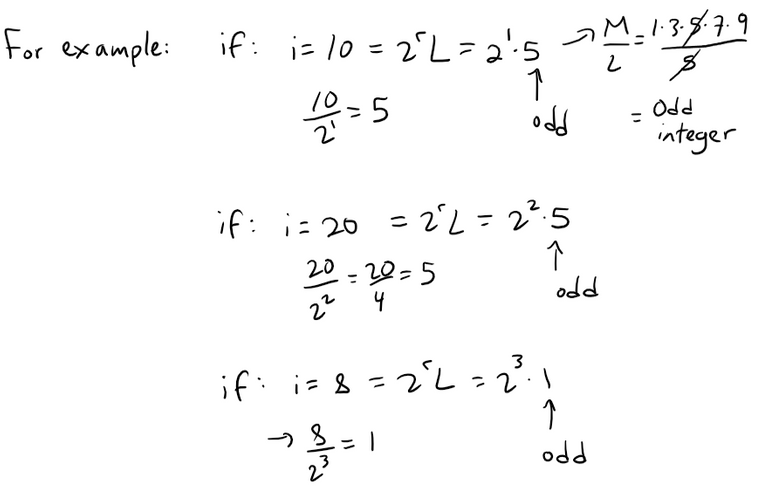
If r < k, then:
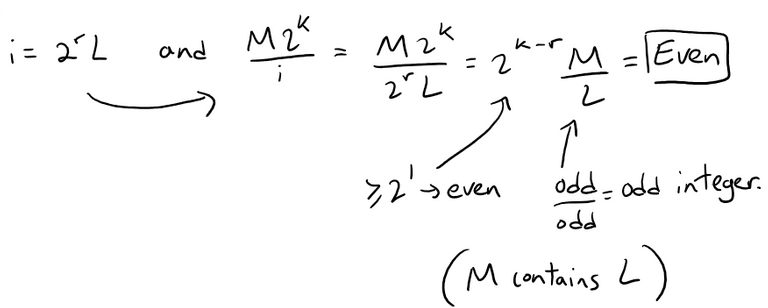
If r = k then L = 1, since:

This means that M2k/i is an even integer for every i except i = 2k and M2k/i is an odd integer when i = 2k.
This means that M2ksn is an odd integer.
This concludes the proof.
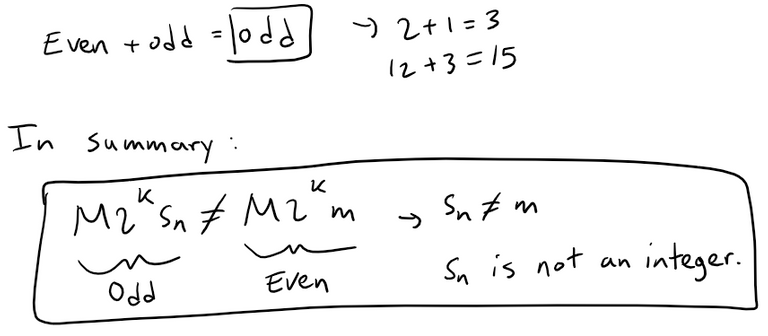
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Wow this post is so long and effect of hard work.
I noticed one mistake - Newton polynomial has radius of convergence infinity, not 1.
Thanks! I haven't covered Newton polynomials before. Where exactly did I put the R = 1 for it?
This post is so long, you could break it down into an infinite series of posts!
haha epic word play!