Fundamental Theorem of Calculus - Intro and Proof of Part 2 of the Theorem
In this video I introduce the second part of the fundamental theorem of calculus and also provide a simple proof for it. This theorem states that the integral from a to b of a function, f, is just equal to the antiderivative, F, at point b minus F at a. This greatly simplifies solving the integral which was defined in a very complex method using infinite rectangles. This is one of the most important theorems in all of mathematics so make sure you fully understand this!
Watch video on:
- 3Speak:
- BitChute: https://www.bitchute.com/video/oUdtutVlekro/
- DTube: https://d.tube/#!/v/mes/QmQXEn7JteKj1yx1rhbSB8Hz4n7gMqsSAGqVP5Fb3kCU5C
- YouTube: https://youtu.be/yuIl-BPQHss
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiYU26hyF51tkErC80g?e=0QHWcq
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Subscribe to MES Truth: https://mes.fm/truth
MES Links Telegram channel: https://t.me/meslinksJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Fundamental Theorem of Calculus - Intro and Proof of Part 2 of the Theorem
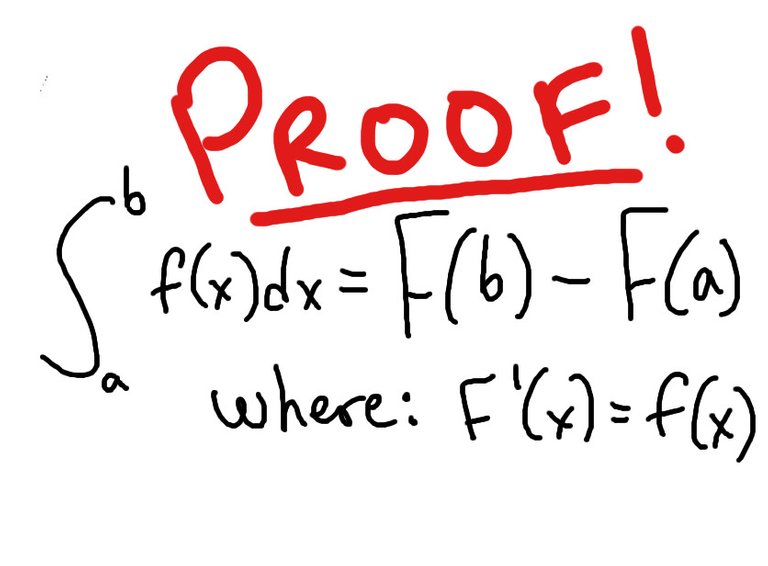
Recap on FTC 1 and FTC 2
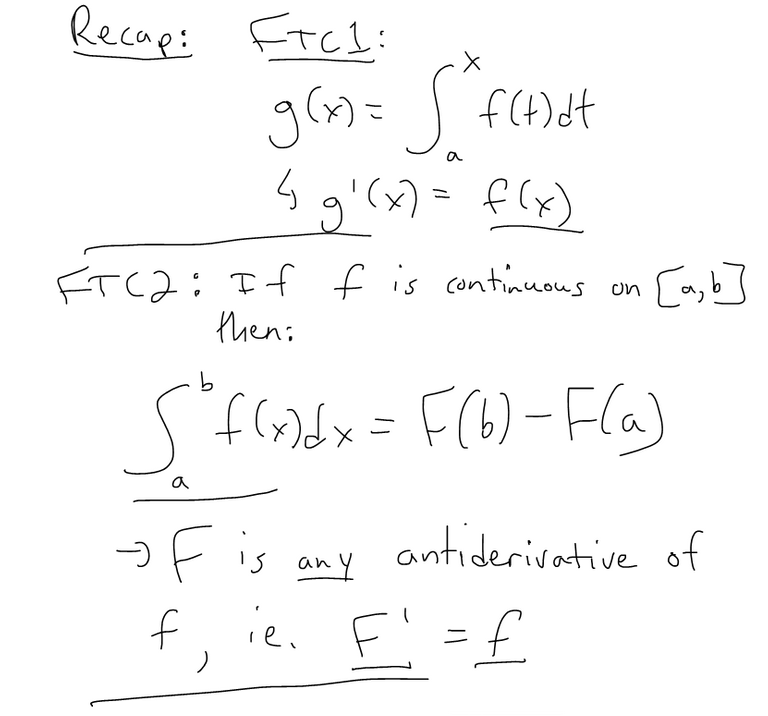
Proof FTC 2


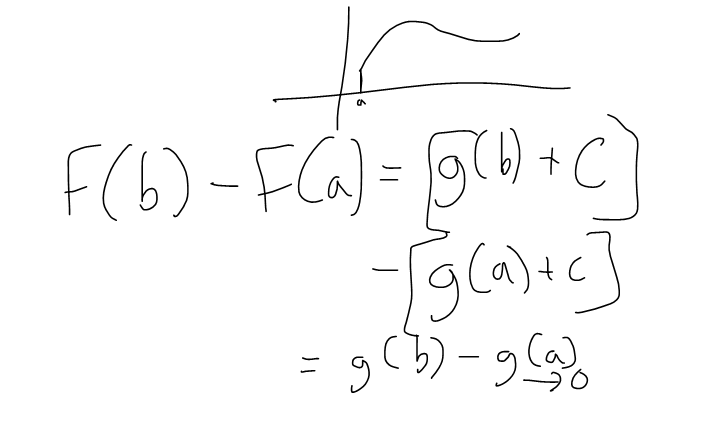
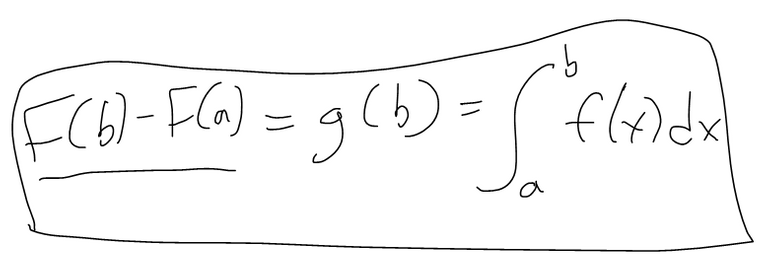
Notes
Some Notes:
- If we know the antiderivative F of f we can easily evaluate the integral by subtracting the values of F at the endpoints
- Surprising that since the integral was defined by a sum of infinite rectangles from a to b, the solution using antiderivatives is very simple.
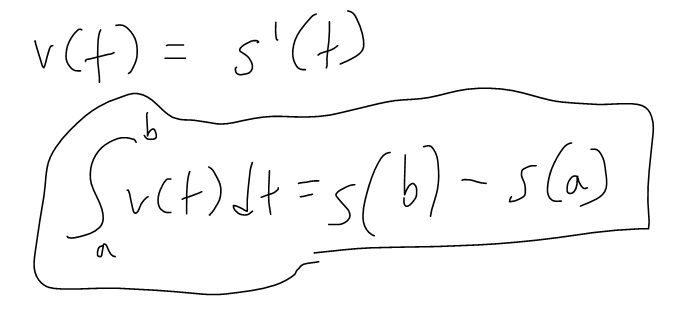
https://twitter.com/MathEasySolns/status/1509392980804734980
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
This is very educative.