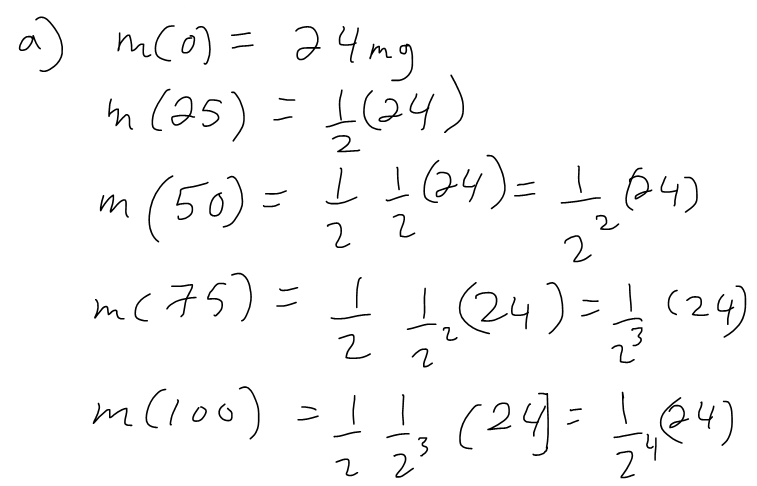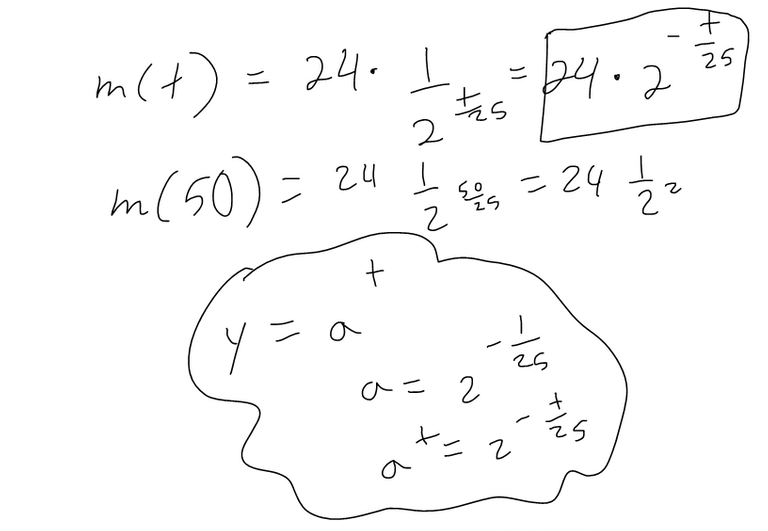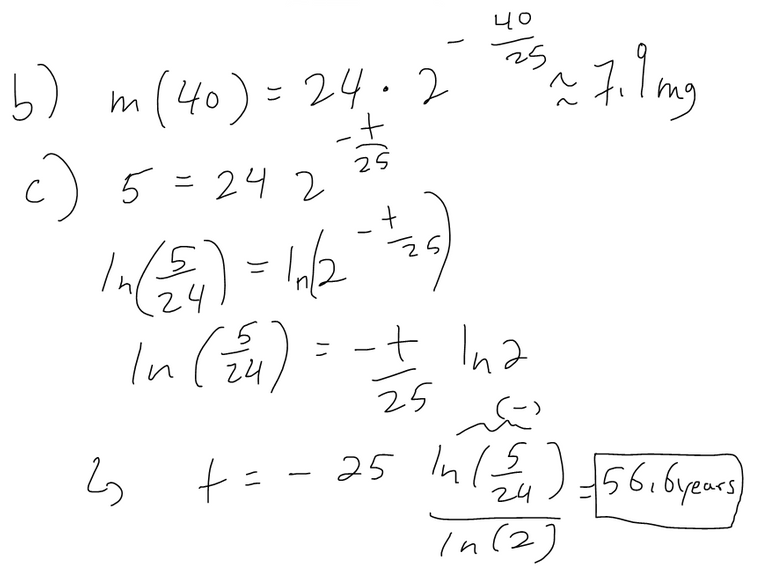Exponential Functions - Example on Radioactive Decay and Half-Life
A while ago I made a video on exponential functions but didn't get the chance to go over some very useful examples. Which is why I made this video, where I go over an example on radioactive decay and determining the exponential function of Strontium-90 decay if we are given it's half life. I also go over what half life is and show how to determine the required time to decay to a certain mass or the mass after a certain time. This concept is very important especially in dating fossils and other materials and has led to good estimates of the age of the earth. So make sure to watch this video!
Watch video on:
- BitChute:
- 3Speak:
- DTube: https://d.tube/#!/v/mes/rxfo05s03l0
- YouTube: https://youtu.be/dmMRX82zqlc
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiOEad6U4jj75a1fm_w?e=gIUoHY
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/storeReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Subscribe to MES Truth: https://mes.fm/truthJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- Browser extension recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
-- Android app: https://mes.fm/speech-android
Exponential Functions – Example on Radioactive Decay
Example
The half-life of strontium-90, 90Sr, is 25 years. This means that half of any given quantity of 90Sr will disintegrate or decay in 25 years.
(a) If a sample of 90Sr has a mass of 24 mg, find an expression for the mass m(t) that remains after t years.
(b) Find the mass remaining after 40 years.
(c) Find the time it takes for the sample to decay to 5 mg.
Solution