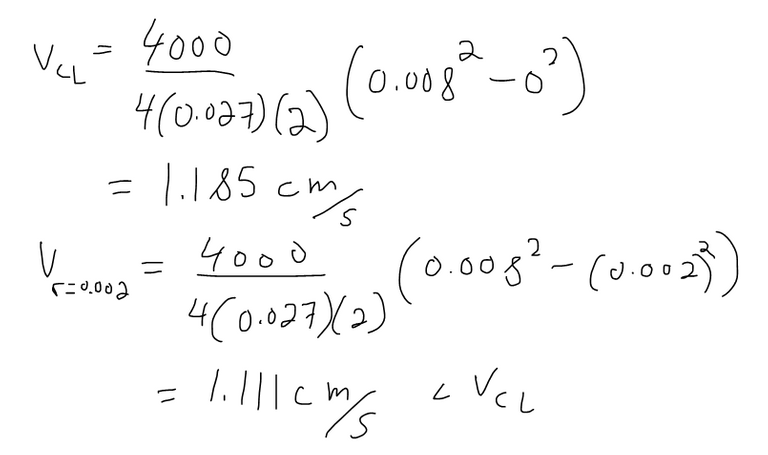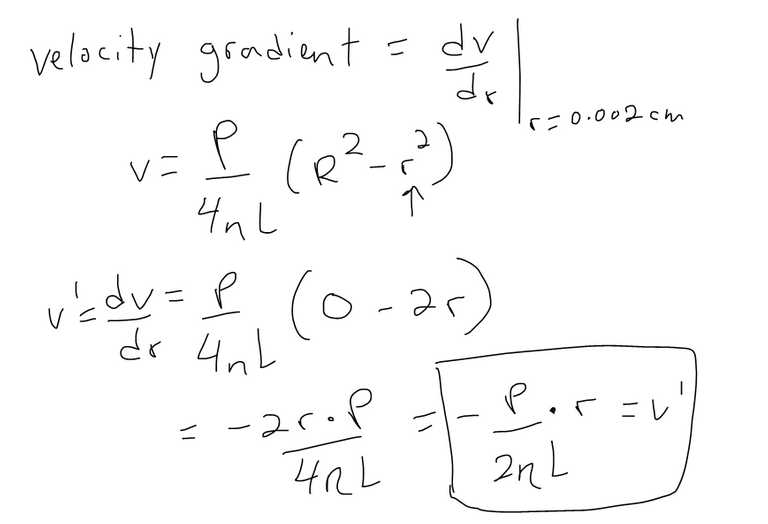Derivatives Application: Blood Flow
In this video I go over another derivatives application video and show how blood flow can be modeled by considering the rate of change of the blood velocity with distance from the center of the vein or artery as a derivative.
Watch video on:
- BitChute: https://www.bitchute.com/video/SyOR5ouRyKVa/
- 3Speak:
- DTube: https://d.tube/#!/v/mes/ugegu2t4swz
- YouTube: https://youtu.be/nTFJ57uDwtw
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiKs3LYbLL7qLIiuqFA?e=lFtHvq
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord chat room: https://mes.fm/chatroom
Check out my Reddit and Voat math forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ speed by browser extensions or modifying source code.
-- Browser extension recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this browser extension recommendation: https://mes.fm/volume-extension
Derivatives Application: Blood Flow
Blood Flow
When we consider the flow of blood through a blood vessel, such as a vein or artery, we can take the shape of the blood vessel to be a cylindrical tube with radius R and length L as illustrated below.
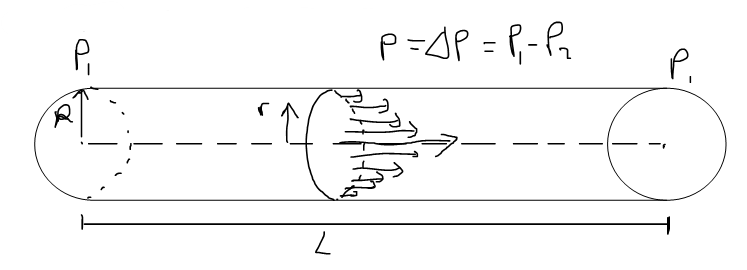
Because of friction at the walls of the tube, the velocity v of the blood is greatest along the central axis of the tube and decreases as the distance r from the axis increases until v become 0 at the wall.
The relationship between v and r is given by the law of laminar flow discovered by the French physician Jean-Louis-Marie Poiseuille in 1840. This states that:
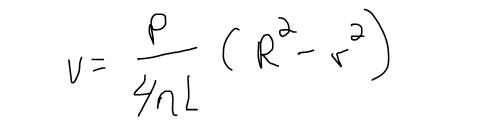
where η (Greek letter eta) is the viscosity of the blood and P is the pressure difference between the ends of the tube. If P and L are constant, then v is a function of r with domain [0,R] or 0 ≤ r ≤ R.
The average rate of change of the velocity as we move from r = r1 outward to r = r2 is given by:

If we let Δr → 0, we obtain the velocity gradient, that is, the instantaneous rate of change of velocity with respect to r:

Example
For one of the smaller human arteries we can take η = 0.027, R = 0.008 cm, L = 2 cm, and P = 4000 dynes/cm2. (1 dyne = 1 g·cm/s2 = 10-5N)
How fast is the blood flowing at the centerline and at r = 0.002 cm? What is the velocity gradient at r = 0.002 cm?