Derivative Rules - Constant Multiple, Sum, and Difference Rules

avatar
(Edited)

In this video I derive differentiation rules for taking the derivative of functions multiplied by a constant or functions added or subtracted to other functions.

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIieIbED1rpR7RdIgbOw?e=XBhGbB

Watch video on:

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truth

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

Join my forums!

Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

Browser extension recommendations:

Derivative Rules

Derivative Rules - Constant sum rules Resized AI.jfif

Constant Multiple, Sum, and Difference Rules
Constant Multiplef(x) = c·g(x)
Sumf(x) = g(x)
Differencef(x) - g(x)

Constant Multiple Rule

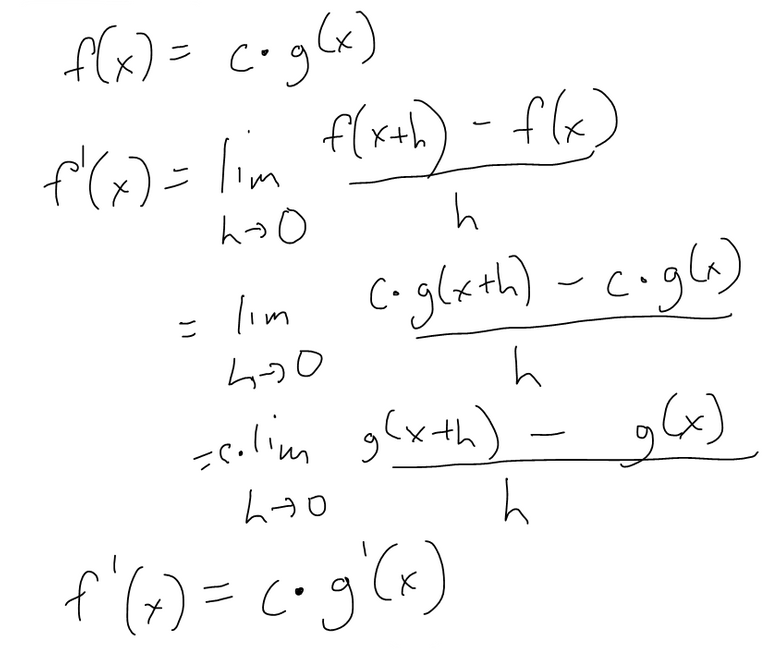
image.png

Example 1

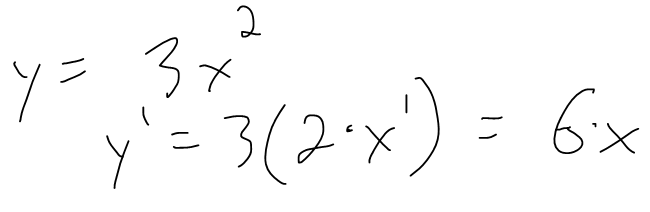
image.png

Sum and Difference Rules

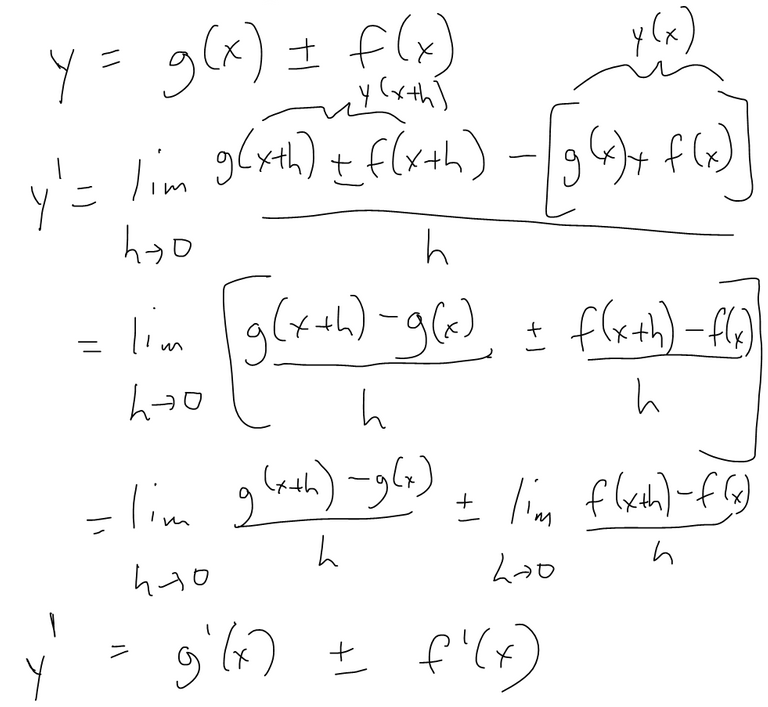
image.png

Example 2

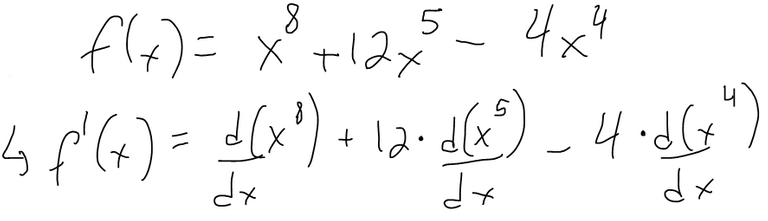
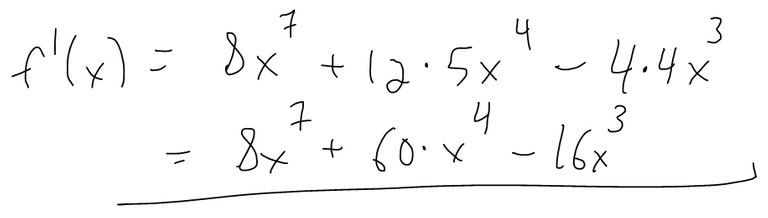
image.png

image.png

mathematics calculus science stemgeeks stemsocial palnet proofofbrain stem education math
0
0
0.000
6 comments
avatar

I need extensive calculus lessons if you ever get the chance. What textbook would you recommend? I need to start from the top.

0
0
0.000
Reply
avatar

The calculus book that I am currently following on my Channel is the Stewart Calculus Early Transcendentals 7th Edition, and I would definitely recommend that book! You can download a copy here: https://1drv.ms/b/s!As32ynv0LoaIiY10LN5fSonL4d97ow?e=YePSK5

You can also search through my older videos on Calculus: https://www.youtube.com/@mes/search?query=calculus

0
0
0.000
Reply
avatar

Thank you very much! I have an extreme workload, so I'm afraid it may not be soon but it's definitely something I want to do. I only made it in school to around grade 9. Since then, I've been in college for a few years but there are definitely huge fundamental gaps that I'm missing and can't seem to pinpoint them.

That said I've cautiously and casually admired your work. I hope to reach out to you for stuff in the near future.

0
0
0.000
Reply
avatar

Sounds good. It's never too late to learn math! Feel free to ask me any questions and wish you the best of luck!

0
0
0.000
Reply