Complex Numbers as Rotation Matrices

avatar
(Edited)

In this video I go over a very interesting concept and that is in interpreting complex or imaginary numbers as and equivalent rotational matrix form. This concept was brought to my attention by Lori Gardi from the Fractal Woman YouTube channel. Rewriting complex numbers as rotation matrices allows for looking at complex numbers from a different perspective, and this case that perspective is in simply rotating vectors. The imaginary number "i" is thus viewed as simply a 90 degree rotation when viewed as a rotation matrix. I also rewrite the famous Euler's formula into a rotation matrix form and that turns out to just be a 180 degree rotation. Since complex numbers appear often in mathematics and physics, it may be insightful to reinterpret such complex equations as simply vector rotations!

Note that while I only covered 2D rotation matrices, a similar concept can be applied to 3D rotation matrices, and which I may cover in future videos so stay tuned.

The topics covered as well as their timestamps are listed below.

  • Introduction: 0:00
  • Topics to Cover: 0:41
  1. Fractal Woman and Other References: 1:28
  2. Rotating a Vector: 3:01
  3. Matrix Multiplication: 12:47
  4. Matrix Addition: 25:29
  5. Rotation Matrix: 27:13
  6. Complex Numbers: 36:58
  7. Relating the Complex Plane with the Rotation Matrix: 43:30
    • Complex Numbers as Vector Rotations: 57:12
    • Reinterpreting Euler's Formula: 1:10:02
    • Applications to Other Fields: 1:20:51

Watch video on:

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiaFTZDoqo7BXtv_aCQ?e=vfGRLy

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truth

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

Join my forums!

Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

Browser extension recommendations:

Complex Numbers as Rotation Matrices

Complex Rotation Matrix.jpeg

Topics to Cover

The topics covered are listed below, and their timestamps will be included in the video description.

  1. Fractal Woman and Other References
  2. Rotating a Vector
  3. Matrix Multiplication
  4. Matrix Addition
  5. Rotation Matrix
  6. Complex Numbers
  7. Relating the Complex Plane with the Rotation Matrix
    • Complex Numbers as Vector Rotations
    • Reinterpreting Euler's Formula
    • Applications to Other Fields

Fractal Woman and Other References

I got the inspiration to make this video from Lori Gardi's YouTube channel called "Fractal Woman", which I have linked below.

https://www.youtube.com/user/FractalWoman/search?query=complex%20numbers
Retrieved: 15 November 2022
Archive: https://archive.ph/wip/LH2I5

image.png

Note that Lori states she got this idea from Robert Distinti of the "www.Distinti.com" YouTube channel:

https://www.youtube.com/user/rdistinti/search?query=complex%20numbers
Retrieved: 17 November 2022
Archive: https://archive.ph/wip/r0Qwl

image.png

Listed below are some sources which I used in the making of this video.

  • SymPhys video derivation:
  • Euler's formula: https://en.wikipedia.org/wiki/Euler%27s_formula
  • Rotation matrix: https://en.wikipedia.org/wiki/Rotation_matrix#Relationship_with_complex_plane
  • Vectors: https://peakd.com/hive-128780/@mes/vectors-and-the-geometry-of-space-vectors
  • Matrix multiplication: https://en.wikipedia.org/wiki/Matrix_multiplication
  • Matrix addition: https://en.wikipedia.org/wiki/Matrix_addition
  • Complex number: https://en.wikipedia.org/wiki/Complex_number
  • Imaginary unit, i: https://en.wikipedia.org/wiki/Imaginary_unit
  • Euler's formula: https://en.wikipedia.org/wiki/Euler%27s_formula

    • Rotating a Vector

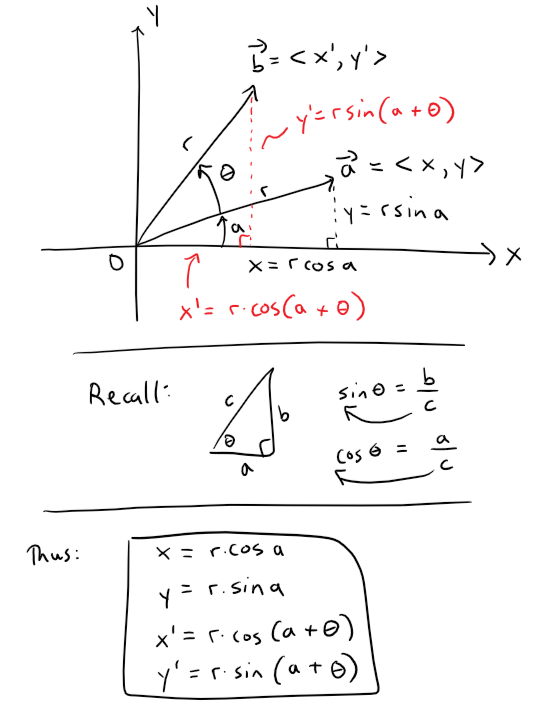
    Let's consider what happens when we rotate a vector by an angle θ:

    image.png

    Recall the following trigonometric identities from my earlier videos.

    cos(A ± B): https://youtu.be/VuQczhk7HOs
    sin(A ± B): https://youtu.be/edtk9thfwbM

    cos⁡(A ± B) = cos⁡A⋅cos⁡B ∓ sin⁡A⋅sin⁡B
    sin⁡(A ± B)= sin⁡A⋅cos⁡B ± cos⁡A⋅sin⁡B

    Thus, utilizing the addition identities we obtain:

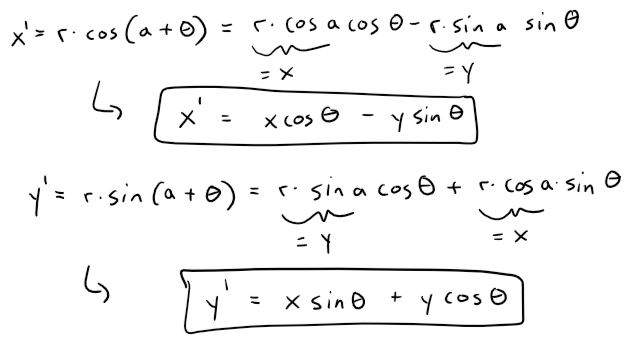
    image.png

    Matrix Multiplication

    A matrix (plural is matrices) is just a rectangular array or table of numbers, symbols, or expressions, such as the following 2x2 matrix.

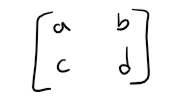
    image.png

    Multiplying 2 matrices, A and B, is defined such that it produces a second matrix C and denoted AB, and follows the rules listed below:

    • The number of columns of the first matrix A must equal to the number of rows in the second matrix B.
    • The resulting matrix has the number of rows of the first A and the number of columns of the second matrix B.

    MES Note: Typically the notation for a matrix is to bold the symbol, such as A, but I will use the following notation as well where it is more clear: [A].

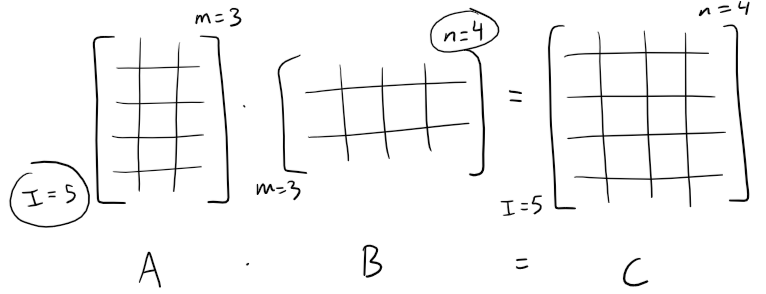
    image.png

    The values in C or AB involve multiplying each corresponding row of A with each corresponding column of B and summing them up as follows:

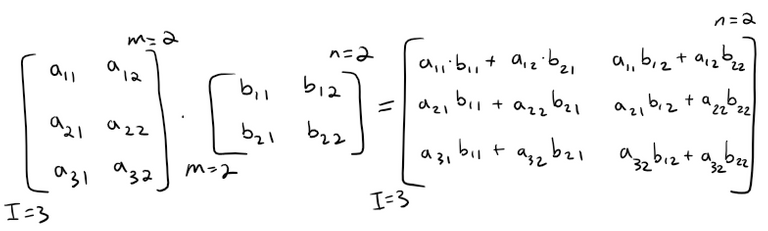
    image.png

    Matrix Addition

    Matrix addition requires that two matrices have equal number of rows and columns, and the result is that each corresponding entry simply adds up together; as the following example illustrates:

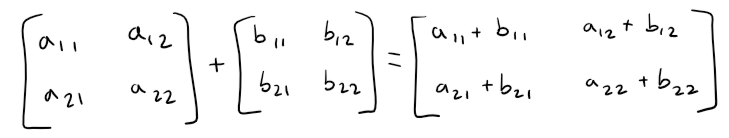
    image.png

    Rotation Matrix

    Now let's get back to our earlier vector rotation and summarize what we have:

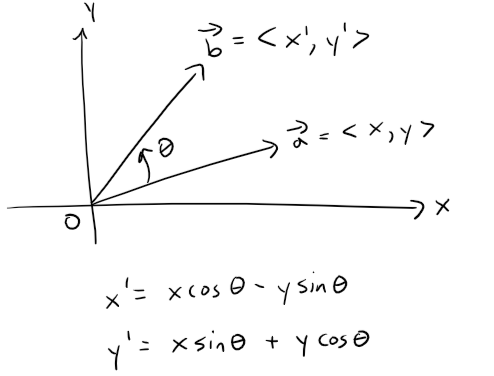
    image.png

    Let's try now to convert our vector rotation into an equivalent matrix form.

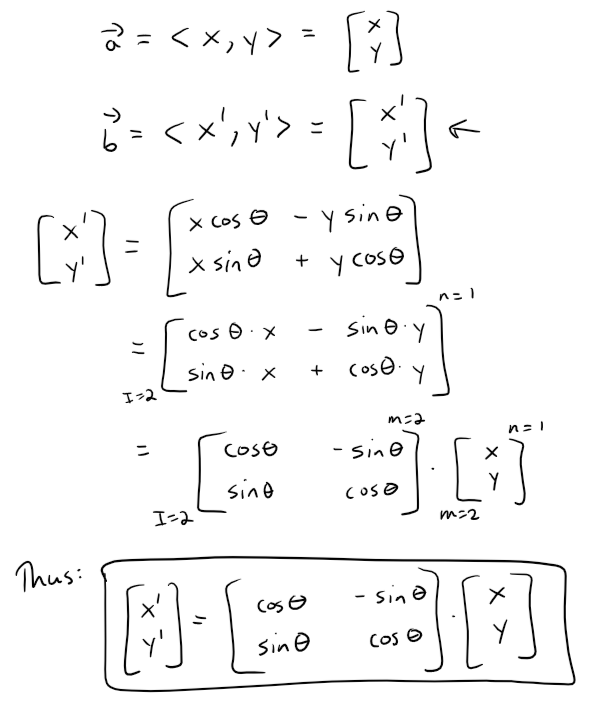
    image.png

    The above 2x2 matrix is called the Rotation Matrix, which we denote by R or R(θ), since it rotates the vector a by θ.

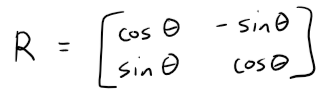
    image.png

    Complex Numbers

    I had done a video on Complex or Imaginary Numbers 11 years ago, but it is a bit outdated and unpolished as it was one of my first videos on the channel.


    Retrieved: 15 November 2022
    Archive: https://archive.ph/wip/U9bdF

    image.png

    Let's now start fresh here.

    A complex number is an extension of real numbers by using the imaginary unit, i.

    The imaginary unit, i, is a solution to the equation:

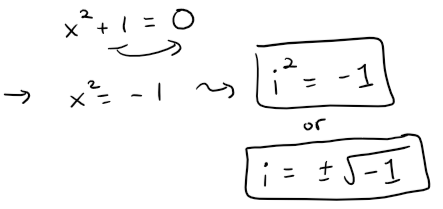
    image.png

    Because no real number satisfies the above equation, i was called an "imaginary number".

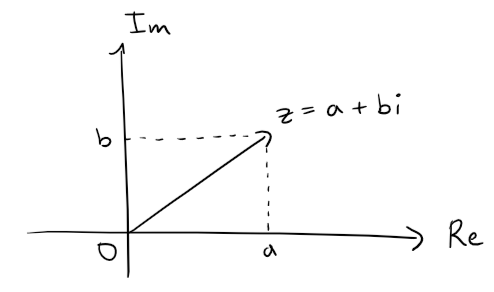
    Complex numbers are written in the form:

    z = a + bi

    where a and b are real numbers.

    The a term is considered the real part and the b term is considered the imaginary part.

    A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram; where the imaginary axis (Im) is the vertical axis and the real axis (Re) is the horizontal axis.

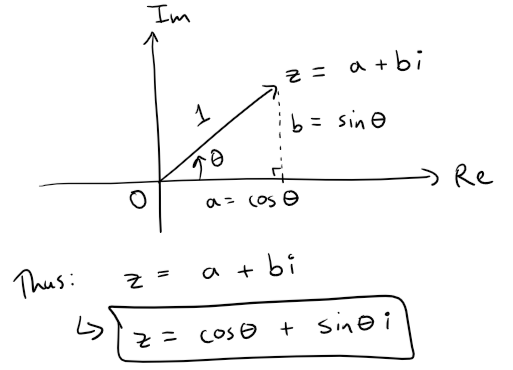
    image.png

    Let's break down the complex number z into its component parts via the angle θ and only consider the unit length of 1 since we only want to consider rotation for now.

    image.png

    Relating the Complex Plane with the Rotation Matrix

    Let's try to manipulate our previous rotation matrix equation to try to get it in a form similar to the above complex equation.

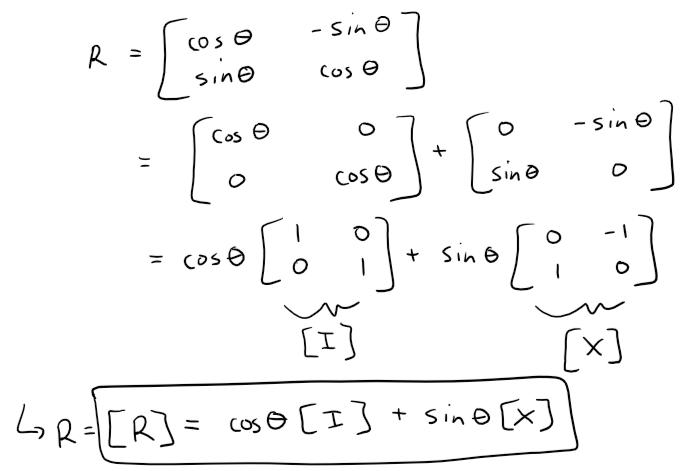
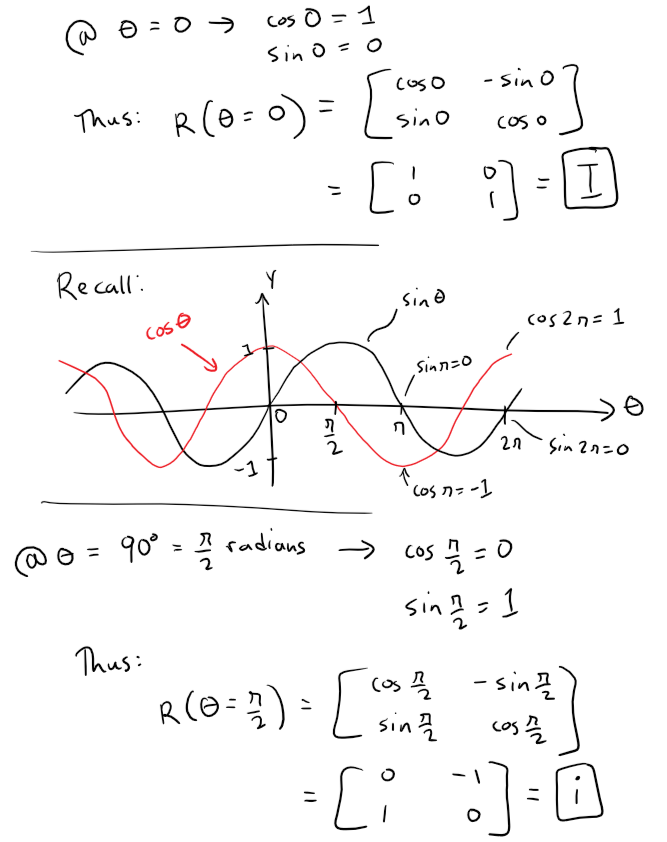
    image.png

    Note that the I matrix above is called the "Identity Matrix".

    Let's compare our above expression with that of the unit complex number equation we derived earlier.

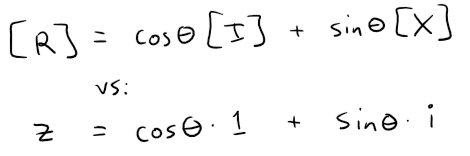
    image.png

    Now let's compare the properties of I and X with that of 1 and i.

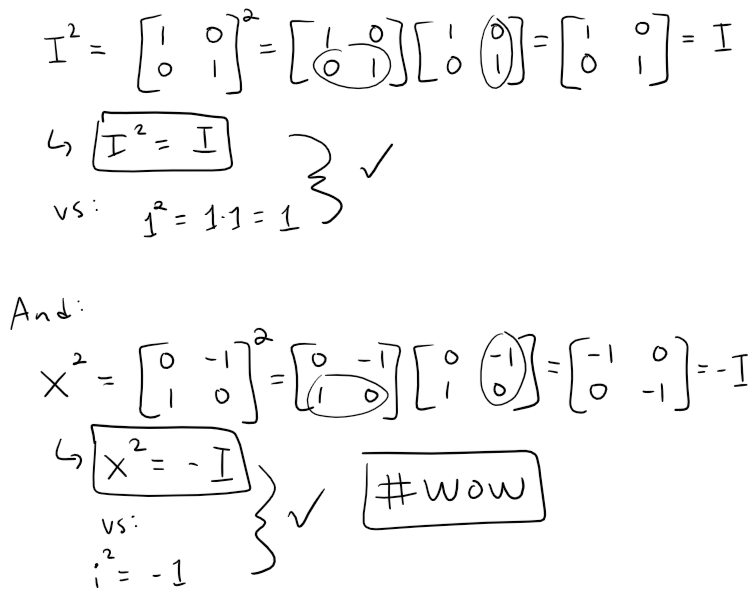
    image.png

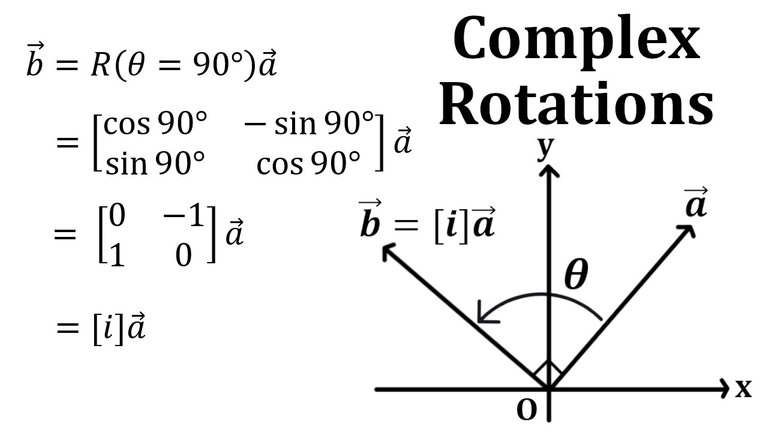
    Thus we can say that our Rotation matrix is equivalent to an unit Complex number. #Amazing

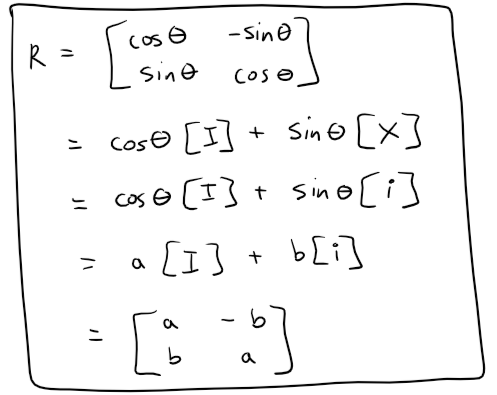
    image.png

    Complex Numbers as Rotations

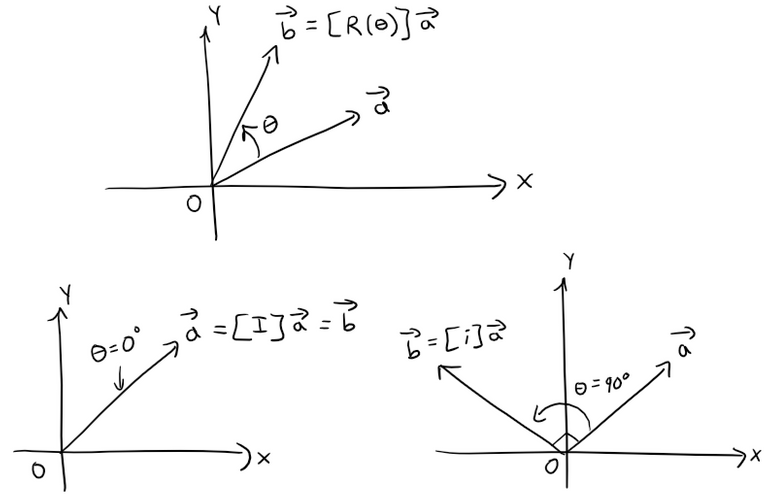
    The identity matrix I and the unit imaginary matrix i can be viewed as rotations of 0° for I and 90° for i.

    image.png

    Equating unit complex numbers to rotation matrices effectively means that we can interpret unit complex numbers as applying a rotation to another vector.

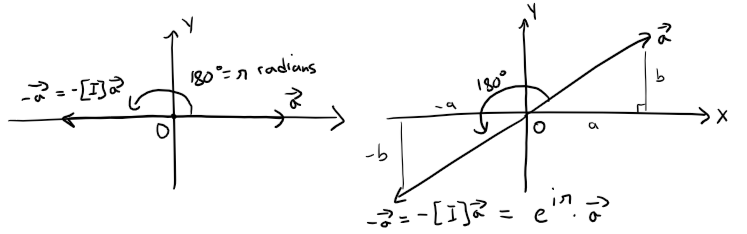
    image.png

    Note that if we rotate by a full 360 degrees or 2π radians, we get back to where we started!

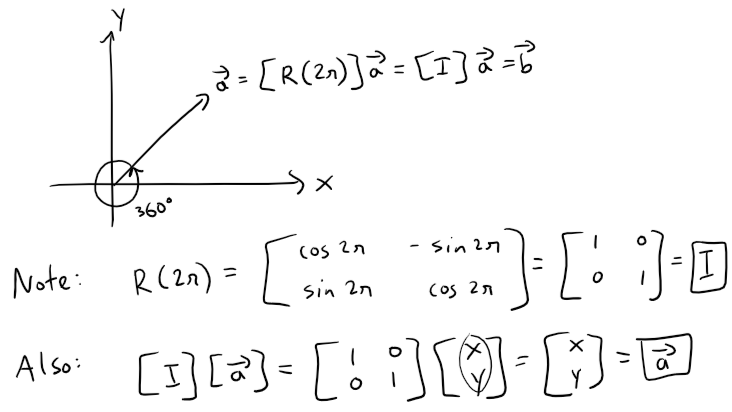
    image.png

    Reinterpreting Euler's Formula

    Let's now consider the famous Euler's formula and reinterpret it as a 2x2 rotation matrix.

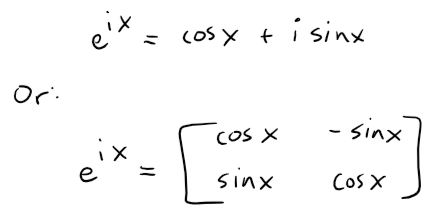
    image.png

    When x = π, we get Euler's identity:

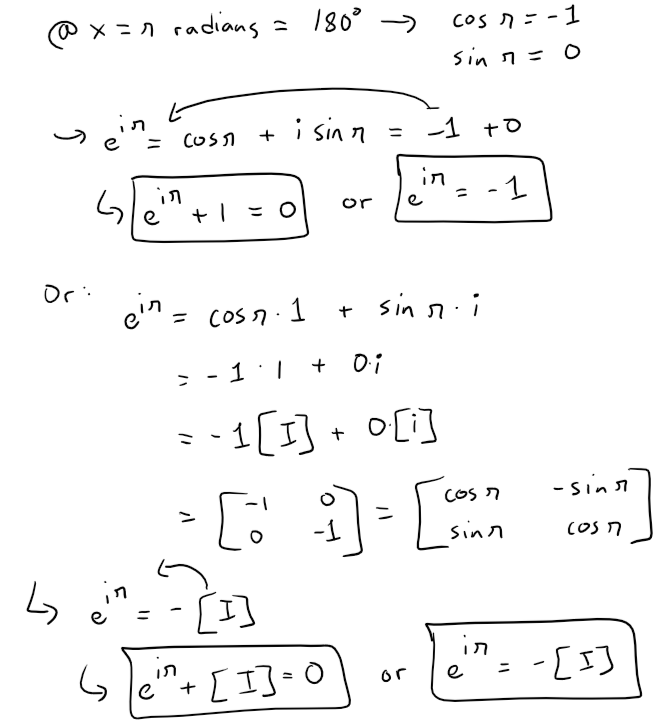
    image.png

    In other words, eiπ is just a rotation matrix that rotates a vector by 180 degrees.

    image.png

    Applications to Other Fields

    Since complex numbers are applied to many different fields in mathematics and physics, including electromagnetism and quantum mechanics, reinterpreting such equations as rotational matrices may provide unique insights!

    Try investigating yourself and let me know what you discover!

    Finally, we covered 2D rotational matrices, but the concept is similar when dealing with 3D, which is something I may cover in future videos, so stay tuned.

    mathematics calculus science stemgeeks palnet proofofbrain vectors math stem education
    0
    0
    0.000
    0 comments