Absolute Values - Properties and Rules
A while ago, I did a video introducing absolute values and what they were but I did not go through some very useful properties and rules of absolute values. In this video I go over these properties and show, for example, that sqrt(a2) = absolute value of a. I go over some other useful properties so make sure you watch the video!
Watch video on:
- 3Speak:
- BitChute: https://www.bitchute.com/video/FgjyJg4BgNHU/
- DTube: https://d.tube/#!/v/mes/7fm4839qsew
- YouTube: https://youtu.be/tl9iten87MU
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiOhTklVbOXFgxHQM-Q?e=3vNErG
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Subscribe to MES Truth: https://mes.fm/truth
Join my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Absolute Values: Properties

Recap
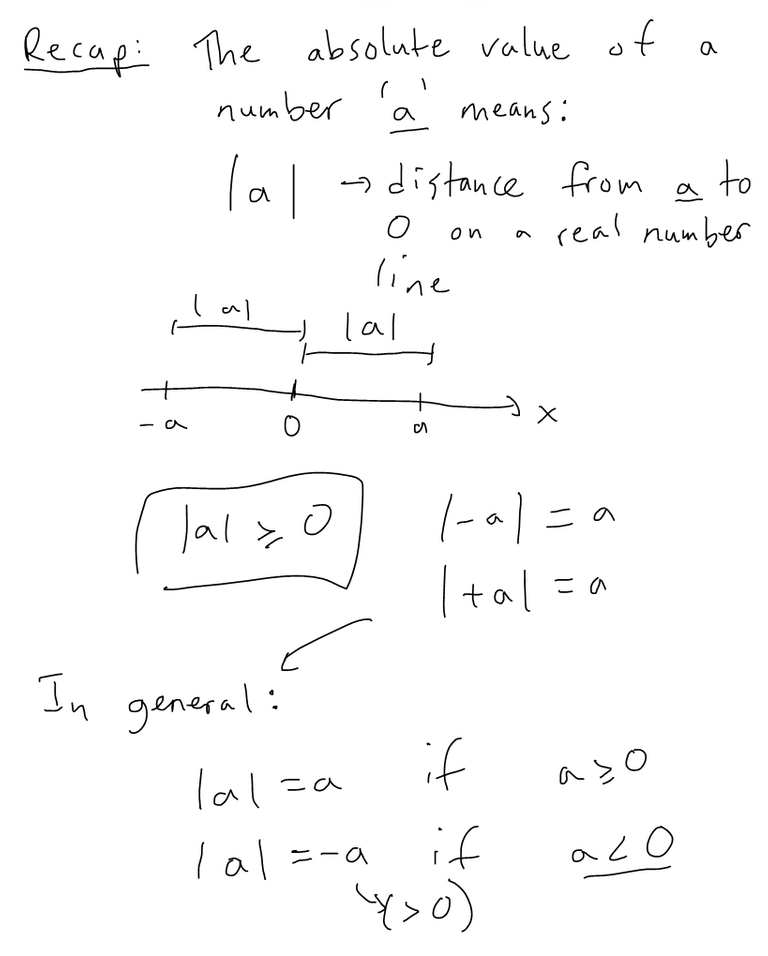
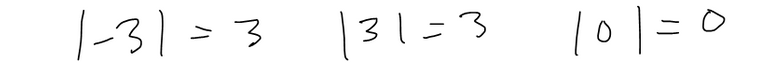
Properties
(1). √(a2) = |a|
(2). |ab| = |a||b|
(3). |a/b| = |a|/|b| where b ≠ 0
(4). |an| = |a|n
For the following rules, suppose a > 0, then:
(5). |x| = a if and only if x = ± a
(6). |x| < a if and only if – a < x < a
(7). |x| > a if and only if x > a or x < – a
Rule 1

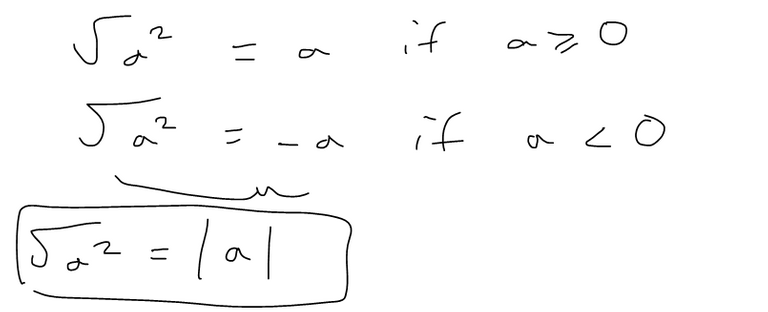
Rule 2
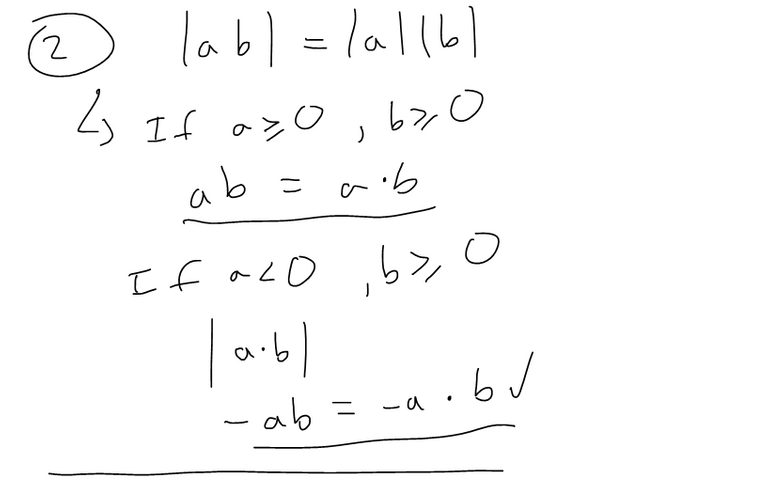
Rule 3
Same as Rule 2 because division can be changed into multiplication:
Let c = 1/b where b ≠ 0.
|a/b| = |ac| and this then follows the same procedure as Rule 2.
Rule 4
(-a)n and (+a)n can only differ in sign but have the same absolute value: ±|a|n.
Thus, |a|n just means that the result is positive, n-power doesn't affect the sign, thus it is equal to |an|.
Rules 5, 6, 7
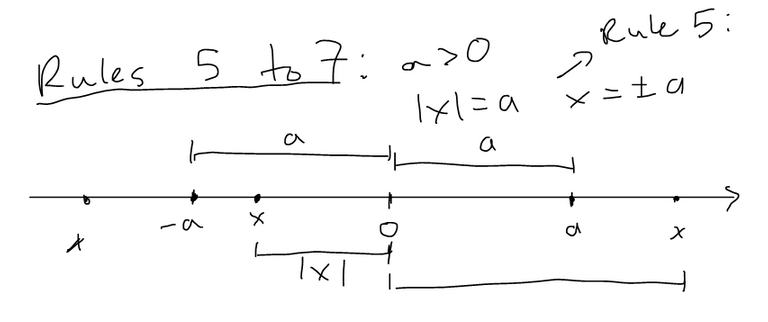
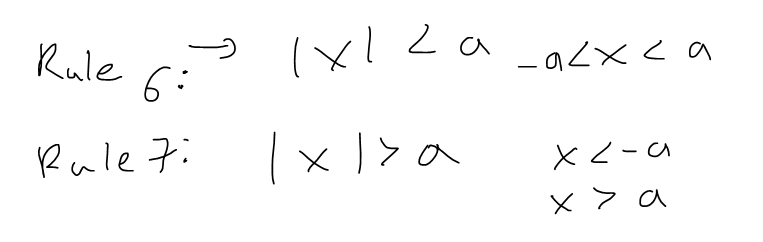
https://twitter.com/MathEasySolns/status/1419715746867736579
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
Math is not my strong point but I went ahead and watched the video. You're a great teacher and you lay it all out perfectly. The way my mind works it's kind of more right brain and imaginative. I feel things out. So as you started explaining everything and because you were explaining it so well I started daydreaming about multiple universes and fixed point in time and how they are relative 2 different supposed realities.
I kind of got lost in that thought and then I realized oh yeah I'm thinking this way because of a TV show. Sliders. This triggered all these memories from that professor and those math formulas in the first episode. Far out.
I feel confident if I watch this video a few more times while not being in the middle of doing various things I could totally grasp this no problem because you are amazing as a teacher!
I look forward to more videos!
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for Proposal
Delegate HP and earn more