Solving Linear Equations With The Distributive Law
Hello everyone. In this math post, I cover solving linear equations with the distributive law. This is suitable for early high school mathematics.

Topics
- Review Of Solving Linear Equations
- Review Of Distributive Law
- Solving Linear Equations With The Distributive Law
- Practice Problems
- Solutions To Practice Problems
Review Of Solving Linear Equations
When it comes to solving linear equations we seek to find the value of the unknown (such as x) which makes the equation hold true. For the equation x - 7 = 8, the value of the unknown x is 15.
Consider a more involved example where we have the equation 2x - 7 = 15. To find the value of x here. We add 7 to both sides to "remove" the negative seven from the left side. This leaves us with:
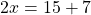
Computing the right side of 15 and 7 gives 22. We now have 2x = 22. To find the value of just x itself, divide by 2 on both sides. The value of the unknown x is just 11.
Review Of The Distributive Law
The distributive law from algebra allows for multiplication of a single term monomial with a polynomial. One example would be 5(x + 3). Multiplying the 5 through each term in (x + 3) with the distributive law yields 5x + 15.
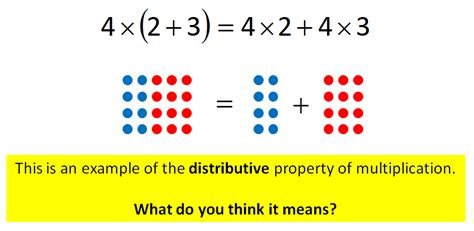
The above example dealt with a monomial with a binomial. What if the binomial was something else that was longer. Let's take a look at another example.
Using the distributive law on 8(x + 2y + z) gives 8x + 16y + 8z. The distributive law idea still holds. It is just there are more computations involved.
Solving Linear Equations With The Distributive Law
There are times when you need to certain linear equations that require the distributive law. Once you have a good grasp on using the distributive law you can easily solve for unknowns. Let's look at a few examples.
Example One
Solve for x in the equation 9(x + 2) = 22.
As soon as you see something like a number multiplied by a binomial in brackets, think of the distributive law first. (You could divide by 9 both sides and subtract by 2 to solve as an alternate approach.)
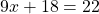
Isolate for 9x by subtracting 18 on both sides.
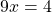
Since we want to solve for a single x divide both sides of the equation by 9. The answer for x is four ninths.
Example Two
This second example is a bit more involved. Solve for x in the equation 3(x - 7) = 5 + 8(x + 3).
Use distributive law on both sides accordingly. The equation then becomes:

Add the 2 and 24 from the right side.

Collect the x terms in one side and the numbers to the other side.

Simplify the like terms.
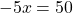
To solve for x, divide both sides by negative 5.
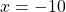
Practice Problems
In each question solve for the value of x.
3(x - 2) = 12
-5(x - 1) = 2
10x - 2 = 3(x - 4)
7(x - 2) = 9(2x + 1)
2(x + y) = 3(x - y)
Solutions To Practice Problems
6
3/5
-10/7
-23/11
5y
