Domain & Range Of Functions
Hi there. This math post is about domain and range of functions. This topic is seen in high school pre-calculus and calculus courses. It is also seen in introductory calculus courses in universities.
Math text rendered with the use of LaTeX (lay-tech) and QuickLaTeX.com.

Topics
- Quick Review Of Independent & Dependent Variables
- What Is Domain?
- What Is Range?
- Domain and Range Of Various Functions Examples
Quick Review Of Independent & Dependent Variables
An independent variable is an unknown quantity that does not depend on another variable for its amount. One common example of an independent variable is time denoted by t. In most cases, the independent variable is denoted by the letter x.
A dependent variable is a variable whose value depends on the independent variable. It is common to see the letter y for representing a dependent variable. An example of a dependent variable is a worker's take home pay as it is dependent on the number of hours worked.

What Is Domain?
In a mathematical function, the domain of a function is the set (collection) of all permissable values for the independent variable. You can also view the domain of a function as a collection of valid inputs for the function.
Given a function f(x), the domain of f(x) is the set of all possible x values for the function.
Example One
For a simple linear function such as g(x) = x + 1, the domain is any x-value (x belong to the real numbers). There is no restriction for the values of x that can be inputted into the function.
Example Two - Quadratic Function
With a quadratic function such as  , the domain is also any x-value (x belong to the real numbers).
, the domain is also any x-value (x belong to the real numbers).
Example Three - Square Root
This example features a function that has a domain that is not all real numbers for the independent variable.
It is known that it is not possible to take the square root of a negative number (in the real numbers). For the function  , the domain is
, the domain is 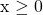 . Values for x can be 0 or greater (non-negative).
. Values for x can be 0 or greater (non-negative).
Different types of functions will have their own domain and ranges.

What Is Range?
A function's range refers to the possible outputs of a function given its function domain. The range is associated with the dependent variable of a function.
Example One
Let's revisit the linear function g(x) = x + 1. The range for this function is g(x) belongs to all real numbers  . The dependent variable can take on any value given a value from x.
. The dependent variable can take on any value given a value from x.
Example Two
With a quadratic function, you have to look for whether the parabola opens up or down from the sign in front of the x-squared term.
Given the 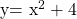 function the parabola opens upwards and its minimum is at point (0, 4). The range for this parabola function is
function the parabola opens upwards and its minimum is at point (0, 4). The range for this parabola function is  and y belongs to the real numbers.
and y belongs to the real numbers.
If given a different parabola function, you may need to use other techniques such as factoring quadratics or completing the square in order to determine the parabola vertex and intercepts.
Example Three - Rational Function
The rational function is of the form:
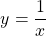
where the domain has a restriction of  .
.
The range for the rational function is  and y belongs to the real numbers. There is no x-value that can make y equal to 0.
and y belongs to the real numbers. There is no x-value that can make y equal to 0.

Domain and Range Of Various Functions Examples
Example One
The downwards facing parabola 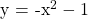 has a vertex that is a maximum at (0, -1). The domain for this function is x belongs to all real numbers. Since the vertex is a maximum, the range for this parabola is y is less than or equal to -1 with y belonging to the real numbers (
has a vertex that is a maximum at (0, -1). The domain for this function is x belongs to all real numbers. Since the vertex is a maximum, the range for this parabola is y is less than or equal to -1 with y belonging to the real numbers ( ).
).
Example Two
The trigonometric function  has a no restrictions on its domain. Any numeric value or angle can be used for its input. With the sine function, the value of sine is between -1 and +1 inclusive. The domain for the sine function is
has a no restrictions on its domain. Any numeric value or angle can be used for its input. With the sine function, the value of sine is between -1 and +1 inclusive. The domain for the sine function is 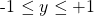 with
with  .
.
Example Three
Consider the simple exponential function 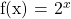 . There is no restriction on its domain so it is
. There is no restriction on its domain so it is 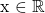 . For the range, it is important to note the exponential function has no x-intercept as there is no exponent that makes two to the power of x equal to zero. The exponential function is greater than 0 and has no upper limit. The range here would be f(x) > 0.
. For the range, it is important to note the exponential function has no x-intercept as there is no exponent that makes two to the power of x equal to zero. The exponential function is greater than 0 and has no upper limit. The range here would be f(x) > 0.
Example Four
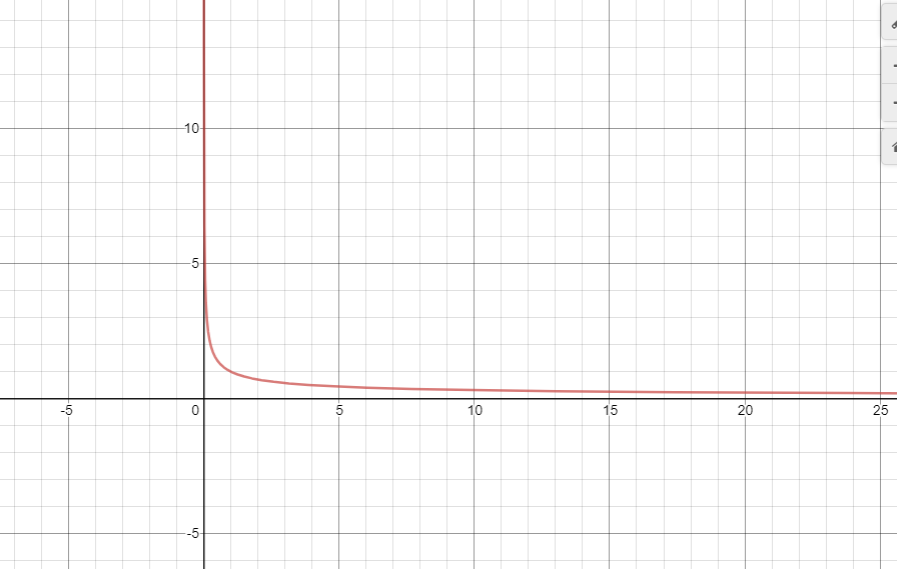
What if you have a function that is a combination of different function types? This example deals with a mixture of a reciprocal function and a square root function.
What is the domain and range for  .
.
Let's look at the square root function and the reciprocal function separately.
With the square root function, x has to be at least 0 and the square root is a number that is at least zero in its range.
With the reciprocal function  , the domain is
, the domain is  and the range is
and the range is  .
.
For  , the domain is what is common between the square root function domain and the reciprocal function domain. The domain for g(x) is x > 0. With the range, it is g(x) > 0.
, the domain is what is common between the square root function domain and the reciprocal function domain. The domain for g(x) is x > 0. With the range, it is g(x) > 0.
The plot of this function looks like this.