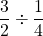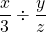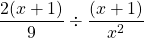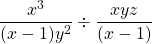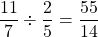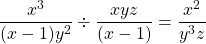Dividing Fractions
Dividing Fractions
Hi there. This math education post is on dividing fractions. Dividing fractions is a natural extension of multiplying fractions. It is assumed that the reader/student is comfortable with multiplying fractions. Harder cases of this topic include simplifying expressions with exponents and factoring.
QuickLaTeX.com is used for math text.
Topics
- Review Of Multiplying Fractions
- Just "Flip" The Second Fraction In Dividing Fractions
- Working With Variables
- Factored Form Cases
- Practice Problems
- Solutions To Practice Problems
Review Of Multiplying Fractions
Two fractions can be multiplied together by multiplying the numerators together and the denominators together to obtain a single fraction.
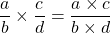
Example
Multiplying one third with 2 fifths gives 2 over 15.
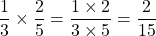
Just "Flip" The Second Fraction In Dividing Fractions
Dividing fractions just adds one more rule on top of multiplying fractions. Simply flip or take the reciprocal of the second fraction after the division sign.
Example
Divide one half by one quarter.
A more conceptual way of looking at this would be how many quarters are there in one half? The answer is two after working out the algebra.
General Case
I thought I would the general case after a simple example for division.
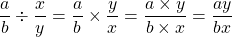
Working With Variables
When it comes to working beyond numbers we have variables. Variables are unknown values/numbers that are then known once information is given. Dividing fractions still operates the same way. It is just you deal with more symbols and letters than numbers.
Example One
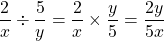
Example Two
The two over four is reduced to 1 over 2. Do simplify and reduce fractions where possible.
Factored Form Cases
In high school mathematics (around grade 10), the algebra technique of factoring is used for solving quadratic equations, higher order polynomials (with Factor Theorem). Factoring can also be used for simplifying expressions which contain fractions.
Do remember to use exponent laws when simplifying fractional expressions too!
Example
Simplify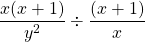 
.
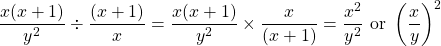
Practice Problems
In each question, divide the following fractions.
Solutions To Practice Problems
