Reasoning In Mathematics
Hi there. In this math & education post, I would like to talk about the importance of reasoning in mathematics. I do think that a lot of (early) math education focuses too much on numbers, computations, number drills and the like. There should be more emphasis in explaining answers on top of answering questions.

Being Able To Explain Answers
Explaining answers is not just limited to mathematics. In a lot of subjects, it is important to explain answers, ideas and viewpoints verbally and in writing. In mathematics education, I think that there is a large emphasis in problem solving, algebra and number computations. There may be a few good teachers out there that try to have students explain math concepts verbally through presentations or in writing through assignments and short answer questions.
As an extension those who are good in explaining technical concepts verbally and in writing to less technical audiences could thrive in fields such as teaching, consulting, coaching and even in the legal field.

Examples Of Math Reasoning
Why Is A Rectangle Not A Square?
This question is a common question for young math students when it comes to learning basic geometry. Both shapes has four right angles and opposite parallel sides. The rectangle cannot be a square as all four sides of the rectangle are not the same. All the sides of the square are of the same length.
Order Of Operations Case
Bob has an order of operations (BEDMAS) algebra expression to simplify
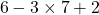
Bob obtains an answer of 16. Is Bob correct? Explain your answer.
Bob's answer is incorrect. The answer here is not 16. From order of operations the first step is multiplication before subtraction and addition. This first step would be 3 x 7 = 21 which would yield
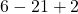
The next steps now is six minus 21 plus 2 which would be negative 15 plus 2. The actual answer is negative 13.

Extension - Math Proofs
At the higher levels of mathematics (university), mathematics is more theoretical. It is more about ideas, structures, systems, applications along with philosophy. Every math major at university/college will have some sort of exposure to math proofs through an introductory course of real analysis. After that course, students can choose if they want more theoretical math in the form of pure mathematics or choose mathematics branches that have more real world applications.
Reasoning in math proofs is much more detailed and precise. Definitions are much more technical and it is difficult for many to clearly communicate their written work. Sometimes a single sentence in a proof may require multiple rereads and thinking to fully understand it.

Which country, in your opinion, has their early math education closest to your ideal?
!discovery 31
I am not sure.
I have to first figure out what is my ideal. Plus I have to look into various countries with their math education.
For country candidates I think these countries are rigorous in their math education (before university):
There are others too (not listed).
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Dear @dkmathstats, we need your help!
The Hivebuzz proposal already got important support from the community. However, it lost its funding a few days ago and only needs support to get funded again.
May we ask you to support it so our team can continue its work?
You can do it on Peakd, Ecency, Hive.blog or using HiveSigner.
https://peakd.com/me/proposals/199
All votes are helpful and yours will be much appreciated.
Thank you!
@tipu curate
Upvoted 👌 (Mana: 0/46) Liquid rewards.
I am afraid that reasoning and logic is what seem to be what is missing most at the moment, at least with the new generation of students (in France). This is true for physics, math, and obviously for other fields too. This is what I found, when averaging (exceptions exist).
For now, I don't know whether this is a trend of this time, or a side effect of COVID on educational methods. Indicators are however all pointing in the wrong direction.
Cheers, and thanks for the interesting blog!
Felicidades su publicación ha Sido elegida entre las mejores del día.
SIGA CREANDO BUEN CONTENIDO.
So far I know you’re blessed with a creative mind and this profession best suits you, for me? Maths is not my thing