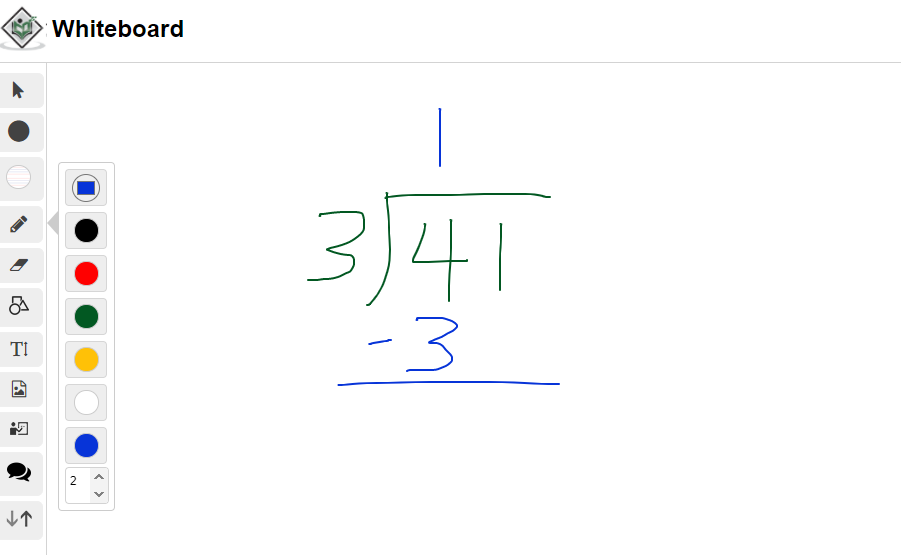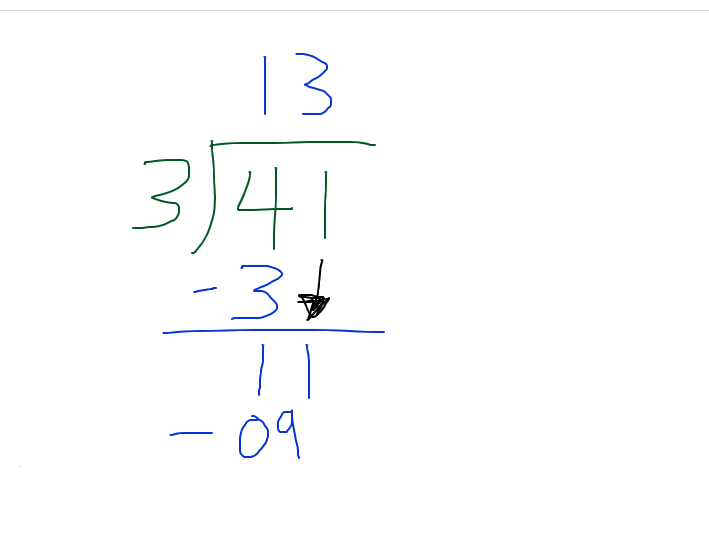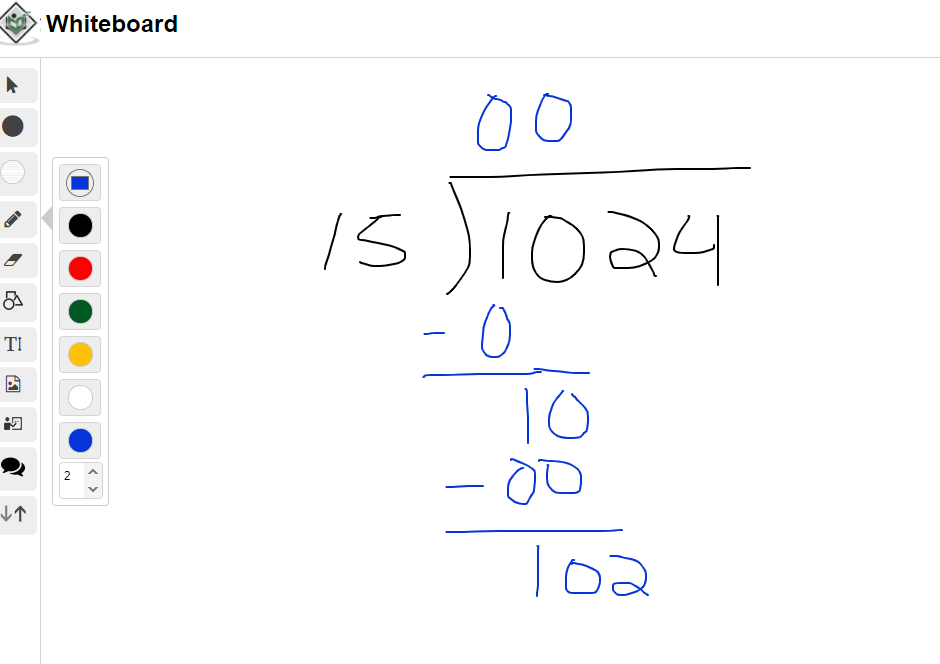A Long Division Guide
Hi there. In this mathematics education post, I cover the concept of long division. This is one of the harder topics for elementary math students as good multiplication skills are required and there are a lot of steps involved.
The Meaning Of Division
Division is the reverse of multiplication. Multiplication commonly refers to how many items in groups where each group has the same number of items. Five dozen of eggs is 5 x 12 = 60. With division, you want to find out how many groups are there from a number of items. Each group has the same number of items. As an example, from 100 cookies you can make 20 groups of 5. This would be 100 ÷ 5 = 20.
Do keep in mind that with division you may not have every item in a group. This is where the concept of a remainder comes in. Having 22 divided by 10 gives two groups of 10 with 2 left over that is not in a group. This is 22 ÷ 10 = 2R2 as 2 x 10 = 20 with 2 left over.
Long Division Examples
Doing division with two digit numbers divided by single digit numbers is not too difficult. Working with larger numbers is not easy to do mentally. If you are able to do it that is a bonus for you. Many of use would require the technique of long division, with scrap paper and pencils to do division of larger numbers.
The concept of long division here is shown through examples. I use Tutorials Point's whiteboard feature for these screenshots.
Example One
What is 41 divided by 3?
The expression 41 ÷ 3 can be expressed in the long division visual format. Remember that it is inside divided by outside. The 41 which is the dividend is on the inside and the divisor of 3 is on the left side. The answer from division is called the quotient. Quotients are on the top of the division line.
For this step, ask yourself how many threes are there in four? Or three times something gives a number without going over 4. The answer here is 1. This one is placed above the four over the line. One times the outside three gives three. This three is placed underneath the 4.
Perform the subtraction step where 4 minus 3 is 1. Bring the one from 41 down beside the first one to obtain 11.
Ask yourself now how many threes are there in eleven? The answer here is 3 as 3 x 3 = 9. Four would not work as 4 x 3 = 12 and twelve is greater than 11. Three times the outside three is 9. This nine is placed below the eleven.
Perform the subtraction step to obtain 2. As there are no more numbers to bring down this number of 2 is the remainder. The answer to 41 ÷ 3 is 13 R 2.
Example Two
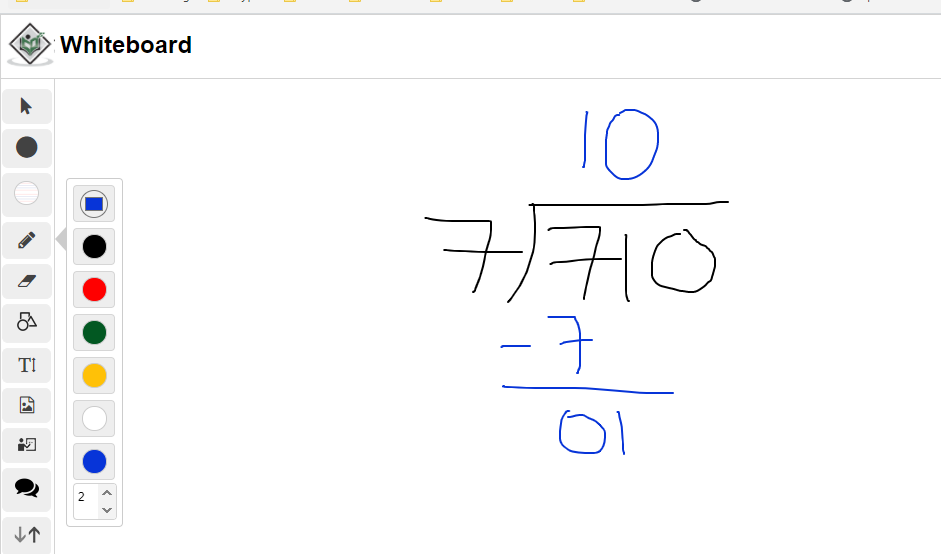
What is 710 divided by 7?
This example deals with a larger number as the dividend. The steps are similar to the one in example one. As the first step, there is one seven in seven.
For this part, there are no sevens in 1. The digit beside the one on the top is a zero.
Bringing the zero from 710 gives a 10. There is one seven in 10. The remainder is a 3. 710 ÷ 7 = 101 R3
Example Three
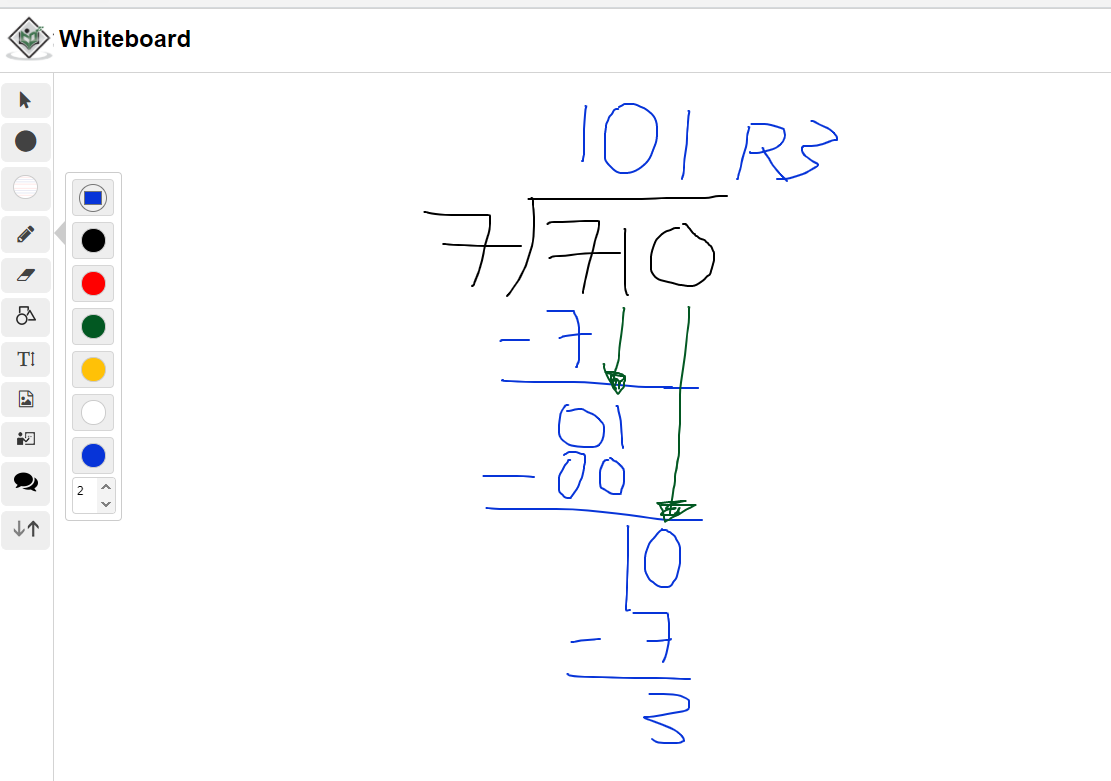
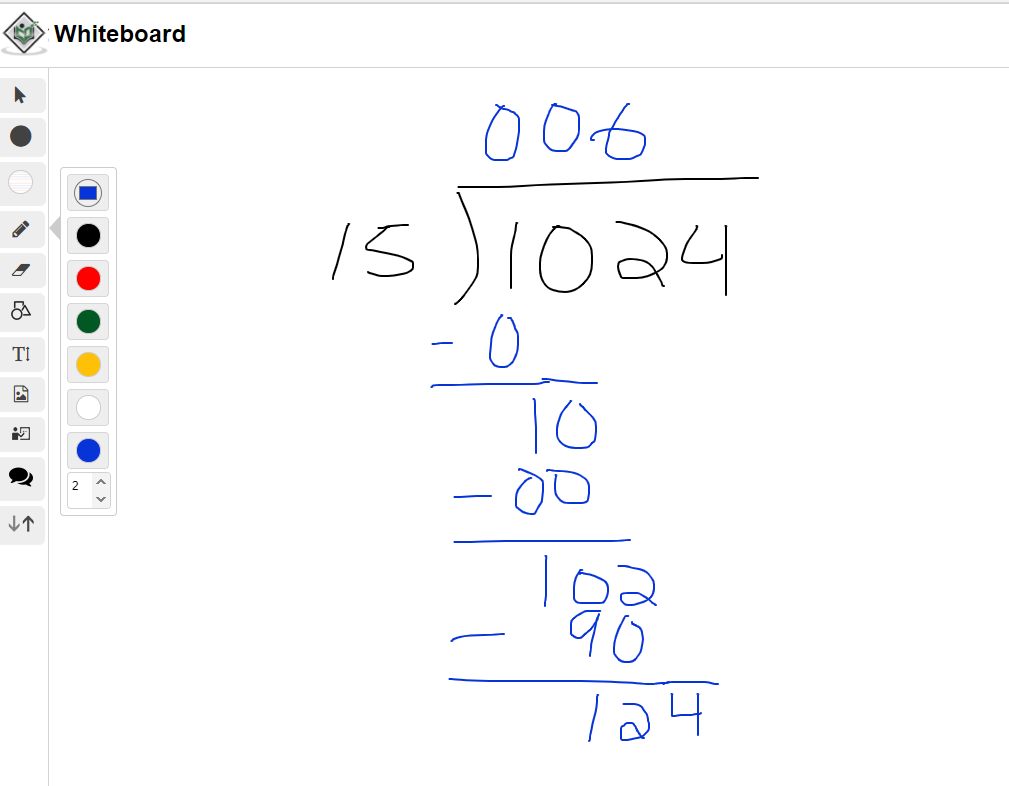
What is 1024 divided by 15?
This example has a two digit divisor of 15. It is a little bit more trickier with larger numbers but the long division steps hold. To start, there are no 15 fifteens in 1.
There is also no fifteens in 10. Another zero is placed on the top.
In this part ask yourself how many fifteens are there in 102. The answer here is 6 as 15 x 6 = 90 and 15 x 7 = 105. Write the 90 below 102 and perform the subtraction to obtain 12.
Brining the 4 down turns 12 into 124. There are 8 fifteens in 124 as 15 x 8 = 120. The remainder here is 4.
Expressing The Remainder As A Fraction
Something that I think is not really mentioned is that the remainder can be expressed as a fraction. For something such as 42 ÷ 5 the answer is 8R2 where the R2 is for a remainder of 2. This remainder of 2 can be expressed as two fifths as the remainder is 2 and we are dividing by 5.
You can also relate division with improper fractions and mixed numbers. With 42 ÷ 5 you can express this as an improper fraction and as a mixed number. (Quicklatex.com is used)

Example One
Having 132 divided by 10 gives 13 remainder 2. This is also 13 and two tenths or 13 and one fifth.
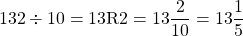
Example Two
Doing 77 divided by 2 gives 38 with a remainder of 1.
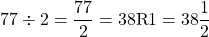

Extension - Polynomial Division
Many people see long division with numbers. The topic of polynomial division is not seen as much as there is a bit of algebra involved. It is also more for high school math students. Polynomial division uses a polynomial of something like 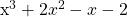 and divides it by a lower order polynomial such as
and divides it by a lower order polynomial such as x - 1. The answer would be 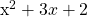 .
.
Note that the screenshot below does not show all the steps involved. I use the Math is Fun Drawing part of the website.