How often do you want to succeed?
Hi Everyone,

What is success? How do we define what success is? I think we all have our versions of what it means to be successful. Success is a very important part of our lives. I believe we all strive for some form of meaningful success. This could be in our work; in our personal life; in sports, games and competitions; in our finances; and even in our philosophy. We most likely want to be successful in many areas. Success can affect our quality of life both financially and non-financially. Hence, success should be an area discussed in economics.
I do not believe a universal definition of success is possible. I believe success is whatever you want it to be. I do not believe there is a common yardstick. I believe we can set the yardstick ourselves. If we are not able to set that yardstick, then maybe other people have too much influence over our lives.
The yardstick
To be able to judge our level of success we need a yardstick for comparison. We need to be able to measure our performance. This yardstick could be almost anything. It could involve numbers, an outcome or a goal. For example, you might like doing push-ups. You might set 50 push-ups as your goal. You might rank performances based on a particular number of push-ups. Less than 20 is bad, around 30 is not bad, around 50 is satisfactory, more than 80 is great, and more than 100 is incredible. You might measure your success as never doing less push-ups than a previous attempt. For example, you did 32 push-ups on Monday. On Tuesday, you need to do at least 32 push-ups. There are so many possible ways of measuring success just with the simple example of push-ups.
Different people will use different yardsticks to measure their success. For one person performing 20 push-ups could be considered a success and for another person performing 20 push-ups could be considered a failure or below expectations.
Setting expectations
It is important to set reasonable expectations. Setting an expectation too high will mean we will rarely succeed. Setting an expectation too low will mean we will succeed regularly but that success will be less rewarding. Ideally, you want to set a challenging but achievable target. There needs to be at least some risk of failure or success offers very little meaning. For example, some computer games have different levels. If you are new to a particular game, winning the game on the lowest level will feel like some form of achievement. As you become proficient at playing the game, continuously succeeding at the lowest level will no longer be fulfilling. Continuously succeeding at the lowest level will stunt your ability to continuously improve at playing the game. If you play this game against your friends who have been playing at a higher level, you are less likely to be successful against them.
The importance of failure

To be able to appreciate success, we need to experience failure. Failure can be described as a negative experience. The negative experience of failure can be seen as an emotional yardstick. Without that yardstick, how can we assess how much better it feels to succeed than to fail? The more times we fail at something, the more gratifying it is to succeed.
The cost of failure affects the value of success. As the cost of failure increases, the value of succeeding increases. For example, investing in cryptocurrencies. The market price of cryptocurrencies fluctuate quite wildly. During a bear market, a cryptocurrency could lose 90%+ of its market cap. During a bull market, a cryptocurrency could increase its market cap by several 1000%. A high cost of failure deters people from attempting; thus, success becomes more scarce. For example, competing in motor racing. A very short lapse of judgement could be the difference between winning the race and dying.
Failure can also be used as a learning experience. It gives us a chance to look at what went wrong. We can assess how much of the failure occurred because of our actions, the actions of others, or our environment. We can look at what could have been done differently, if anything. Failure can be used to increase our chances of future success. Failure can also be used to reassess goals and objectives.
Third party perspective
Does third perspective of your level of success matter? I believe it matters, if you believe it does. You may design your measure of success differently than those around you. For example, two soccer teams play. Let us call them Team X and Team Y. Team X wins the game 4-2. Team Y has the lost the game. A third party could consider this loss a failure. However, Team Y could be a considerably weaker team than Team X. Team Y did not enter the game with the expectation of winning but instead to make their mark by scoring at least one goal or by not losing by more than 4 goals. If those were their objectives, they reached some level of success that may not be apparent to a third party.
Sometimes you might align your level of success with someone else’s goals. For example, you might have a job in sales. Your team has been set a goal of selling 200 widgets a week with five employees. That is an average of 40 widgets per employee. Your own goal should align in some way to the goal of your team. If you set a target of just 10 widgets a week, you are likely to achieve your goal but you are contributing very little to the team’s goal of 200. Your colleagues probably will not appreciate your efforts and your boss might fire you. If this bothers you, you should probably respect their perspective of success.
Optimal probability of success (more technical part of the post)
Is there such a thing as an optimal probability of success? If we consider success in financial terms, we can consider both expected value and expected utility. If we consider success in non-financial pursuits, we need to consider both the likelihood of success and the cost of failure.
Optimal probability of success (financial consideration)
As the risk of failure increases, the expected reward from succeeding increases. We can consider this in terms of expected value. The expected value of success can be expressed as follows:
Expected Value = α × S + (1-α) × F
Where: ‘α’ is the probability of success, ‘S’ is the return from success and ‘F’ is the return from failure.
If the probability of success is 100%, the expected value is equal to the return from success (1 × S). If the probability of success is 50%, if we assume return from failure is zero, the expected value is equal to 50% of the return from success (0.5 × S). If the probability of success is 50%, if we assume the negative return from failure is equal to the return from success, the expected value is equal to zero (0.5 × S – 0.5 × S = 0).
Most people are risk averse. Therefore, both the reward from succeeding and the expected value increase with risk. People are generally more interested in maximising their expected utility rather than their expected value. The expected utility of success can be expressed as follows:
Expected Utility = α × S^0.5 + (1-α) × F^0.5
The above equation assumes a person is risk averse. This risk aversion is demonstrated by the inclusion of ‘0.5’ in the equation. Any positive value less than ‘1’ indicates the person is risk averse. The extent of risk aversion determines the level of risk a person is willing to take to succeed. A very risk averse person will make decisions that will give them a very high chance of success even if the return/reward for succeeding is very low.
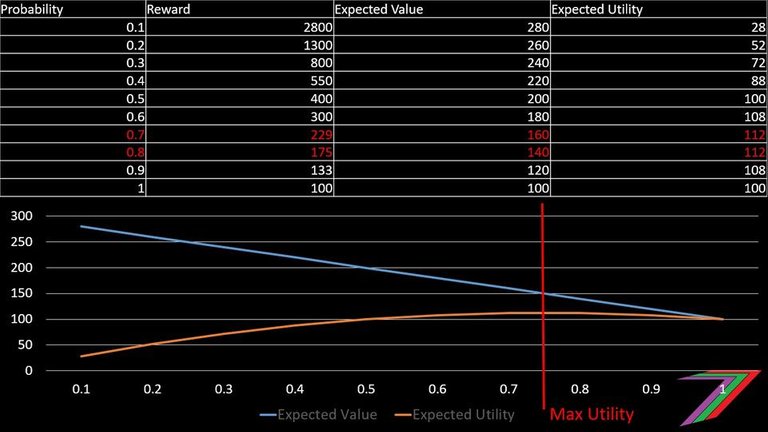
The market generally accounts for risk aversion. Therefore, high-risk investments offer high expected returns/values. Are these higher expected returns sufficient to entice people to take the risk? Figure 1 shows increasing expected returns as the probability of success falls as well as the corresponding utility obtained from these returns.
Figure 1: Optimal probability of success using expected utility
**Note: Expected value increases linearly by $20 for every drop in 10% chance of success. Utility function used equals (αS^0.5)^2. Returns and utility of failure are assumed zero.
In the above example, the optimal probability of success is 75%. This is the point where utility is maximised based on the possible expected returns at different levels of risk.
Optimal probability of success (non-financial consideration)
Is it possible to determine an optimal probability of success for non-monetary rewards? This is a very challenging question. The most desired probability of success is going to depend on the activity as well as the consequences of failure. For example, a person might choose to climb a mountain because of the very low chances of success. Reaching the top of the mountain is rewarding because it is so difficult to do. However, the consequences of failing could be death, which is a very high price to pay but also adds to the reward of succeeding. If failure is likely to result in death, the mountain climber will likely do whatever possible to decrease the chances of failure.
A possible approach to consider is to use an algorithm that determines the optimal ratio of success to failure. For this post, I have constructed a simple algorithm to demonstrate how this could be done. This algorithm is as follows:
LN(X×Sf+1) × Y / (Sf + 1)^-Z
Where: ‘LN’ is the natural logarithm, ‘X’, ‘Y’, and ‘Z’ are parameters and ‘Sf’ is the ratio of success to failure
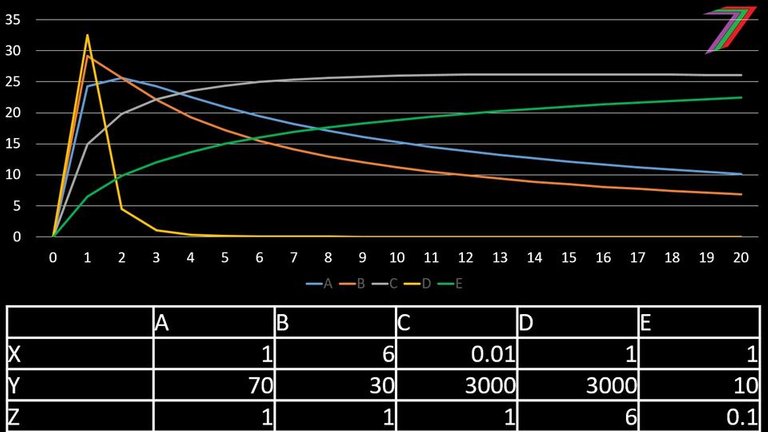
I have structured the algorithm to increase initially at a decreasing rate and then decrease at a decreasing rate but never falling below zero. The parameters determine the point utility decreases and the rate of decrease. Figure 2 contains 5 curves with different parameters to demonstrate the different possible shapes for these curves using my algorithm.
Figure 2: Utility and ratio of success to failure
Where the y-axis is utility and the x-axis is the success to failure ratio.
Curves D and E represent opposites in regards to optimal success to failure ratios. A person represented by curve D gains great value from success when the probability of succeeding is low. A person represented by curve E always wants to succeed and has the desire to avoid failure at all costs. Even someone with these characteristics will experience diminishing returns from success based on the algorithm. Success should be subject to diminishing returns unless it becomes an addiction.
The parameters applied to the algorithm need to be linked with actual behaviour and expectations. Observed behaviour and contingent valuation approaches can be used to produce inputs for determining the parameters. Actual data will also indicate if the algorithm needs to be revised to more accurately reflect information collected. A similar approach to what I describe in my posts, ‘Social Economic Utility Analysis (working title) Algorithms’ and ‘Social Economic Utility Analysis (working title) Model’ could be applied to obtain estimates for parameter values.
Summary

Success is something people desire. Success gains value when it is harder to achieve and the chances of failure are higher. If the chances of success are unrealistically high, success might be valuable but too infrequent to yield maximum satisfaction. Obtaining a balance between frequency of success and value of success is difficult. It will vary from person to person and from activity to activity. Success can also gain value if the consequences of failure are high.
In this post, I have discussed methods of determining the optimal level of success. For financial success, the use of expected values and expected utility is reasonably well documented. For non-financial related success, economics has yet to provide defensible theory and models. The algorithm I presented in this post is just an example of how this area could be further explored.
More posts

If you want to read any of my other posts, you can click on the links below. These links will lead you to posts containing my collection of works. These posts will be updated frequently.
New Economics Udemy Course

I have launched my first Udemy course ‘Economics is for Everyone’. The course focuses on how economics affects everyday people, the decisions they make and how they interact with the world around them. The course contains 24 video lectures (about 4 hours of viewing), 64 multiple-choice questions (3 at the end of most lectures), 32 downloadable resources (presentation slides, additional notes and links to relevant Steem posts), and 2 scenario questions. The course is currently free-of-charge. Click the link above to access the course.




Steem - The Future of DApps










You always post some useful brain twisters!
:)
Hi @spectrumecons!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 4.767 which ranks you at #1514 across all Steem accounts.
Your rank has improved 3 places in the last three days (old rank 1517).
In our last Algorithmic Curation Round, consisting of 139 contributions, your post is ranked at #116.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server
A new way for me to learn things in a different way you executed this post so perfectly
Thanks @blazing
Hi, @spectrumecons!
You just got a 1.23% upvote from SteemPlus!
To get higher upvotes, earn more SteemPlus Points (SPP). On your Steemit wallet, check your SPP balance and click on "How to earn SPP?" to find out all the ways to earn.
If you're not using SteemPlus yet, please check our last posts in here to see the many ways in which SteemPlus can improve your Steem experience on Steemit and Busy.
Wow that’s plenty of valuable info....! Thanks a lot
Posted using Partiko iOS
I'm glad you found it useful.
@spectrumecons, In my opinion, when it comes to this material world then success is, achieving all the needs for us and for our family and then after that if still we are able to contribute towards other's life and society is true success.
Posted using Partiko Android
That's a really nice goal to have.
👍👍
Posted using Partiko Android