Introduction to Algorithms
Algorithms are the heart of problem-solving. Algorithms makes the solution to any particular problem a possibility.
The birth of typography led to the birth of computers, in order to use computers to their full potentials algorithms need to be created to solve particular problems and get us through specific processes.
Mathematical solutions like the decimal system were really huge discoveries as at the time they were introduced and this was because the decimal system helped in no small means in solving the problem of taking count of numbers.
The precise and efficient nature of the decimal system makes it fit to be called an algorithm.
Since the invention of the decimal system we have seen as a result, an immense boost in different areas and ways of life. Just by providing a way to keep track of numbers and manipulate them efficiently we have been able to give birth to a whole new world being floated as Western civilization.
The Fibonacci Algorithm
The Fibonacci sequence really needs no introduction to math junkies, it is almost as popular as pizza.
The Fibonacci sequence simply explained is a list of numbers where each number on the list is gotten as a result of adding its two preceding numbers.
The formula for deriving the next number in a Fibonacci sequence can be illustrated as thus
We can also say that
In the first image illustrated, it tells us that for an unknown Fn if n > 1 we need to apply the formula, if n = 1 or 0 then Fn is also equal to 1 or 0 respectively.
When applying an algorithm like the formula to the Fibonacci sequence, three very important factors need to be considered in order to determine whether the used technique is the best approach for that particular process.
First we'd need to ask ourselves and determine whether the eventual final result is correct and desired. If the desired result is gotten then we can say that is the right algorithm to use. But we cannot be 100% sure yet until we have considered the remaining factors.
Secondly, we need to calculate the time it will take for this particular algorithm to solve problems depending on characteristics of the problem which we can regard as a function of n, and n is the subject of the problem being addressed.
If for example, we find out that the time calculated is greater than or equal to the Fn we can see obviously that the chosen algorithm is a bad choice for solving the problem and this is because the scenario explained shows that the more n increases the more we can count on the time to increase too.
Assuming we find out otherwise and n does not relate with the time adversely we can deduce that this is the right choice of algorithm, then we can consider the third factor.
Lastly, we would need to take a look at the algo intimately, study all its moving parts and decide if there is an obviously better way that can make this algorithm more efficient, precise and less time consuming.
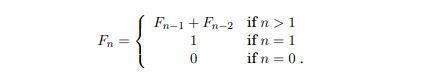
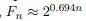
Hi, @gotgame!
You just got a 0.18% upvote from SteemPlus!
To get higher upvotes, earn more SteemPlus Points (SPP). On your Steemit wallet, check your SPP balance and click on "How to earn SPP?" to find out all the ways to earn.
If you're not using SteemPlus yet, please check our last posts in here to see the many ways in which SteemPlus can improve your Steem experience on Steemit and Busy.
Congratulations @gotgame! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!