En los procesos desarrollados anteriormente en mi post sobre Límites Infinitos, se hizo mucho énfasis en observar el comportamiento de la Función Recíproca f(x)=1/x (con x diferente de 0) cuando x se aproximaba a 0 tanto por la izquierda como por la derecha; luego de la observación concluimos y afirmamos que cuando x se aproxima a 0 por la izquierda f(x) decrece ilimitadamente y que cuando f(x) se aproxima a 0 por la derecha f(x) crece ilimitadamente y, además, que a través de este proceso se permite identificar, en este caso, la asíntota vertical x=0.
Ahora analizaremos el proceso contrario, es decir, ¿qué pasa con la Función Recíproca cuando la variable x se aleja arbitrariamente de 0 tanto por la derecha como por la izquierda?; es decir, cuando x crece o decrece ilimitadamente.
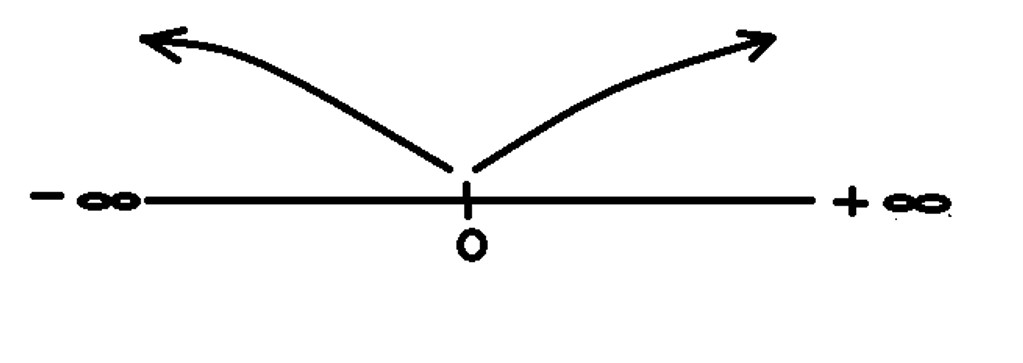
Nos estamos refiriendo en este caso a:
Para analizar esta situación nos valdremos de dos tablas de valores con lo cual trataremos el caso.
Comencemos:
Tabla 1
Tomaremos valores x que se alejan de 0 por la izquierda:
| x→-∞ | f(x) |
|---|---|
| -1 | -1 |
| -10 | -0,1 |
| -100 | -0,01 |
| -1000 | -0,001 |
| . | . |
| . | . |
| . | . |
| -10000000 | -0,0000001 |
En la columna de la izquierda vemos los valores de x decreciendo en un proceso continuo e infinito y en la columna derecha están los respectivos valores que toma la función recíproca f(x)=1/x para cada valor de x respectivamente. Estos resultados muestran como a medida que x decrece ilimitadamente, es decir, x se hace cada vez más infinitamente pequeño, en esa proporción, f(x)=1/x se hace más próxima a 0 por la izquierda; es importante mencionar que en este caso la recta y=0 es una asíntota horizontal.
Y escribimos:
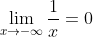.gif)
Bosquejemos la gráfica:
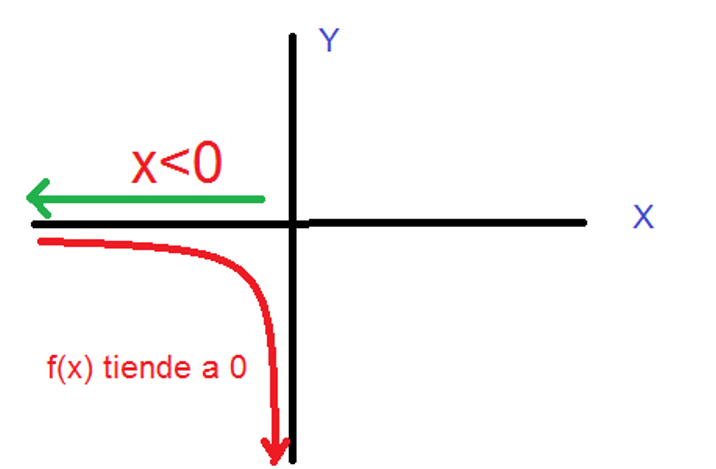
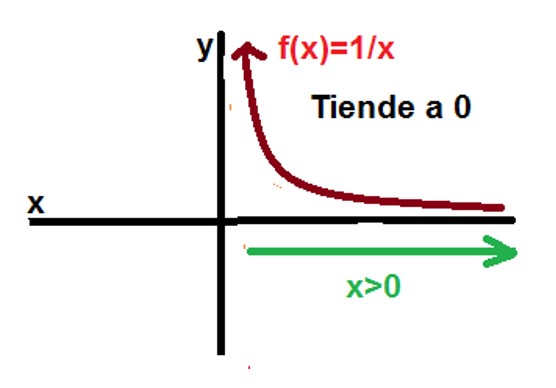
Ahora analicemos el caso cuando x tiende a 0 por la derecha.
Tabla 2:
| x→+∞ | f(x) |
|---|---|
| 1 | 1 |
| 10 | 0,1 |
| 100 | 0,01 |
| 1000 | 0,001 |
| . | . |
| . | . |
| . | . |
| 10000000 | 0,0000001 |
En este caso, la tabla es muy similar a la tabla 1, ya que solo cambian los signos negativos a positivos, y la conclusión es la siguiente: La función recíproca f(x) se hace cada vez más próxima a 0 a medida que x se aleja de 0 a través de valores positivos.
Y escribimos
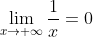.gif)
Bosquejemos el gráfico
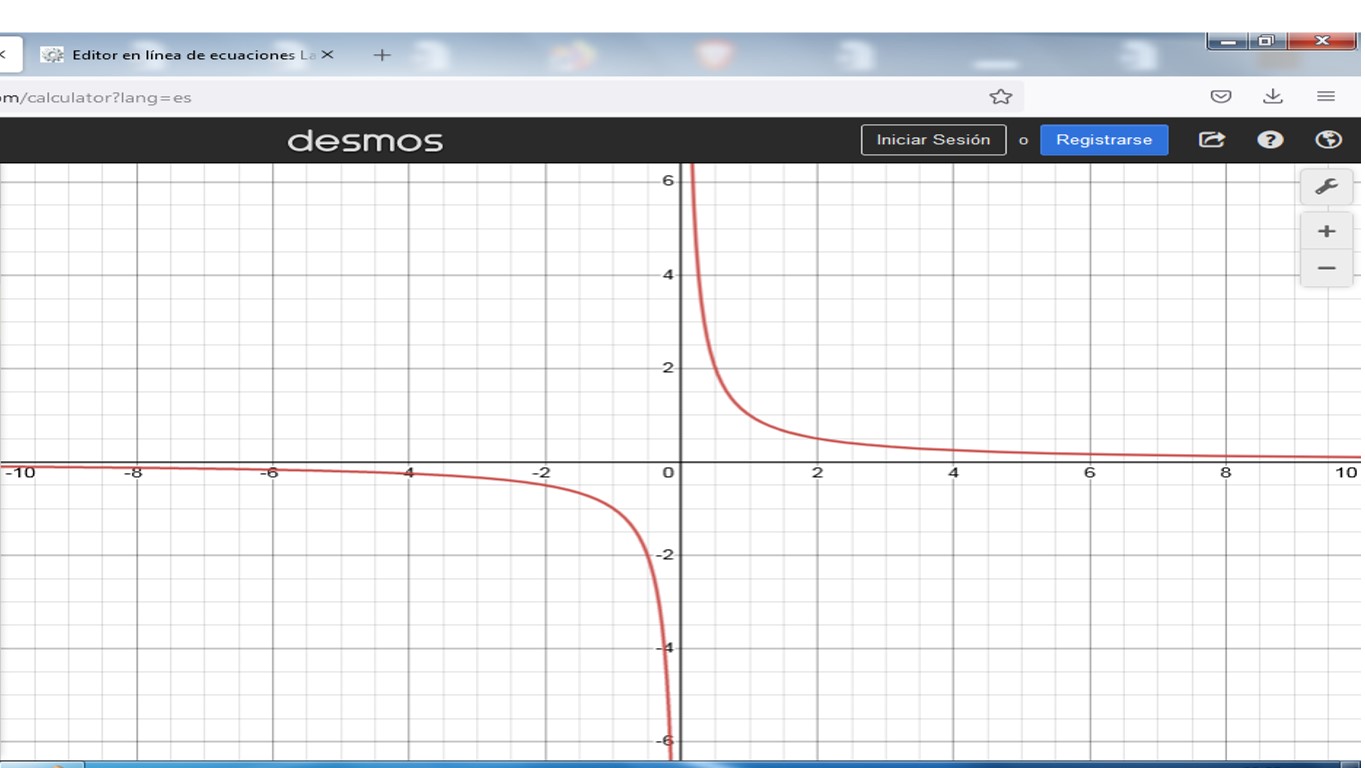
Con la ayuda en línea de la Calculadora Gráfica Desmos, aquí tenemos la gráfica integrada.
Conclusiones
A través de estos límites se puede determinar el comportamiento de una función cuando los valores de x crecen o decrecen ilimitadamente, además identificar las rectas horizontales a la cual la gráfica de la función es asintótica, es decir, las rectas horizotales a la cual la función se acerca ilimitadamente pero sin llegar a tocarla, en este caso y=0
Créditos
Mis soportes ténicos para la realización de este post fueron: Paint, PawerPoint y Desmos Calculadora Gráfica
