Integración por sustitución trigonométrica
Saludos Comunidad
Considerando que la situación actual afecta el desenvolvimiento regular de la actividad vivencial escolar en todos los niveles educativos trasladándola del aula al hogar bajo las directrices emanadas de las instituciones escolares, se hace necesario el aporte de quienes ostentamos experiencia docente en las diferentes áreas del conocimiento; esto a través de la vía electrónica, ya que es esta la forma o herramienta táctica para ello; todo esto en plan de colaboración a la sociedad.
Particularmente soy profesional de la matemática y en tal sentido en esa área será mi aporte.
En mi post La integral indefinida de la función Valor Absoluto desarrollé la integral de una función valor absoluto, siguiendo esa misma lógica, continuaré aportando sobre este tema hasta que crea necesario cambiarlo.
El tema a desarrollar hoy es:

Imagen tomada de Pixabay
Integral por sustitución trigonométrica
Este tipo de integración se aplica cuando el integrando tiene cualquiera de estas tres formas:
en este caso se introduce una nueva variable θ tal que x=asenθ
en este caso x=atanθ
en esta oportunidad el camio de variale será x=asecθ
A continuación un ejemplo de aplicación:
Calcule la siguiente integral:
Esta integral se puede reacomodar así: 
Se observa que el integrando tiene la segunda forma, por lo tanto:
x= √2tanθ→ dx= √2 sec2θdθ
Luego:
Donde:
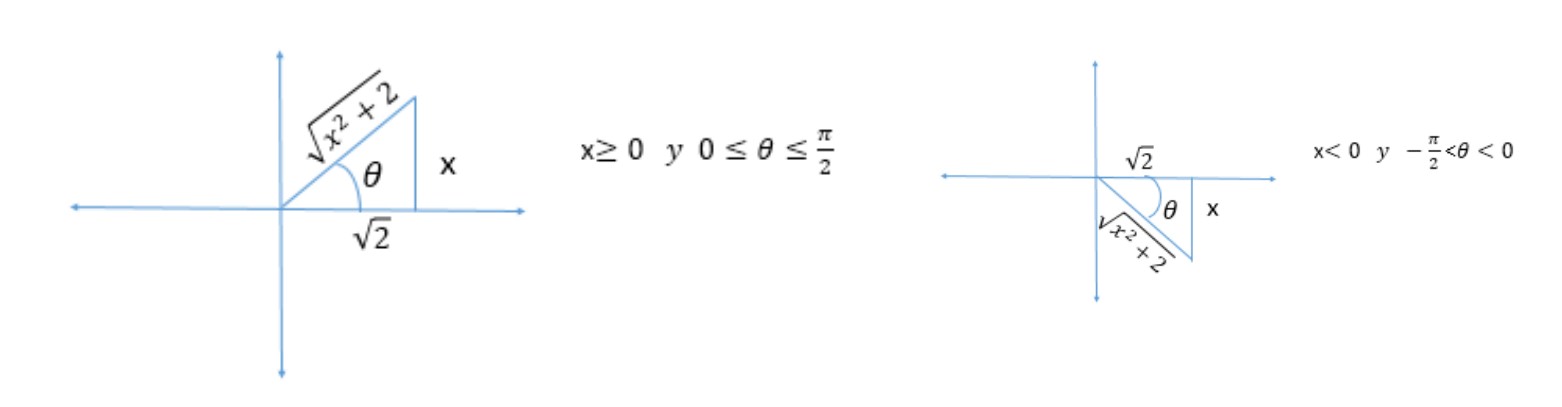
Luego:


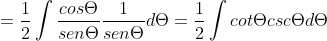

Finalmente haciendo uso del recurso de los triángulos dados, se calcula el seno del ángulo θ
Esto es: senθ =

Sustituyendo este valor en el resultado anterior se obtiene el resultado definitivo de la integral:

Créditos:
Las ecuaciones fueron realizadas con el editor de ecuaciones LaTex.



muy interesante, me costo entenderlo porque matematica la aprobe hace años en la universidad y actualmente no lo aplico.