Iniciando el concepto de ecuación en niños a partir de 11 años/Una alternativa para la enseñanza guiada del concepto de “Ecuación lineal”, en casa (parte 1)
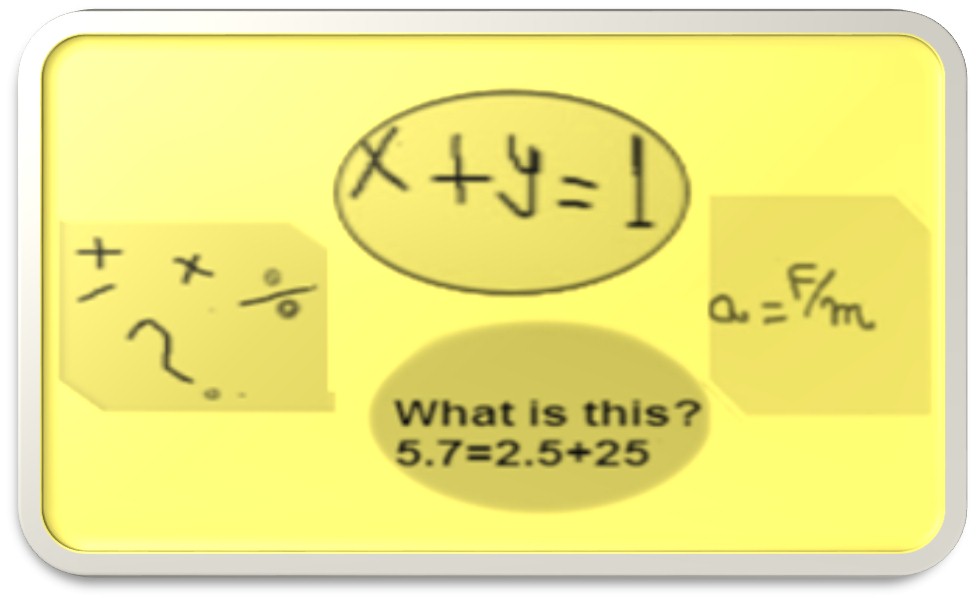
Una de las mayores dificultades (de acuerdo a mi experiencia como docente del área) que presentan los niños en el proceso de transición de la aritmética al álgebra es el concepto de ecuación lineal en una variable.
Entre las causas que he encontrado e inciden en esta problemática se encuentran los siguientes: el uso de las letras, el uso de la igualdad y el uso de los signos de las operaciones y sus propiedades.
Los alumnos presentan dificultad en el uso de las letras en el contexto del álgebra porque se han acostumbrado al uso de las letras en aritmética.
Considero que existe en aritmética una forma errónea de usar las letras que hace que se desarrolle en el alumno obstáculos para la comprensión del álgebra.
También influye en esta problemática el uso del símbolo de igualdad (=), por mi experiencia al atender niños que vienen de la primaria al bachillerato he observado que los alumnos de primaria ven el signo de igualdad como una orden para hacer algo, no lo denotan como una equivalencia donde el lado izquierdo debe equivaler al lado derecho, de tal forma que expresiones como esta: "2.4+5= 7+6", no tienen sentido para ellos.
En cuanto al uso de los signo de las operaciones y sus propiedades, se debe considerar que aprender álgebra requiere el conocimiento y manejo de las leyes y principios que rigen la aritmética ya que él álgebra elemental se rige por estos mismos principios y leyes. La diferencia entre álgebra y aritmética radica en que en aritmética se trabaja en el plano concreto (2 manzanas, por ejemplo), en álgebra se pasa al plano abstracto (2x, por ejemplo).
A continuación se presenta de manera ilustrada los tipos de usos que se le dan a las letras en aritmética:
a.-El uso de las letras como etiquetas
Al designar la altura de un triángulo se acostumbra usar la letra h que viene siendo la inicial de la palabra “altura” en inglés; es decir, se usa la inicial de la palabra para denotar objetos. Existen infinidad de ejemplos de este tipo ya que el fenómeno es muy común y rutinario en la escuela. Por ejemplo cuando designamos una longitud por “L” una circunferencia por “C.
b.-Usar las letras como objetos
Un ejemplo típico es el siguiente, si la letra a representa manzanas entonces la mayoría tienden a interpretar que la expresión “5a “, significa “5 manzanas” cuando en realidad significa una multiplicación de “5 por la cantidad a de manzanas”.
c.- Usar las letras como variables
En la mayoría de los casos se tiende a usar la x e y en el contexto de las ecuaciones.
d.- Uso de las letras como constantes
Las letras también se usan como constantes en fórmulas determinadas como por ejemplo en la física, la química, entre otras.
En cuando al signo de igualdad (=) se acostumbra al alumno a considerarlo como una orden para hacer algo, por ejemplo: 3.2+7= ; y no se le hace ver que la igualdad significa equivalencia "lo que está al lado izquierdo de la igualdad debe equivaler a lo que se encuentra en el lado derecho" de tal forma que una expresión como esta: 3.4+8=10.2, no tiene sentido para ellos.
En cuanto a las operaciones sus signos y operaciones.
En aritmética se trabaja con números naturales, vale decir: 0 (que significa ausencia de cantidad), 1, 2, 3,….; son números que sirven para contar y en tal sentido se definen las operaciones de suma (+), resta (-), multiplicación (.) y división (÷).
De acuerdo a cada operación se definen ciertas propiedades, una de ellas es la “cerradura”, esta propiedad nos dice que tanto la suma como la multiplicación de números naturales siempre da como resultado otro número natural; por ejemplo los números 2 y 5 son números naturales, entonces tanto 7 y 10 también lo son, ya que 2+5=7 y 2.5=10.
Cada una de estas operaciones posee una operación opuesta, vale decir la resta y la división que son las opuestas de la adición y multiplicación respectivamente, por ejemplo si se quiere restar 2-5 nos da -3 (un número entero negativo) el cual no es un número natural, y si se quiere dividir 2÷5 no da 0.4, obviamente 0.4 no es un número natural, más precisamente es un número racional.
Como se dijo anteriormente, cada operación en los números naturales tiene su operación opuesta, por ejemplo la opuesta de la suma es la resta su resultado es la diferencia), y la opuesta de la multiplicación es la división (su resultado es el cociente); estas operaciones opuestas no cumplen las propiedades de sus operaciones originarias por eso no cuentan en la siguiente tabla
Veamos:

Ejemplos:
Dados los siguientes números: -1, 0, 1, 11, 0.5, -4.7, 8, 16
1.-Cuáles de ellos son números naturales?
Respuesta: el 0, 1, 11, 8 y 16 son números naturales
2.-Considerando a=11, b=8 y c=16, usa el cuadro anterior para verificar las operaciones con sus propiedades.

Tomando el modelo los ejemplos anteriores se pueden realizar en casa, otras actividades que involucren las propiedades descritas.
Congratulations @analealsuarez! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz: