CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO
La palabra continuidad está directamente vinculada con la idea cotidiana de procesos que continúan; por otro lado, su contrario, la discontinuidad, se relaciona con procesos interrumpidos.

En matemática tiene esa misma connotación, solo que, los procesos en cuestión están descritos algorítmicamente continuos en el caso de la continuidad, y por la ruptura de ese algoritmo, en el caso de la discontinuidad.
Para ejemplificar estas ideas desde el punto de vista formal, observemos las gráficas siguientes:
Nota: Esta primera gráfica fue tomada de mi post sobre Límites Unilaterales
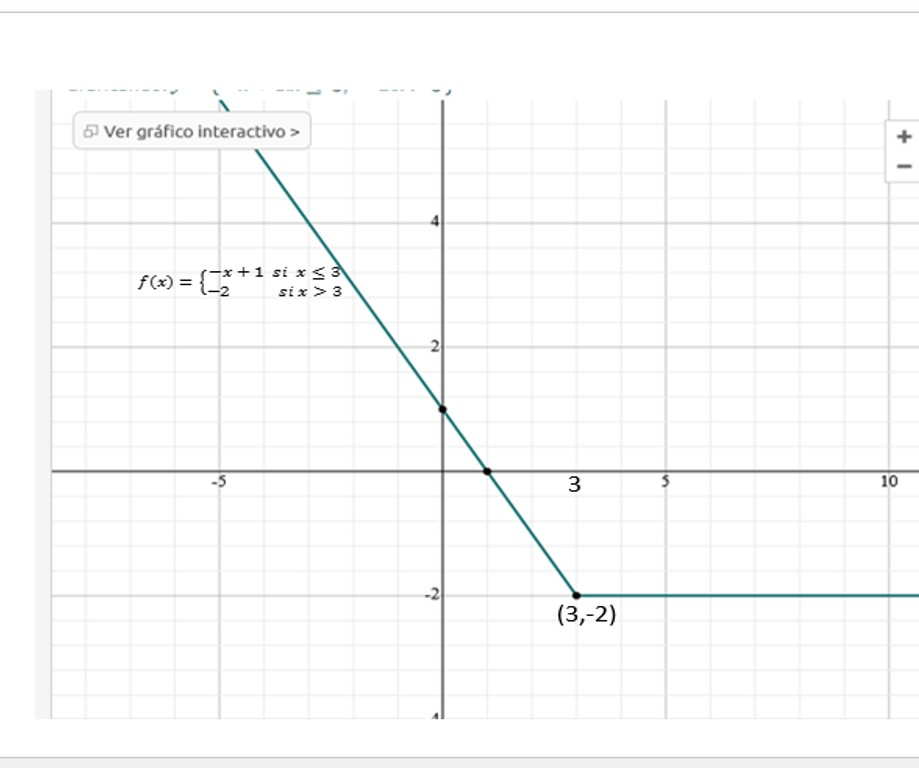
Observemos en ella, que existe un cambio del algoritmo en su definición, que de -x +3 pasa a -2 cuando la variable independiente x se acerca a 3 tanto por la derecha como por la izquierda, pero que esto no genera una ruptura por cuanto que la función está definida en x=3, y que, en este caso es -2 su imagen, es decir, el punto (3,-2) existe en su gráfico; por otro lado, se observa que el límite de f(x) cuando x tiende a 3 existe y es -2 ¿por qué?.
Definitivamente, no hay ruptura en esta gráfica, y así consideramos que es continua en x=3.
Observemos esta otra gráfica y busquemos la diferencia entre ella y la anterior.
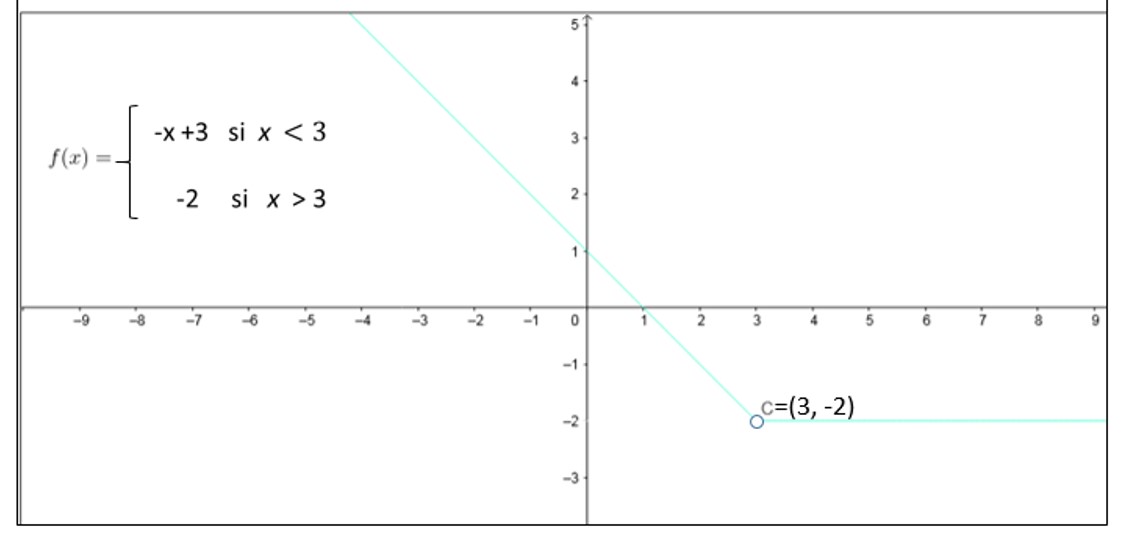
¿La vieron?
La segunda gráfica difiere de la anterior en que el punto (3,-2) no pertenece al gráfico, es decir, no existe en la gráfica de la función f y consecuentemente genera una interrupción en el gráfico, lo cual evidencia una ruptura en la gráfica en el punto (3, -2) y por lo tanto la función es discontinua en x=2.
Veamos esta otra gráfica tomada del mismo post sobre límites unilaterales
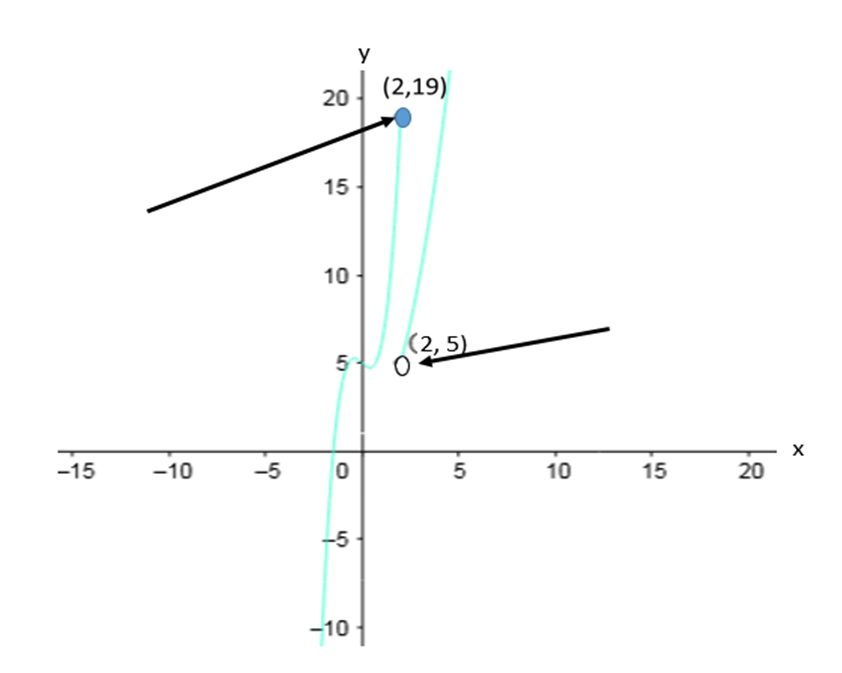
Nos preguntamos
¿Existe f(2) ?
¿Existe el límite de esta función cuando x tiende 2?
¿Hay ruptura cuando x=2?
Pues sí, hay ruptura en x=2, obsérvese que a pesar de existir f(2)=19, hay evidencia gráfica de que existe ruptura en x=2.
¿Cómo se podría explicar esto?
La explicación en este caso tiene que ver los límites unilaterales.
Estos límites son:
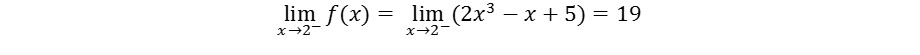
Vemos que estos límites existen, pero son diferentes, entonces el límite de esta función cuando x tiende a 2 no existe, lo cual genera una ruptura en x=2 a pesar de existir el punto (2,19) en la gráfica de f.
Finalmente, veamos esta otra gráfica
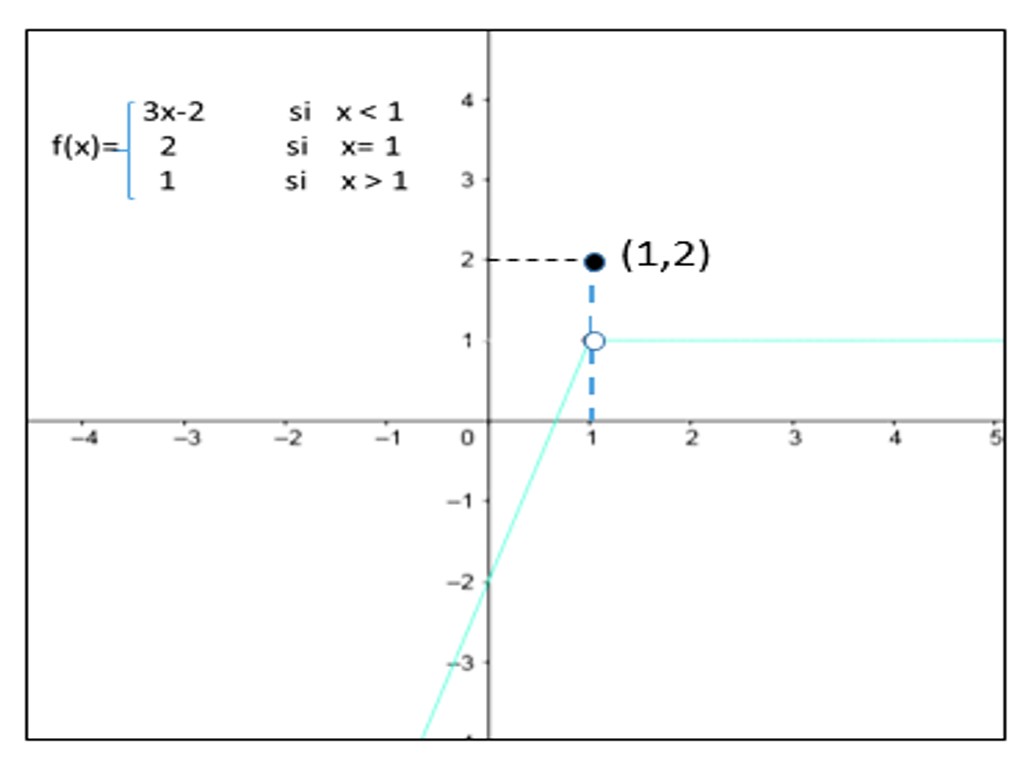
Se observa una ruptura en la gráfica de la función f cuando x=1, vemos que existe en el gráfico de f el punto (1,2) y que los límites unilaterales cuando x tienede a 1 existen y son iguales a 1.
Basándonos en estas observaciones nos preguntamos lo siguiente:
¿Cómo determinar formalmente que una función es continua o no en un punto?
Para ir introduciendonos en la formalidad de este concepto vamos a analizar en las gráficas anteriores cuáles son las condiciones que debe cumplir una función f(x) para se continua en un punto donde x=a.
En la primera gráfica vimos que el cambio de algoritmo de la función antes y después de x=3 no generó ruptura en la función; nos preguntamos ¿por qué?
En la segunda gráfica se observa que el límite de f cuando x tiende a 3 existe es igual a -2 pero, determinamos que había ruptura en x=2 ya que el punto (3,-2) no existe en la gráfica de f(x); esto es: f(3) no existe.
En la tercera gráfica f(2) existe pero se observa ruptura debido a que el límite de f(x) cuando x tiende a 2 no existe?
En la cuarta gráfica se observó ruptura en x=1 a pesar de f(1) existe y también existe el límite de la función f cuando x tiende a 1, este es igual a 1.
¿Qué debería suceder para eliminar esa ruptura?
¿Cuál de estas tres gráficas representa una función continua?
Todos coincidiremos en que la función f(x) representada en la primera gráfica es continua en x=3 .
¿Qué condiciones cumple f para ser continua en x=3?
Usando el sentido común, esas condiciones deben ser las siguientes:
(i) f(3) = -2 existe (condición que no se cumple la segunda gráfica)
(ii) El límite de f(x) cuando x tiende a 3 existe es igual a -2 (condición que no se cumple en la tercera gráfica)
(iii) El límite de f(x) cuando x tienede a 3 es -2, este a su vez es igual a f(3)=-2 (condición que no se cumple en la cuarta gráfica, ya que, el límite de f cuando x tiende a 1 es 1, y, f(1)=2, estos valores son diferentes)
Luego de este análisis sobre estas cuatro gráficas vamos a formalizar la definición de función continua en un punto.
Definición
Se dice que una función f es continua en un punto x=a de su dominio, si se cumplen estas tres condiciones:
(i) f(a) existe.
(ii) Límite de f cuando x tiende a a también existe.
(iii) Los dos valores anteriores son iguales.
A continuación dejo un ejercicio propuesto vara verificar las condiciones de continuidad para la función f en los puntos x= -1 y x=1
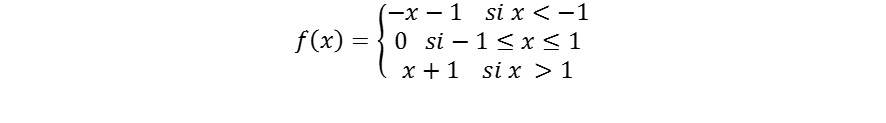
Ficha Técnica
Para la composición de la imagen de entrada se tomaron imágenes de Pixabay.
Para la construccion de gráficas matemáticas.
https://www.geogebra.org/m/dbdugjrx
https://es.symbolab.com/solver/one-sided-limit-calculator/%5Clim_%7Bx%5Cto2-%7D%5Cleft(2x%5E%7B3%7D-3x%20%2B12%5Cright)?or=input
The operators doing V2K with remote neural monitoring want me to believe this lady @battleaxe is an operator. She is involved in the same discord groups around @fyrstikken and friends. Her discord is Battleaxe#1003. Shes in some groups with seemingly detached characters that dont even acknowledge the others in the group, looking oddly staged. She starts projects and does nothing with it or the delegations after its used to sway people. Like @steempowertwins does<------fake along with her @teamgood <------fake. No substance in her comments and has a following that adores her for what? Life coach she is not nor is she insightful with any meaningful skills to follow. Ruler of pixie dust maybe? I would like for someone to show me but probably wont out fear maybe? @fyrstikken groups around him down voted me into censored and not viewable on my accounts as soon I told what they were doing.
I cant prove @battleaxe is the one directly doing the V2K and RNM. Doing it requires more than one person at the least. It cant be done alone. She cant prove she is not one of the ones doing V2K because she cant and could care less. I guarantee she knows this is going around and still wont prove it because she cant. Many of us here can prove what they have been doing to survive the past 5 years. What does she live off of? It definitely isnt in public view here.
I was drugged in my home covertly, it ended badly. They have been trying to kill me using RNM with applied V2K mental games while revealing as many accessories to the crime as they can. I bet nobody does anything at all. Ask @battleaxe to prove it. I bet she wont. Pretty serious accusations to just blow off and leave the crypto community hanging in fear of this danger.
They want me to believe the V2K and RNM in me is being broadcast from her location. And what the fuck is "HOMELAND SECURITY" doing about this shit? I think stumbling over their own dicks maybe? Just like they did and are doing with the Havana Syndrome. They should start by looking at the communications between the top witnesses of Hive and the connection to @fyrstikken groups. Google his fucking name and see where his other interests lie around at least once maybe? The connections between @fyrstikken groups and all the exchanges built for Hive? Bet that would reveal some crazy ball less nutty shit. Homeland security should start preparing for their own incarcerations seeing how sloppy this was done. Patriot act my ass. Think we are really fools? Bad position your not getting out of. Dont be last to blow the whistle. Who will protect you?
People in and around @fyrstikkens groups are reckless and should have shown the proper media what they had before taking me hostage for 5 long torturing years and counting. That is a long time to wait for someone to die.
What would you say while having a gun pointed at your head from an undisclosed location? Have people find it? My hands are tied while they play like children with a gun to my head. Its a terrorist act on American soil while some yawn and say its not real or Im a mental case. Many know its real. This is an ignored detrimental to humanity domestic threat. Ask informed soldiers in the American military what their oath is and why nothing is being done. Nobody has I guess. Maybe someone told ill informed soldiers they cant protect America from military leaders in control that have ill intent. How do we protect locked up soldiers prevented from telling the truth from being treated as criminals? Not to mention civilians we let our leaders treat the same way. https://ecency.com/fyrstikken/@fairandbalanced/i-am-the-only-motherfucker-on-the-internet-pointing-to-a-direct-source-for-voice-to-skull-electronic-terrorism-terrorism
Su post ha sido valorado por @ramonycajal