Gradient Decent for Learning
This post, similar to the previous one, will focus on how a neural network can be used to identify handwritten digits. This is a very popular introductory problem to neural networks. You could call it the "Hello World!" problem for the field of neural networks.
This is the fourth post in a series on neural networks and deep learning. This series is my attempt to get more familiar with the topic and is heavily based on the book by Michael Nielsen.
This network to classify handwritten digits will take digital scans of single digit numbers. The grayscale, 28 by 28 pixel images of scanned handwritten digits are used as input to a neural network of which the output is a number between 0 and 9. The grayscale value between 0.0 and 1.0 of each pixel is used as an input to the input layer of neurons. Hence, the input layer consists of $28 \times 28 = 784$ neurons. To train the network, a data set provided here is used. This set contains a 60,000 training sets and 10,000 test sets. A set contains both the images and the digits they are representing. The data can also be found in the repository where we will eventually build the digit-recognition tool in the coming posts.
As done in the book, we will use $x$ to denote a training input. Given the pixel size of the images, it is convenient to define the pictures as vector with length $28 \times 28 = 784$. The elements in this vector contain a value that represents the grayscale value of the corresponding pixel. We'll denote the output of our digit recognitionn tool $y = y(x)$. $y$ will be a vector of length 10 and it contains all zeros except one element. This one element contains a one. The non-zero element location in $y$ represents the value of the input digit. According to the neural network, that is. The example output for a digit of 6 would be the following:

Note that the first entry corresponds to the first digit, i.e., 0!
The first thing needed is an algorithm that gives us the weights and biases of our network, such that the output of the network approximates $y(x)$ for all the inputs $x$ from our training set we feed into the network. To measure how well our algorithm achieves this goal we need a metric. For this, we define a cost function:
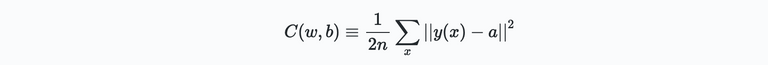
Here $w$ and $b$ represent all the weights and biases of the network, $n$ the total number of inputs, $a$ is the vector of outputs of the network given $x$. Note that $a$ depends on both the weights and biases, as well as the input $x$. The straight brackets $||\cdot||$ is the L2 or Euclidean norm of a vector. $C(w,b)$ is also known as the quadratic cost function or *mean squared error$ (MSE). A few important observations when looking at the cost function:

The obvious conclusion is that our, to be designed, algorithm performs well, when $C(w,b)$ is small, or $C(w,b)\ll0$. So in other words, the aim of our training algorithm is to minimize the cost as a function of the weights and biases in the system. To do this we use an algorithm that is known as gradient descent.
So what do we use the quadratic cost function? Another option would be to just maximize the number of correctly classified images by the network. However, this metric is not a smooth function of weights and biases, and optimizing this is tricky. Small changes in weights and biases wont improve the algorithms performance at all in the majority of cases. It would be hard to figure out how to adjust the weights and biases. With the smooth quadratic cost function, it turns out to be quite easy to achieve this. Hence the reason we will be using them in this work first. Once we gain a bit more understanding on this matter, we will be looking at the cost function a bit more in depth and improve it's performance with some modifications.
So at this point we have been given a "simple" quadratic function that somehow helps us train a network. We have weights, biases, a network architecture, $\sigma$, the data itself. How do we obtain a well working neural network that does what we want?
Before going moving on, let's just focus purely on our cost function and forget the rest for a bit. We will be looking at the other pieces of the puzzle later. The main idea here is that we want to minimize a function of many variables. To minimize this function we use gradient descent.
Let's start with defining a function $C(v)$, where $v=v_1,v_2,...v_n$. Here $v$ is a set of many variables. Although this function consists of many variables, it is convenient to think of this function as a function of two variables only. E.g. $C(x,y)$ as shown below:
We want to find the global minimum of this function. Global here simply refers to the lowest possible value the function can get to. You can imagine dropping a ball onto this function. The point where it will roll to is the eventual global minimum (assuming the given function in the picture). This is mental experiment is nice for the simple 2D case, however, some neural networks consists of billions of weight and biases. Sketching a mental image in such case is tricky!
Ok, so let's assume we pick a point on the function and we move a very small stem in a certain direction, then the chance of of our function $C$ would be:

Here $\Delta C(v)$ is the change of $C$ due to the incremental change of $v$ defined by $\Delta v$. $\nabla C$ represents the gradient of our function $C$. Now that we have an expression for a change in $C$, we can figure out how to increment $v$ such that $C$ reduces (i.e., to get $\Delta C$ negative):
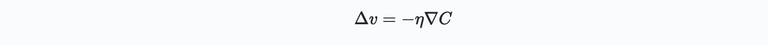
where $\eta$ is a small positive number sometimes known at the learning rate. Using the expression for $\Delta v$ in the previous expression for $\Delta C(v)$ gives:
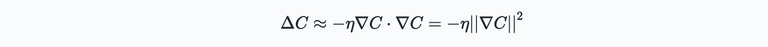
Since the squared norm on the right is always greater than or equal to zero, the minus sign above implicates $\Delta C \leq 0$. Hence, this way $C$ will always decrease. Or in other words, if we update the initial point on our function in the direction of $\Delta v$ which satisfies the above, we will eventually find our minimum! Or: $v\to v' = v - \eta \nabla C$. The choice of $\eta$ determines how big the steps are that we take with each update. Small steps means the chance we are not accidentally moving back uphill is unlikely. However, too small steps means that we need to update the location on the curve many times before finding the minimum. There are many nice ways to determine the right value for $\eta$, which will be discussed later.
For now it is enough to understand the basics above. Additionally, note that the above logic can be applied to functions of higher dimensions too!
Ok that's it for now! In the next post we will be looking more into gradient descent. It's a powerful tool, but there are some pitfalls!
Previous Articles on Neural Networks
See also my previous articles on the topic:

Congratulations @michelmake! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz: