Artificial Neurons: Perceptrons
This is the first post in a series on neural networks and deep learning. This series is my attempt to get more familiar with the topic and is heavily based on the book by Michael Nielsen. I am obviously not an expert or whatsoever. I'm merely writing these posts to share and document my learning experience. Any comments are welcome!
A perceptron is an artificial neuron. Although in machine learning Sigmoid neurons are more commonly used, it is still useful to have a look at perceptrons.
A perceptron takes multiple binary inputs and returns a single binary output. A schematic of a perceptron that takes 3 input signals is shown below:
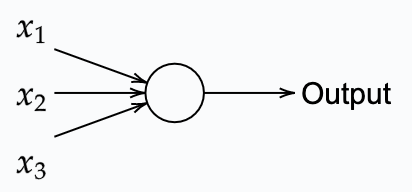
Using a set of weights w_j for each input x_1, the output of a perceptron is defined as follows:
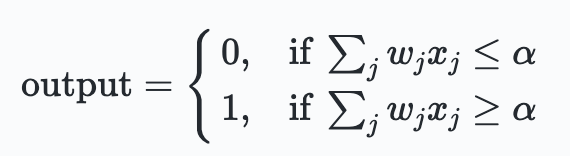
Hence the perceptron has output 1 if the combined weighted value of the inputs exceeds a given threshold alpha.
You can think of a perceptrons as simple input based decision makers. A simple example in which you could use a perceptron is to decide you need to wear a jacket when you go out. Given the following, a decision can be made:
- x_1: are there rainy clouds in the sky?
- x_2: is it hot?
- x_3: is it windy?
Based on this binary input, a decision can easily be made. If you happen to not care about getting wet from the rain, a higher weight $w_1$ is given to the corresponding input x_1 variable in the equation above. Modifying the threshold can significantly affect the decision making.
For example lets say you don't mind rain to much, the weight on the first input is set to $6$. Additionally, the weights for for the heat and wind are set to 2 as you do not like either of them. In this situation, setting the threshold to 5 or 7 would lead to different decision making.
From the above, it shows that a perceptron can be a useful as a decision maker. Of course, a single perceptron is not very useful in making complex decisions. Combining multiple perceptrons in a larger network as shown below could, however, be used for more sophisticated decisions making.
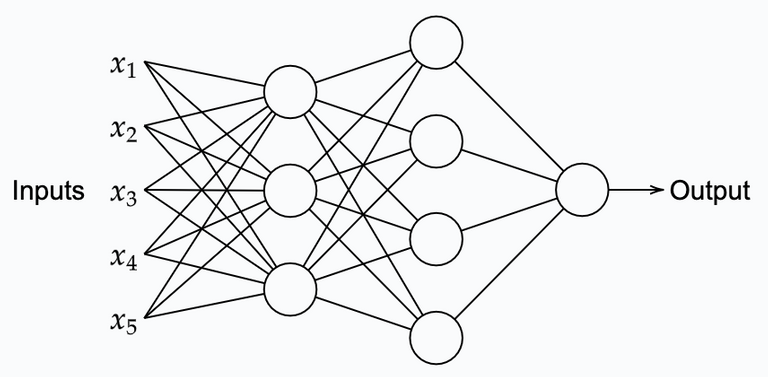
In the above, the first layer of perceptrons is making a decision based on 5 input variables. The second layer of perceptrons makes a decision based upon the output of the first layer of perceptrons. Hence, the second layer of perceptrons can make decisions on a more abstract sophisticated level. And it even more so, it holds for the third and final layer in the network. Note, in this network, the output of a single perceptron is used as input for multiple perceptrons.
To rewrite the conditional behaviour of the perceptron in the perceptron equation a dot product can be used:

In this case, the threshold alpha is replaced by the so called bias, b = - alpha. The bias controls how quickly a perceptron's output will switch from 0 to 1 by simply adding an integer to the combined value of the weighted inputs. Similarly a weight can do the same for a single input.
In simplified words, the bias determines how quickly the perceptron fires. A very large bias will allow the perceptron to fire easily, while a very negative bias will do the opposite.
A perceptron can also be used to construct computational functions such as an AND or OR gate. For example:
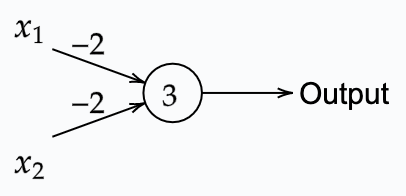
This perceptron is set with weights -2 for both inputs and a bias of 3. Hence binary inputs yields the following outputs:

This fact gives us the ability to construct any logic function simply using perceptron with the right weights and biases. Below you can see a logic design which adds two bits by a adding them and giving the carry bit if it exists:
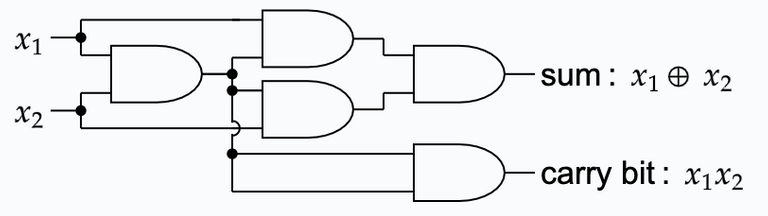
This logic can be constructed using a small network of perceptrons to:
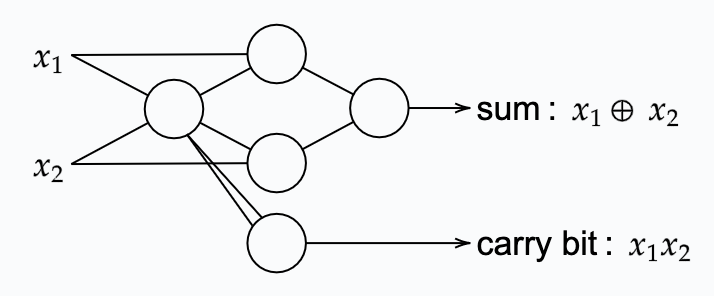
Note, that in the above network the output of one of the perceptrons is used as input twice for a single other perceptron (the one that sets the carry bit). Hence, when looking at the table of outputs for the perceptron with weights and bias w_{i,j} =-2 and b=3 respectively, this double input simply results in a bit flip. This double input can be interpreted as using a single input with w_1 and b=3. Hence the whole network would then look as follows:
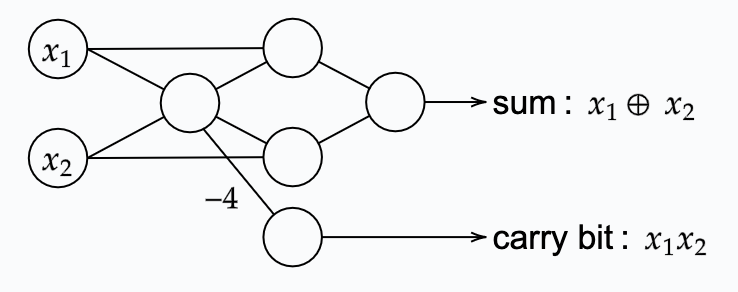
Here, the input variables are also drawn as perceptrons that simply have no input. This has no particular meaning other than the indication that these are inputs at the input side of the network.
To conclude...
From the above, it seems as if artificial neurons such as the perceptron, didn't really bring us closer to the complex task of digit recognition. However, as it turns out, it is possible to design learning algorithms, which automatically "tweak" the weights and biases of neural networks in order to make more sophisticated decisions without the intervention of a human programmer.
In the next post, we will take a different approach by using something called a Sigmoid.