APLICANDO WXMAXIMA PARA RESOLVER PROBLEMAS MATEMÁTICOS DE LA OLIMPIADA NACIONAL ESCOLAR DE PERÚ

Créditos de los logos @stemsocial y @stem-espanol

Un caluroso saludo a todos los miembros de hive.blog y especialmente a las comunidades de #STEMSOCIAL y #STEM-ESPANOL. El día de hoy, les traigo un artículo referente a un problema matemático, resuelto mediante su demostración y la programación de un script en el Sistema de Álgebra Computacional (CAS) WxMaxima.

Hace algunos años tuve la oportunidad de preparar a mis estudiantes de secundaria para su participación en la Olimpiada Nacional Escolar de Matemáticas (ONEM) de Perú a nivel local. El día de hoy les comparto un problema de la fase final (nacional) de dicha competición en su edición número XIX correspondiente al año 2023, junto a su solución analítica y computacional. Sin más preámbulo, vamos con el problema.

Definimos el conjunto

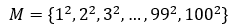
a) ¿Cuál es el menor entero positivo que divide a exactamente dos elementos de M?

b) ¿Cuál es el mayor entero positivo que divide a exactamente dos elementos de M?

Solución Parte a)

Si un entero k divide a un número p, también divide a p al cuadrado

Si k | a → k | a^2

Para todo k se cumple que k divide a k, 2k y 3k entonces k también divide a k², (2k)² y (3k)².

Luego si k ≤ 33 se cumple que k, 2k y 3k son menores que 100 entonces k², (2k)² y (3k)² pertenecen a M, es decir, todo k ≤ 33 divide por lo menos a 3 elementos del conjunto M

Ahora sabemos que 34 divide por lo menos a 2 elementos de M, estos elementos son:

34 | 34² y 34 | 68²

Solo nos falta probar que no puede dividir a ningún otro miembro del conjunto M. Cada elemento de M es un cuadrado perfecto, por lo tanto, su descomposición en factores primos puede expresarse de la siguiente forma (ecuación n°1):

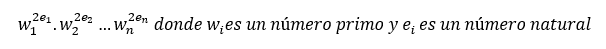
Como
34 = 2 • 17

Todo múltiplo de 34 debe tener a 2 y 17 en sus factores primos, como los factores primos de cada elemento de M están elevados con exponentes pares, entonces cualquier múltiplo de 34 en M debe ser múltiplo de 2² y 17², es decir, múltiplo de 34² y el conjunto M se denota por compresión como:

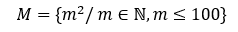
Luego se debe cumplir que

34² | m² → 34 | m

Lo cual solo se cumple para dos valores m=34 y m=68, quedando demostrado que 34 es el menor que entero que divide exactamente a dos elementos de M.

Solución Parte b)

Si un entero positivo k es el mayor divisor de dos cuadrados perfectos a² y b²

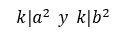
Expresando en la forma de la ecuación 1 por descomposición en factores primos

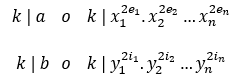
Si k divide a los números a y b entonces se cumple que a y b comparten una serie de factores primos comunes, es decir k es de la forma

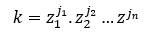
Adicionalmente, el exponente de cada factor primo z debe ser siempre par para que k sea el máximo divisor posible, ya que de no ser así habría un divisor mayor que obtendríamos al multiplicar k por dicho factor primo

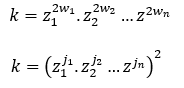
Es decir, k también es un cuadrado perfecto

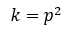
Resumiendo, hemos demostrado el siguiente teorema:

"El mayor divisor natural de dos cuadrados perfectos es también un cuadrado perfecto".

Por lo tanto, si a² y b² son cuadrados perfectos pertenecientes a M y k divide a ambos números se cumple que k es otro cuadrado perfecto luego:

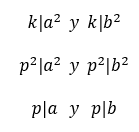
Es decir, p debe dividir a los dos enteros que generan a los elementos de M
como a² y b² pertenecen a M luego a y b son naturales menores o iguales que 100, como p debe dividir a dos números naturales menores o iguales que 100 se cumple que

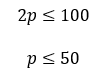
Por lo tanto, el mayor valor que puede tomar p es 50 luego

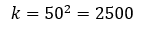
Siendo 2500 el mayor entero positivo que divide exactamente a dos elementos de M, específicamente divide a 50² y 100².

SOLUCIÓN COMPUTACIONAL

Ahora resolveremos el mismo problema de manera computacional programando un script en wxMaxima con el siguiente código:

lista: makelist(i^2, i, 1, 100)$ 
n: 1$
while n <= 10000 do
(
    div:0,
    i:1,
    while i <= length(lista) do
    (
        if mod(lista[i],n) = 0 then div: div + 1,
        i: i + 1
    ),
    if div=2 then print(n),
    n: n + 1
);

el código anterior obtiene todos los números que dividen exactamente a dos de los elementos de M, generando la siguiente salida:


34
35
37
38
39
41
42
43
46
47
68
76
84
88
92
117
126
135
160
175
176
216
245
250
252
294
320
343
384
405
432
500
507
578
588
648
675
722
768
800
882
968
1058
1152
1156
1225
1250
1296
1369
1444
1521
1600
1681
1764
1849
1936
2025
2116
2209
2304
2401
2500


Observamos que el menor de los números es 34 (solución a) y el mayor es 2500 (solución b). Esto coincide con nuestra demostración. De esta forma podemos apreciar la importancia de los sistemas de álgebra computacional, permitiéndonos comprobar la solución obtenida mediante demostraciones matemáticas.