28-02-2024 - Physics - Momentum equation [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
28-02-2024 - Physics - Momentum equation [EN]-[IT]

Basic concepts
In thermodynamics it is also important not to forget the basic concepts. When we talk about the mass continuity equation we must always remember two things: mass flow rate and volumetric flow rate.
-Mass flow rate [Kg/sec]

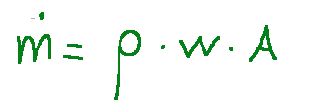
-Volume flow rate [m3/sec]

Momentum Equation
The equation representing the momentum balance (along x) is the following

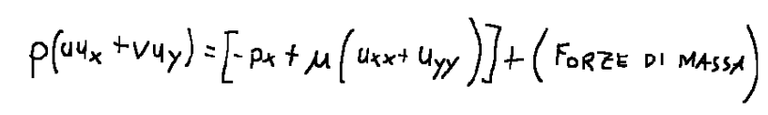
To represent the momentum equation we can use two methods:
Method 1
To explain this equation we can start from the relationship between applied forces and inertia forces, i.e. the relationship

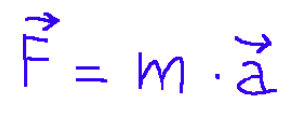
Where:
F = force expressed in N
m = mass expressed in kg
a = acceleration expressed in m/s2 (meters divided by seconds squared)
This is known as the second law of motion and we note that F and a are vector quantities. This law was introduced by Isaac Newton in 1687.

We can also express this relationship in the following way

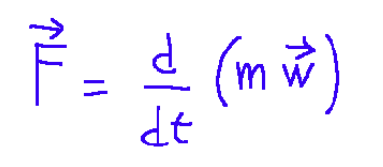
Where:
mw = momentum

Therefore mw is an extensive quantity for which the balance can be written
We then elaborate the situation taking into account using the control mass approach.
The transport theorem is then used to move on to the control volume approach.
Finally, it must be taken into account that we are in stationary conditions and that the fluid is incompressible.
The applied forces are mainly of two types: mass forces and contact forces.
In the x direction they are represented by the following term

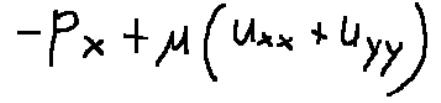
at this point we can derive the equation that represents the momentum balance.

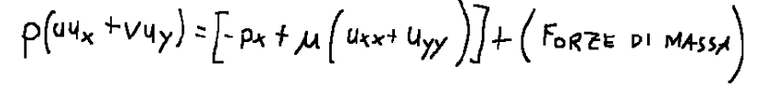
Method 2
Using the generic budget equation and taking into account the hypotheses involved we will have the following:

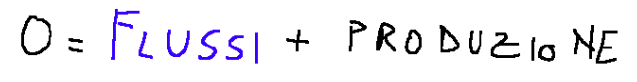
Here there are two flows at play:
the convective flow

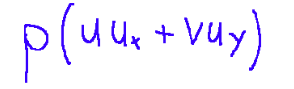
the diffusive flow

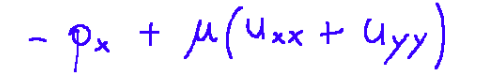
Finally we will therefore have the same solution

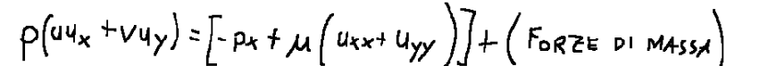
Conclusion
The principle of conservation of momentum states that if the resultant of the forces is zero then the initial momentum is equal to the final momentum.

Request
Have you ever had to do calculations where you needed the momentum balance equation? Did you remember the second law of dynamics, F = m * a?

28-02-2024 - Fisica - Equazione della quantità di moto [EN]-[IT]

Concetti base
Nella termodinamica è importante anche non dimenticare i concetti base. Quando parliamo dell'equazione della continuità di massa dobbiamo sempre ricordare due cose: la portata massica e la portata volumetrica.
-Portata massica [Kg/sec]

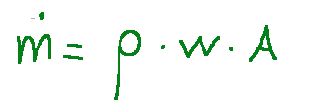
-Portata volumetrica [m3/sec]

Equazione della quantità di moto
L’equazione che rappresenta il bilancio della quantità di moto (lunga la x) è la seguente

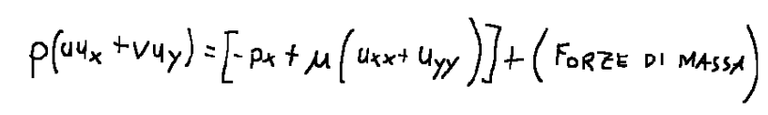
Per rappresentare l'equazione della quantità di moto possiamo usare due metodi:
Metodo 1
Per spiegare questa equazione si può partire dalla relazione tra forze applicate e forze di inerzia, ovvero la relazione

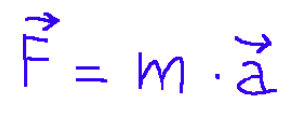
Dove:
F = forza espressa in N
m = massa espressa in kg
a = accelerazione espressa in m/s2 (metri fratto secondo al quadrato)
Questa è conosciuta come la seconda legge della dinamica e notiamo che F ed a sono grandezze vettoriali. Questa legge fu introdotta da Isaac Newton nel 1687.

Questa relazione la possiamo esprimere anche nel modo seguente

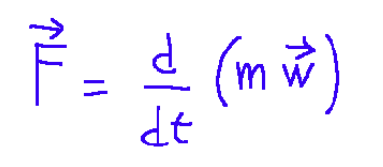
Dove:
mw = quantità di moto

Quindi mw è una grandezza estensiva della quale si può scrivere il bilancio
Elaboriamo poi la situazione tenendo conto di usare l’approccio della massa di controllo.
Si utilizza in seguito il teorema del trasporto per passare all’approccio del volume di controllo.
Si deve infine tenere conto che siamo in condizioni stazionarie e che il fluido è incomprimibile.
Le forze applicate sono principalmente di due tipi: forze di massa e forze di contatto.
Nella direzione x sono rappresentate dal seguente termine

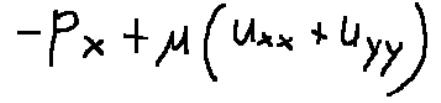
a questo punto si può ricavare l’equazione che rappresenta il bilancio della quantità di moto.

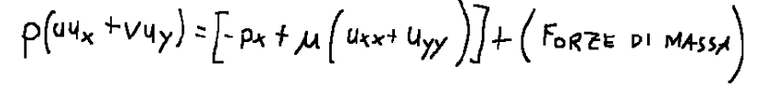
Metodo 2
Usando la generica equazione di bilancio e tenendo conto delle ipotesi in gioco avremo ciò che segue:

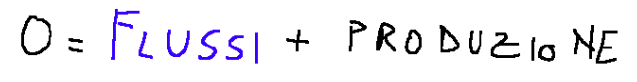
Qui i flussi in gioco sono due:
il flusso convettivo

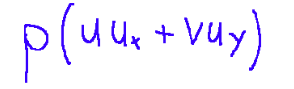
il flusso diffusivo

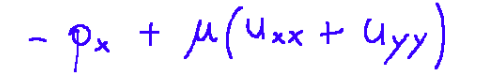
Infine avremo quindi la stessa soluzione

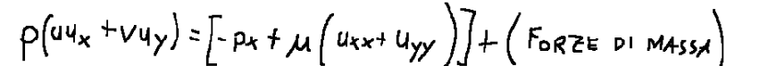
Conclusione
Il principio di conservazione della quantità di moto stabilisce che se la risultante delle forze è nulla allora la quantità di moto iniziale è uguale a quella finale.

Domanda
Avete mai dovuto fare dei calcoli in cui vi è servita l'equazione di bilancio della quantità di moto? La seconda legge della dinamica, F = m * a, ve la ricordavate?

THE END