27-11-2024 - Analytic Geometry - Orthogonal Matrices and Isometries [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
27-11-2024 - Analytic Geometry - Orthogonal Matrices and Isometries [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_63)

Orthogonal Matrices and Isometries
In analytical geometry, orthogonal matrices and isometries are fundamental concepts related to geometric transformations in Euclidean space.

Definition
A matrix

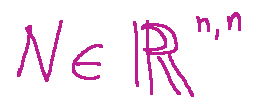
is said to be orthogonal if invertible e

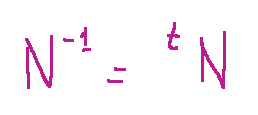
i.e. the following applies writing

The set of n x n orthogonal matrices is denoted as follows:

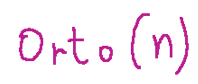
Example
The matrix representing

of the Euclidean plane centered at the origin of an angle α, that is

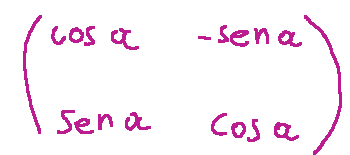
is orthogonal

Proposition
The determinant of an orthogonal matrix is ​​1 or -1

Corollary
A matrix

is orthogonal if and only if its columns form an orthogonal basis of

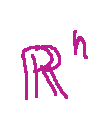
Isometric Matrices
An isometric matrix is ​​a geometric transformation that preserves distances between points. In other words, if a transformation f is an isometry, then for every pair of points P and Q:

In analytic geometry, isometrics can be represented by a combination of
-Translations
-Rotations
-Reflections
-Combinations of reflections and rotations

Conclusions
Orthogonal matrices describe linear isometrics, that is, transformations that include only rotations and reflections (without translations). An isometric matrix is ​​described by an orthogonal matrix combined with a translation vector.

Question
Do you remember studying Orthogonal and Isometric matrices at school?

[ITALIAN]
27-11-2024 - Geometria analitica - Matrici ortogonali e isometrie [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_63)

Matrici ortogonali e isometrie
In geometria analitica, matrici ortogonali e isometrie sono concetti fondamentali legati alle trasformazioni geometriche nello spazio euclideo.

Definizione
Una matrice

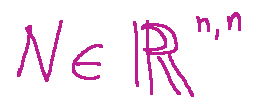
è detta ortogonale se invertibile e

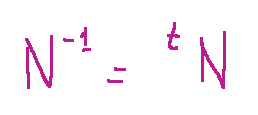
ovvero vale la seguente scrittura

L’insieme delle matrici ortogonali n x n è indicato come segue:

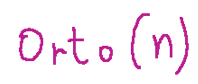
Esempio
La matrice che rappresenta

del piano euclideo centrata nell’origine di un angolo α, ossia

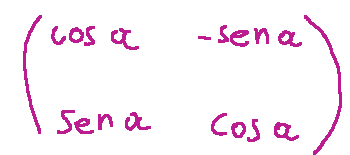
è ortogonale

Proposizione
Il determinante di una matrice ortogonale è 1 oppure -1

Corollario
Una matrice

è ortogonale se e solo se le sue colonne formano una base ortogonale di

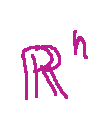
Matrici isometriche
Una matrice isometrica è una trasformazione geometrica che preserva le distanze tra i punti. In altre parole, se una trasformazione f è un’isometria, allora per ogni coppia di punti P e Q:

In geometria analitica, le isometriche possono essere rappresentate mediante una combinazione di
-Traslazioni
-Rotazioni
-Riflessioni
-Combinazioni di riflessioni e rotazioni

Conclusioni
Le matrici ortogonali descrivono le isometriche lineari, ovvero trasformazioni che includono solo rotazioni e riflessioni (senza traslazioni). Una matrice isometrica è descritta da una matrice ortogonale combinata con un vettore di traslazione.

Domanda
Ricordato di aver studiato a scuola le matrici Ortogonali e isometrie?

THE END