27-10-2024 - Analytical Geometry - Matrices [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
27-10-2024 - Analytical Geometry - Matrices [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_089)

Matrices
Considerations
In analytical geometry a matrix is ​​a table of numbers arranged in rows and columns, and represented between round brackets. The matrix is ​​used to organize numerical information in a compact and orderly way.
Below is a matrix represented.

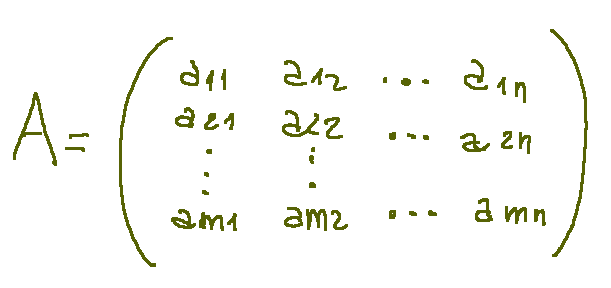
Where:
m = number of rows
n = number of columns
aij = the element found in row i and column j

Types of matrices
Square matrix where the number of rows is equal to the number of columns
Rectangular matrix where the number of rows is different from the number of columns
Identity matrix. A square matrix in which the elements of the main diagonal (from the top left corner to the bottom right corner) are all 1, and all the others are 0.
Diagonal matrix. A square matrix in which only the elements of the main diagonal are non-zero.

What are matrices used for
Represent geometric transformations (such as rotations, translations and dilations),
Solve linear systems,
Calculate distances and angles in a space.

The size of a matrix
The size of a matrix indicates the number of rows and the number of columns of a matrix. The description is as follows number of rows X number of columns.
Below is an example.

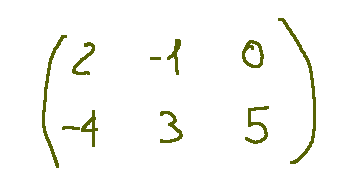
This matrix has a size of 2 X 3, in fact it has two rows and three columns

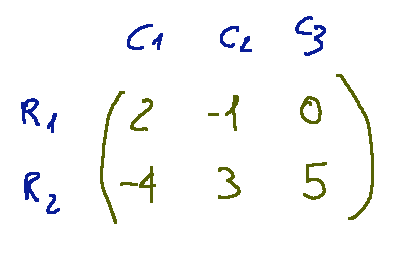
Example
Let's take the following as an example matrix

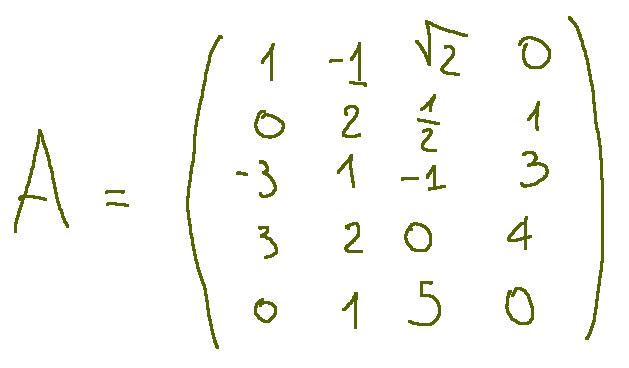
What is the dimension?
The dimension of this matrix is ​​5 X 4

A set of matrices to which A belongs
A set of matrices to which A belongs can be the next

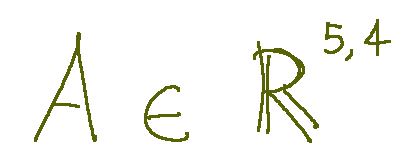
A is an element of the set R composed of 5 rows and 4 columns (the set of real numbers, i.e. the extension of rational numbers also considering numbers that can be approximated with rational numbers, such as Greek pi = 3.14159).

Conclusions
Matrices allow you to simplify and solve complex calculations in an orderly manner. This happens through specific rules and operations such as the sum, the product, and the calculation of the determinant.

Question
Did you study matrices at school? Are you using matrices in your work or in your daily life?

---

---

[ITALIAN]
27-10-2024 - Geometria analitica - Le matrici [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_089)
Le matrici
Considerazioni
In geometria analitica una matrice è una tabella di numeri disposti in righe e colonne, e rappresentati tra parentesi tonde. La matrice viene usata per organizzare informazioni numeriche in modo compatto e ordinato.
Qui di seguito è rappresentata una matrice.

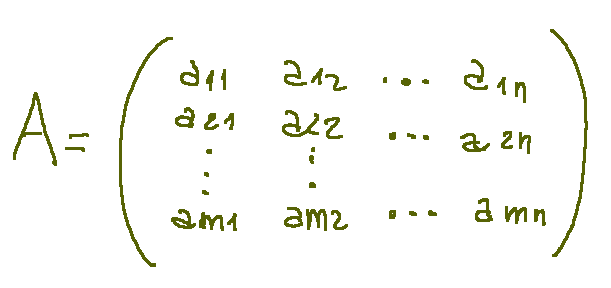
Dove:
m = numero di righe
n = numero di colonne
aij = l’elemento che si trova nella riga i e nella colonna j

Tipologia delle matrici
Matrice quadrata dove il numero delle righe è uguale a quello delle colonne
Matrice rettangolare dove il numero delle righe è diverso da quello delle colonne
Matrice d’identità. Una matrice quadrata in cui gli elementi della diagonale principale (dall'angolo in alto a sinistra all'angolo in basso a destra) sono tutti 1, e tutti gli altri sono 0.
Matrice diagonale: una matrice quadrata in cui solo gli elementi della diagonale principale sono diversi da zero.

A cosa servono le matrici
Rappresentare trasformazioni geometriche (come rotazioni, traslazioni e dilatazioni),
Risolvere sistemi lineari,
Calcolare distanze e angoli in uno spazio.

La dimensione di una matrice
La dimensione di una matrice indica il numero di righe ed il numero di colonne di una matrice. La descrizione è la seguente numero di righe X numero di colonne.
Qui di seguito un esempio.

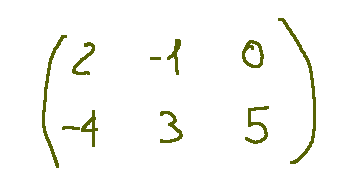
Questa matrice ha dimensione 2 X 3, ha infatti due righe e tre colonne

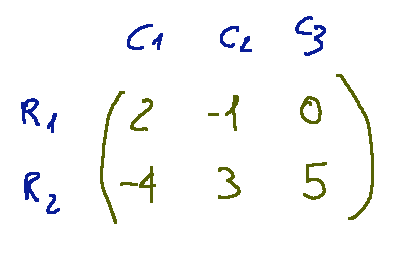
Esempio
Prendiamo come esempio la seguente matrice

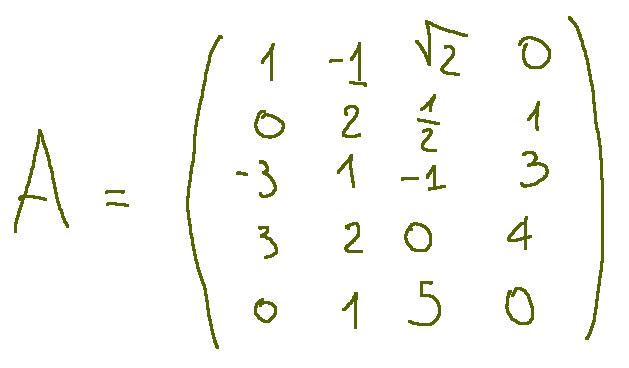
Quel è la dimensione?
La dimensione di questa matrice è 5 X 4

Un insieme di matrici a cui A appartiene
Un insieme di matrici a cui A appartiene può essere il seguente

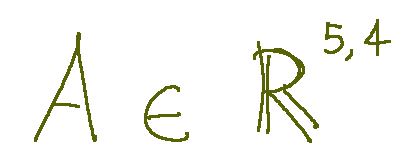
A è un elemento dell’insieme R composto da 5 righe e 4 colonne (l'insieme dei numeri reali, cioè l’estensione dei numeri razionali considerando anche i numeri che possono essere approssimati con numeri razionali, come p greco = 3,14159).

Conclusioni
Le matrici permettono di semplificare e risolvere calcoli complessi in modo ordinato. Questo avviene tramite regole e operazioni specifiche come la somma, il prodotto, e il calcolo del determinante.

Domanda
Avete studiato a scuola le matrici? State usando le matrici nel vostro lavoro o nella vostra vita quotidiana?

THE END