25-11-2024 - Analytic Geometry - Angles in the Plane and in Space [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
25-11-2024 - Analytic Geometry - Angles in the Plane and in Space [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_66)

Angles in the Plane and in Space
Angles in the plane and in space can be calculated by studying both the scalar product and the Euclidean scalar product in the plane and in space.

Definition
In the field of Euclidean geometry it is common to use a notion of scalar product that is equal to the standard one.
Given two non-zero geometric vectors v and w applied at O, the angle between them is the angle between the half-lines defined by the vectors,

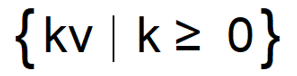
and

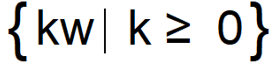
and is denoted as follows

Analysis of 2 cases
-If the two vectors are linearly independent, they are contained in a plane
-If the two half-lines are equal, the angle VW is 0, if they are not, the angle vw is π

Example
Let's try to find the geometric vectors orthogonal to the geometric vector (-1 2) that have norm 2
Let's take as a geometric vector the following geometric vector generic:

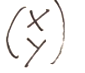
let's now identify the orthogonality condition which must be the following.

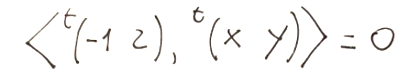
and we can also understand this as

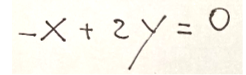
At this point we recall the Euclidean norm of our generic geometric vector, therefore the norm of

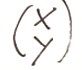
And

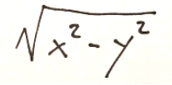
The system solution will be so

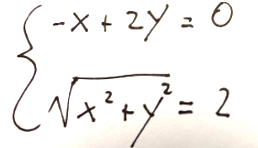
which are the two vectors sought, namely

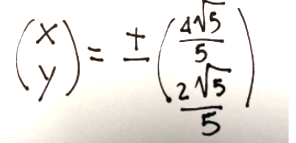
Conclusions
In analytic geometry, angles in the plane are often defined with respect to two lines or vectors, while in the three-dimensional context, angles involve vectors, lines and planes.

Question
Have you ever had to find angles in the plane and in space at school?

---

---

[ITALIAN]
25-11-2024 - Geometria analitica - Angoli nel piano e nello spazio [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_66)

Angoli nel piano e nello spazio
Gli angoli nel piano e nello spazio si possono calcolare studiando sia il prodotto scalare che il prodotto scalare euclideo nel piano e nello spazio.

Definizione
Nel campo della geometria euclidea è comune utilizzare una nozione di prodotto scalare che è uguale a quella standard.
Dati due vettori geometrici v e w non nulli applicati in O, l’angolo tra essi è l’angolo tra le semirette definite dai vettori,

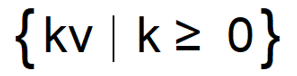
e

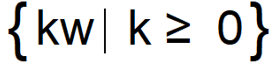
ed è indicato come segue

Analisi di 2 casi
-Se i due vettori sono linearmente indipendenti, essi sono contenuti in un piano
-Se le due semirette sono uguali, l’angolo VW è 0, se non lo sono l’angolo vw è π

Esempio
Proviamo a trovare i vettori geometrici ortogonali al vettore geometrico (-1 2) che abbiano norma 2
Prendiamo come vettore geometrico il seguente vettore geometrico generico:

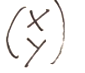
andiamo ora ad identificare la condizione di ortogonalità che dovrà essere la seguente.

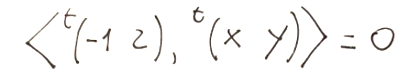
e questo lo possiamo intendere anche come

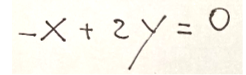
A questo punto ricordiamo la norma euclidea del nostro vettore geometrico generico, quindi la norma di

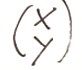
è

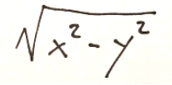
La soluzione del sistema sarà quindi

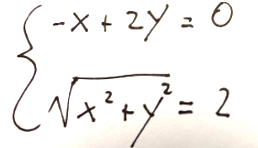
che sono i due vettori cercati, ossia

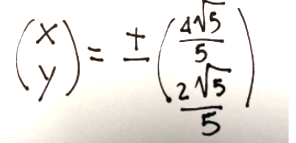
Conclusioni
In geometria analitica, gli angoli nel piano sono spesso definiti rispetto a due rette o vettori, mentre Nel contesto tridimensionale, gli angoli coinvolgono vettori, rette e piani.

Domanda
Vi è mai capitato a scuola di dover trovare angoli nel piano e nello spazio?

THE END