24-11-2024 - Analytic Geometry - Scalar Products [EN]-[IT]

avatar

image.png

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
24-11-2024 - Analytic Geometry - Scalar Products [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_67)

Scalar Products
Scalar products are useful tools to calculate angles and lengths.

Let's consider the standard scalar product on R3.
We will have the following situation

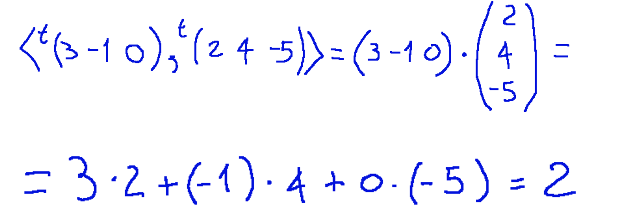
image.png

Example
Let's try to calculate the standard scalar product of the following pair of vectors.

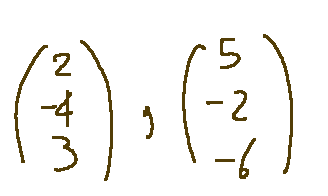
image.png

In this case we immediately identify how to calculate the scalar product between these two vectors that we will call V and W.
So the two vectors will be:
v = (v1,v2,v3)
w = (w1,w2,w3)
The scalar product is calculated in the following way:

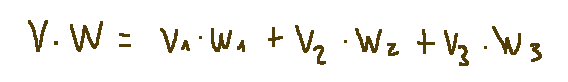
image.png

Let's remember what the vectors v and w are like

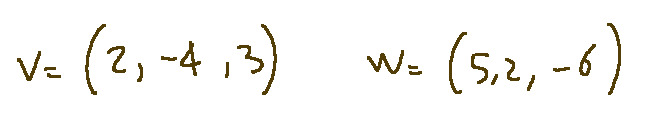
image.png

Let's now proceed with the calculation by substituting the values ​​in the first formula shown in this exercise

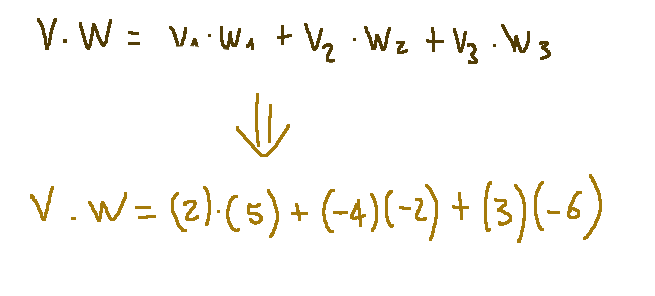
image.png

Continuing with the calculations we will arrive at this result

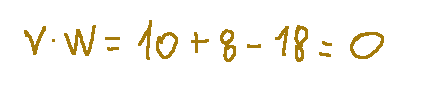
image.png

The scalar product will be so

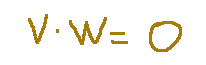
image.png

In this case we can say that the vectors are orthogonal

Example 2
Now let's find the standard scalar product of the following pairs of vectors. (1 3 0 -1) and (0 2 -1 4)

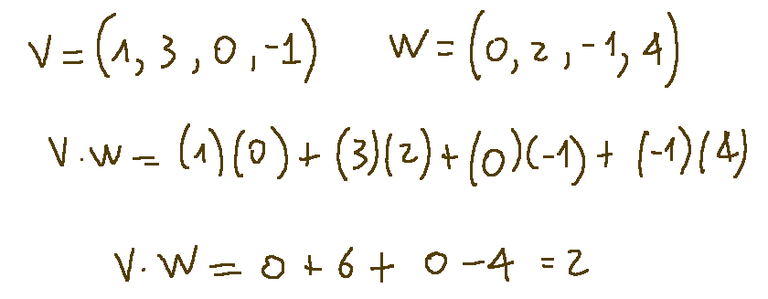
image.png
The scalar product is the following

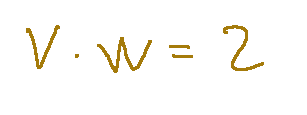
image.png

Conclusions
The scalar product between two vectors in a scalar (a number) is the basis of many other mathematical operations.

Question
Have you ever tried to do the scalar product between two vectors?

[ITALIAN]
24-11-2024 - Geometria analitica - Prodotti scalari [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_67)

Prodotti scalari
I prodotti scalari sono strumenti utili per calcolare gli angoli e le lunghezze.

Consideriamo il prodotto scalare standard su R3.
Avremo la seguente situazione

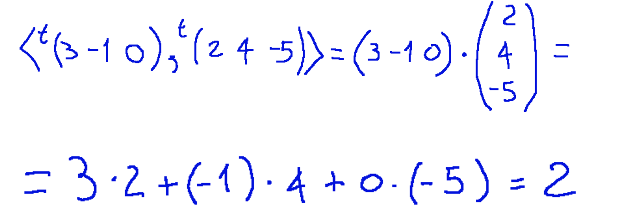
image.png

Esempio
Proviamo a calcolare il prodotto scalare standard della seguente coppia di vettori.

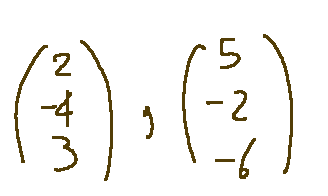
image.png

In questo caso identifichiamo subito come calcolare il prodotto scalare tra questi due vettori che chiameremo V e W.
Quindi i due vettori saranno:
v = (v1,v2,v3)
w = (w1,w2,w3)
Il prodotto scalare si calcola nella seguente maniera:

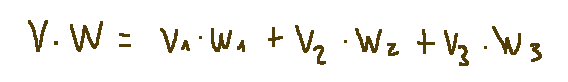
image.png

Ricordiamo come sono i vettori v e w

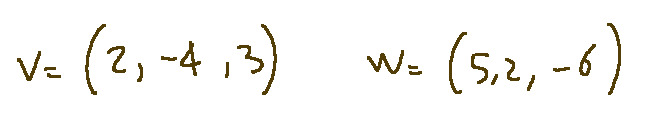
image.png

Procediamo ora con il calcolo andando a sostituire i valori nella prima formula mostrata in questo esercizio

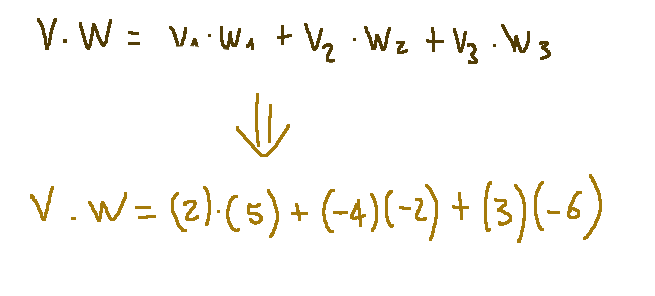
image.png

Proseguendo con i calcoli arriveremo a questo risultato

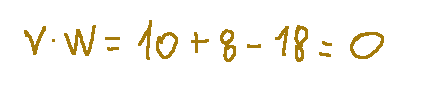
image.png

Il prodotto scalare sarà quindi

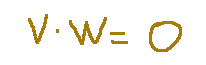
image.png

In questo caso possiamo dire che i vettori sono ortogonali

Esempio 2
Troviamo ora il prodotto scalare standard delle seguenti coppie di vettori. (1 3 0 -1) e (0 2 -1 4)

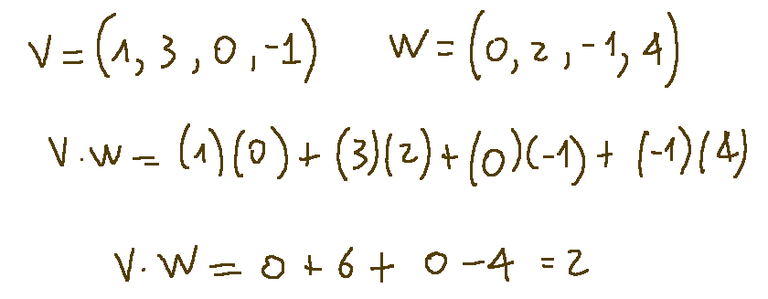
image.png
Il prodotto scalare è il seguente

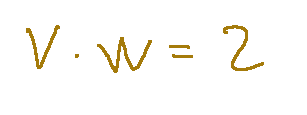
image.png

Conclusioni
Il prodotto scalare tra due vettori in uno scalare (un numero) è alla base di molte altre operazioni matematiche.

Domanda
Avete mai provato a fare il prodotto scalare tra due vettori?

THE END

geometry learn proofofbrain ctp palnet stem archon pimp vyb
0
0
0.000
11 comments
avatar

Its an interesting lesson. Mathematical calculations involving scalar products are always intriguing and it's a vast and complex area of maths and physics. Thanks for writing and happy Sunday.

0
0
0.000
Reply
avatar

Scalar product is the most difficult topic you have ever thought us
It’s quite hard to

0
0
0.000
Reply
avatar

You are building up little interest into me for calculations. Maybe I should start of practicing for fun 🥰

0
0
0.000
Reply
avatar

Congratulations @stefano.massari! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)

You have been a buzzy bee and published a post every day of the week.

You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word STOP

0
0
0.000
Reply