22-11-2024 - Analytic Geometry - Affine Subspaces [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
22-11-2024 - Analytic Geometry - Affine Subspaces [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_70)

Affine Subspaces
Description
Affine subspaces generalize the notions of line and plane in space. They can also be thought of as a generalization of vector subspaces.
We can also state the following.
In analytic geometry, affine subspaces are generalizations of vector subspaces, obtained by "translating" a vector subspace into a larger space. They are sets of points that maintain the linear structure of a vector subspace but do not necessarily contain the origin.

Formal definition
An affine subspace of a vector space

is a set of points defined as follows:

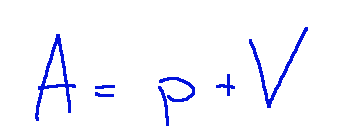
Where:
p belongs to Rn is a fixed point called base point or reference point
V is a subset of Rn and is a vector subspace
We can say that A is the set of all points of the form

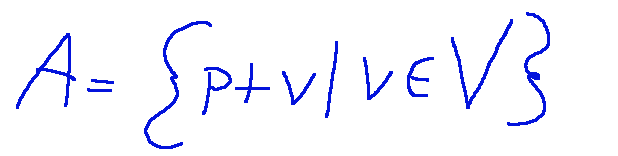
This means that A is a translated copy of V with the base point p that moves the vector subspace V away from the origin.

Properties
-Dimension: The dimension of an affine subspace A is the same as the dimension of the subspace V
-Translation: An affine subspace does not necessarily contain the origin, unless the base point p is the origin itself.
-Cartesian equations: An affine subspace can also be described by a system of linear equations,
Example
Let's now try to find an affine line and plane.
Consider p and V as follows:

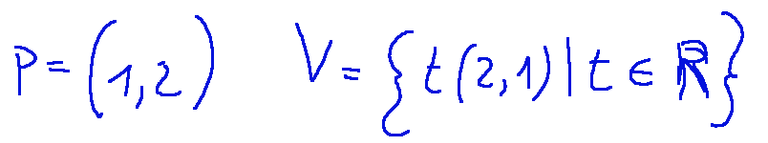
The affine line is the set of points

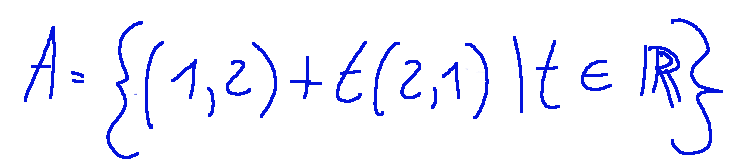
Graphically it is a line that passes through the point (1,2) and has a direction parallel to the vector (2,1)

Affine Plane
Let's consider p = (1,0,0) and V the plane generated by the vectors (1,0,1) and (0,1,1)
The affine plane is the set

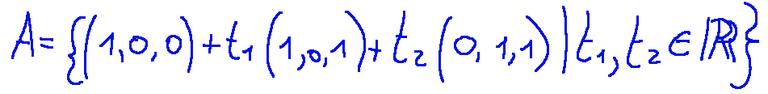
Conclusions
The difference between affine subspaces and vector subspaces is that vector subspaces always contain the origin (0), while affine subspaces do not necessarily contain the origin, unless the point p is the origin itself.
An affine subspace is essentially a "shifted copy" of a vector subspace.

Question
Have you studied affine subspaces and vector subspaces in analytic geometry or linear algebra?

---

---

[ITALIAN]
22-11-2024 - Geometria analitica - Sottospazi affini [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_70)

Sottospazi affini
Descrizione
I sottospazi affini generalizzano le nozioni di retta e piano nello spazio. Essi possono essere pensati anche come una generalizzazione dei sottospazi vettoriali.
Possiamo anche affermare quanto segue.
In geometria analitica, i sottospazi affini sono generalizzazioni dei sottospazi vettoriali, ottenuti "traslando" un sottospazio vettoriale in uno spazio più grande. Sono insiemi di punti che mantengono la struttura lineare di un sottospazio vettoriale ma non devono necessariamente contenere l'origine.

Definizione formale
Un sottospazio affine di uno spazio vettoriale

è un insieme di punti definito come segue:

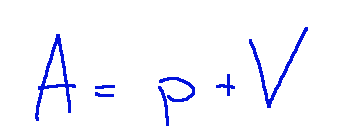
Dove:
p appartiene a Rn è un punto fissato chiamato punto base o punto di riferimento
V è un sottoinsieme di Rn ed è un sottospazio vettoriale
Possiamo dire che A è l’insieme di tutti i punti della forma

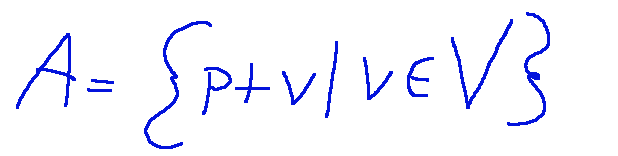
Questo significa che A è una copia traslata di V con il punto base p che sposta il sottospazio vettoriale V lontano dall’origine.

Proprietà
-Dimensione: La dimensione di un sottospazio affine A coincide con la dimensione del sottospazio V
-Traslazione: Un sottospazio affine non contiene necessariamente l’origine, a meno che il punto base p sia l’origine stessa.
-Equazioni cartesiane: Un sottospazio affine può essere descritto anche da un sistema di equazioni lineari,
Esempio
Proviamo ora a trovare una retta e un piano affine.
Consideriamo p e V come segue:

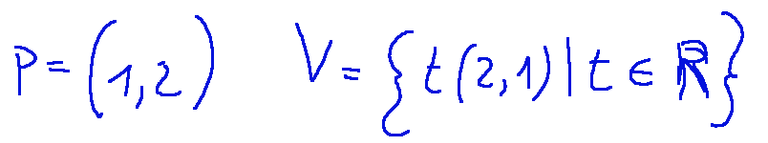
La retta affine è l’insieme di punti

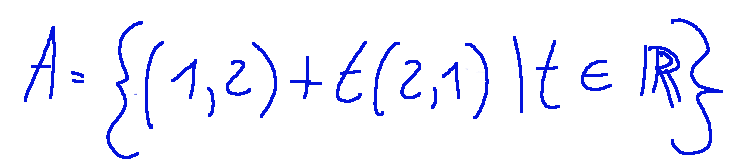
Graficamente è una retta che passa per il punto (1,2) e ha direzione parallela al vettore (2,1)

Piano affine
Consideriamo p = (1,0,0) e V il piano generato dai vettori (1,0,1) e (0,1,1)
Il piano affine è l’insieme

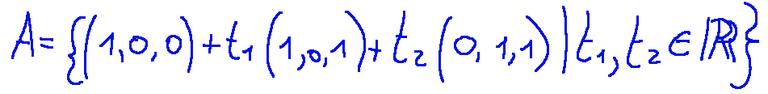
Conclusioni
La differenza tra sottospazi affini e sottospazi vettoriali è che i sottospazi vettoriali contengono sempre l’origine (0), mentre i sottospazi affini non contengono necessariamente l’origine, a meno che il punto p sia l’origine stessa.
Un sottospazio affine è sostanzialmente una "copia spostata" di un sottospazio vettoriale.

Domanda
Avete studiato in geometria analitica o in algebra lineare sottospazi affini e sottospazi vettoriali?

THE END