22-06-2024 - Energy systems - Pelton turbine (2) [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
22-06-2024 - Energy systems - Pelton turbine (2) [EN]-[IT]

Pelton turbine (2)

Speed ​​Triangles
Below is a diagram of a Pelton turbine blade with speed triangles

Below, the velocity triangle diagram is reported in a more explanatory manner

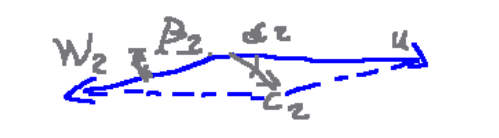
The reduction coefficient
The speed reduction coefficient at the distributor of a Pelton turbine is the ratio between c1 and c1id.
The formula is shown below.

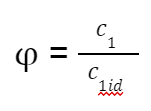
Where:
c1 = jet speed
c1id = ideal jet speed

In other words we can say that the speed reduction coefficient at the distributor is defined as the ratio between the actual speed of the water at the exit of the distributor and the theoretical speed that the water would have without losses.
This coefficient is used to understand how efficient the distributor is in converting potential energy into kinetic energy.

The relative speed reduction coefficient
The relative speed reduction coefficient of a Pelton turbine depends on the fluid dynamic losses in the impeller.
Its formula is shown below:

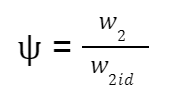
The relative speed reduction coefficient is fundamental for optimizing the performance of Pelton turbines.
Its importance impacts the following three topics:
-Efficiency
-Design
-Performance analysis

Conclusions
The speed reduction coefficient at the distributor and the relative speed reduction coefficient of a Pelton turbine indicate the efficiency of the turbine itself.

Request
Have you ever heard of the 1800s American inventor Lester Allan Pelton?

---

---

ITALIAN
22-06-2024 - Sistemi energetici - Turbina Pelton (2)[EN]-[IT]

Turbina Pelton (2)

Triangoli delle velocità
Qui di seguito è schematizzata una pala di una turbina Pelton con i triangoli delle velocità

Qui si seguito lo schema del triangolo delle velocità è riportato in maniera più esplicativa

Il coefficiente di riduzione
Il coefficiente di riduzione della velocità al distributore di una turbina Pelton è il rapporto tra c1 e c1id.
Qui di seguito è rappresentata la formula.

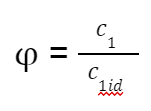
Dove:
c1 = velocità del getto
c1id = velocità ideale del getto

In altre parole possiamo dire che Il coefficiente di riduzione della velocità al distributore è definito come il rapporto tra la velocità effettiva dell'acqua all'uscita del distributore e la velocità teorica che l'acqua avrebbe senza perdite.
Questo coefficiente viene usato per capire quanto sia efficiente il distributore nel convertire l’energia potenziale in energia cinetica.

Il coefficiente di riduzione della velocità relativa
Il coefficiente di riduzione della velocità relativa di una turbina Pelton dipendente dalle perdite fluidodinamiche nella girante.
Qui di seguito è mostrata la sua formula:

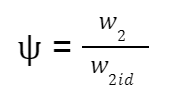
Il coefficiente di riduzione della velocità relativa è fondamentale per l’ottimizzazione delle prestazioni delle turbine Pelton.
La sua importanza impatta sui seguenti tre argomenti:
-Efficienza
-Progettazione
-Analisi delle prestazioni

Conclusioni
Il coefficiente di riduzione della velocità al distributore ed il coefficiente di riduzione della velocità relativa di una turbina Pelton indicano l'efficienza della turbina stessa.

Domanda
Avete mai sentito parlare dell'inventore statunitense del 1800 Lester Allan Pelton?

THE END