19-10-2024 - Linear Algebra - Linearly Independent Column Vectors [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
19-10-2024 - Linear Algebra - Linearly Independent Column Vectors [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_092)

linearly independent column vectors
Column vectors are a rather important concept of linear algebra and are also part of analytical geometry.
Note: We can express vectors in two ways, row vectors and column vectors.
example of a row vector, when a matrix A is formed by a single row

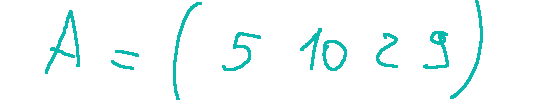
example of a column vector, when a matrix A is formed by a single column

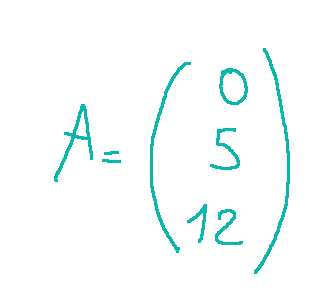
In the case of the row vector the matrix is ​​of order (1 x n) and in the case of the row vector expressed above the matrix A has order (1 x 4)
In the case of the column vector the matrix is ​​of order (m x 1) that in the case shown before the matrix A has order (3 x 1)

Brief note on the column vector
A column vector is a vector written in vertical form, that is a matrix with only one column. For example a column vector in a three-dimensional space R3 is written in the following way.

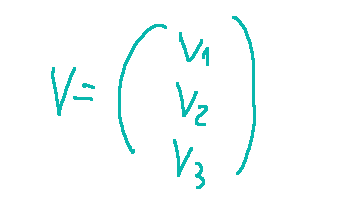
linearly independent column vectors
Linearly independent column vectors are a fundamental concept in linear algebra and concern the idea of ​​linear independence between vectors.
The Concept
Linear independence of a set of column vectors is a concept that expresses when these vectors cannot be expressed as a linear combination of the other vectors in the group.
Algebraic definition
A set of vectors

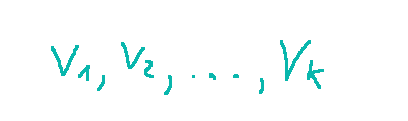
is linearly independent if the only solution to the following equation:

and when all coefficients c1,c2,..., ck are equal to zero, that is

linearly dependent vectors
If instead there exists a combination of coefficients not all equal to zero that satisfies this equation, the vectors are linearly dependent, that is, at least one of them can be written as a linear combination of the others.

PS: In the next article I will try to give some concrete examples to clarify the concept.

Conclusions
Given a set of vectors it is possible to study whether they are linearly dependent or independent of each other.

Question
Did you study linearly independent vectors at school?

[ITALIAN]
19-10-2024 - Algebra lineare - vettori colonna linearmente indipendenti [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_092)

vettori colonna linearmente indipendenti
I vettori colonna sono un concetto dell'algebra lineare piuttosto importanti e fanno parte anche della geometria analitica.
Nota: I vettori possiamo esprimerli in due modi, vettori riga e vettori colonna.
esempio di un vettore riga, quando una matrice A è formata da una sola riga

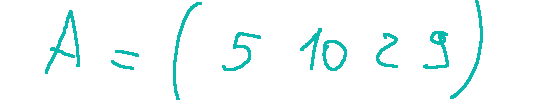
esempio di un vettore colonna, quando una matrice A è formata da una sola colonna

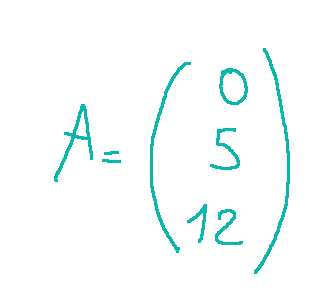
Nel caso del vettore riga la matrice è di ordine (1 x n) e nel caso del vettore riga espresso sopra la matrice A ha ordine (1 x 4)
Nel caso del vettore colonna la matrice è di ordine (m x 1) che nel caso mostrato prima la matrice A ha ordine (3 x 1)

Breve nota sul vettore colonna
Un vettore colonna è un vettore scritto in forma verticale, cioè una matrice con una sola colonna. Ad esempio un vettore colonna in uno spazio tridimensionale R3 è scritto nella seguente maniera.

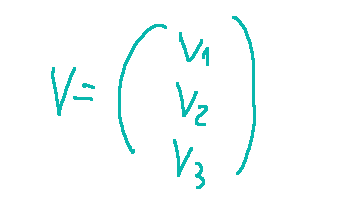
vettori colonna linearmente indipendenti
I vettori colonna linearmente indipendenti sono un concetto fondamentale in algebra lineare e riguardano l'idea di indipendenza lineare tra vettori.
Il concetto
L'indipendenza lineare di un insieme di vettori colonna è un concetto che esprime quando questi vettori non possono essere espressi come combinazione lineare degli altri vettori del gruppo.
Definizione algebrica
Un insieme di vettori

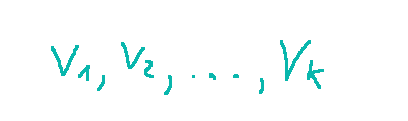
è linearmente indipendente se l'unica soluzione alla seguente equazione:

e quando tutti i coefficienti c1,c2,..., ck sono uguali a zero, cioè

vettori linearmente dipendenti
Se invece esiste una combinazione di coefficienti non tutti uguali a zero che soddisfa questa equazione, i vettori sono linearmente dipendenti, cioè almeno uno di essi può essere scritto come combinazione lineare degli altri.

PS: Nel prossimo articolo proverò a fare degli esempi concreti per chiarire il concetto.

Conclusioni
Dato un insieme di vettori è possibile studiare se sono linearmente dipendenti o indipendenti tra di loro.

Domanda
Avete studiato a scuola i vettori linearmente indipendenti?

THE END