19-06-2024 - Energy systems - Operation - peripheral speed[EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
19-06-2024 - Energy systems - Operation - peripheral speed[EN]-[IT]
Exercise - peripheral speed
Let's consider we have a centrifugal pump and try to find the peripheral speed at the impeller exit and the radial component of the absolute speed corresponding to the volume flow rate of water disposed of.
Below are the data:
A centrifugal pump is characterized by an impeller with a diameter D=200 mm, axial width of the blades hp=18mm at the outlet.
The blades are inclined backwards with an angle β=25°.
The pump processes a volumetric flow rate of water equal to Q=8dm3/s at a rotation speed of 12 rpm
Below is the table which shows the data in a schematic manner:

Below is what we will try to calculate in the hypothesis of stationary operation of the pump and one-dimensional flow:

Procedure
-1-
Calculation of u2, i.e. calculation of the peripheral speed at the impeller exit.
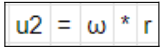
Below is the development of the formula

Result

-2-
Calculation of cr2, i.e. the radial component of the absolute velocity corresponding to the volume flow rate of water disposed of.
We know that the flow rate can be calculated in the following way:
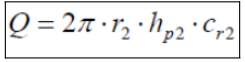
From which we can obtain Cr2 in the following way:
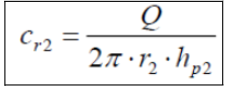
From which we will obtain the following operations:

Result

Conclusions
To calculate the peripheral speed of a pump impeller we need to know the diameter, while to calculate the radial component of the absolute speed corresponding to the volume flow rate of water disposed of we need to know the flow rate data.
Request
Are these types of calculations complex or somewhat understandable to you? Have you ever done similar exercises at school?

ITALIAN
19-06-2024 - Sistemi energetici - Esercizio - velocità periferica[EN]-[IT]
Esercizio - velocità periferica
Consideriamo di avere una pompa centrifuga e cerchiamo di trovare la velocità periferica all’uscita della girante e la componente radiale della velocità assoluta corrispondente alla portata in volume di acqua smaltita.
Qui di seguito i dati:
Una pompa centrifuga è caratterizzata da una girante di diametro D=200 mm larghezza assiale delle pale hp=18mm in uscita.
Le pale sono inclinate all’indietro con un angolo β=25°.
La pompa elabora una portata volumetrica d’acqua pari a Q=8dm3/s al regime di rotazione di 12 giri/s
Qui di seguito la tabella che riporta i dati in maniera schematica:

Qui di seguito quello che cercheremo di calcolare nell'ipotesi di funzionamento stazionario della pompa e di flusso monodimensionale:

Svolgimento
-1-
Calcolo di u2, cioè calcolo della velocità periferica all’uscita della girante.
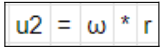
Qui di seguito lo sviluppo della formula

Risultato

-2-
Calcolo di cr2, ovvero la componente radiale della velocità assoluta corrispondente alla portata in volume di acqua smaltita.
Sappiamo che la portata si può calcolare nella seguente maniera:
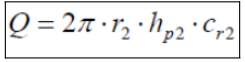
Da cui ci possiamo ricavare Cr2 nel seguente modo:
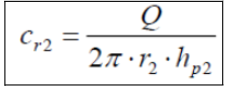
Da cui ricaveremo le seguenti operazioni:

Risultato

Conclusioni
Per calcolare la velocità periferica di una girante di una pompa abbiamo bisogno di conoscere il diametro, mentre per calcolare la componente radiale della velocità assoluta corrispondente alla portata in volume di acqua smaltita abbiamo bisogno di conoscere il dato della portata.
Domanda
Questa tipologia di calcoli vi risultano complessi o piuttosto comprensibili? Avete mai eseguito esercizi simili a scuola?
THE END
Honestly, it looks like a complex calculation to me
I appreciate you for this subject though
Love it!
Energy system is quite needed to understand how things really work
So proud to have a smart friend on Hive. It seems like a complex plus complicated topic !LOLZ , but I really appreciate the effort put into explaining it. Understanding energy systems is definitely important for understanding how things function. Thanks for this good friend
lolztoken.com
The bartender shouts Geto out of my pub! We don’t serve your type!
Credit: ifiwasfrank
@stefano.massari, I sent you an $LOLZ on behalf of theringmaster
(2/2)