12-10-2024 - Analytic geometry - linear combinations [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
12-10-2024 - Analytic geometry - linear combinations [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_094)
linear combinations
Linear combinations are the simplest expression that we can write in a vector space.
Usually the expression of the linear combination is formed by geometric vectors with coefficients. The writing looks like this

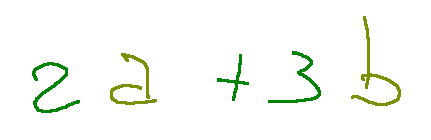
Where:
a and b are the geometric vectors
2 and 3 are the coefficients

example
Let's write a linear combination of the vectors w and v shown below.

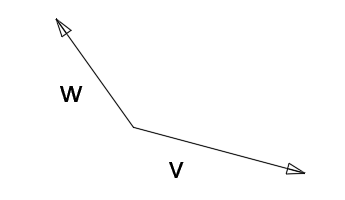
Linear combination
Let's consider the following linear combination

2 w + 3 v

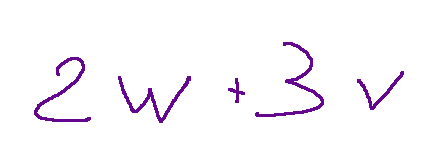
We will get the following result.

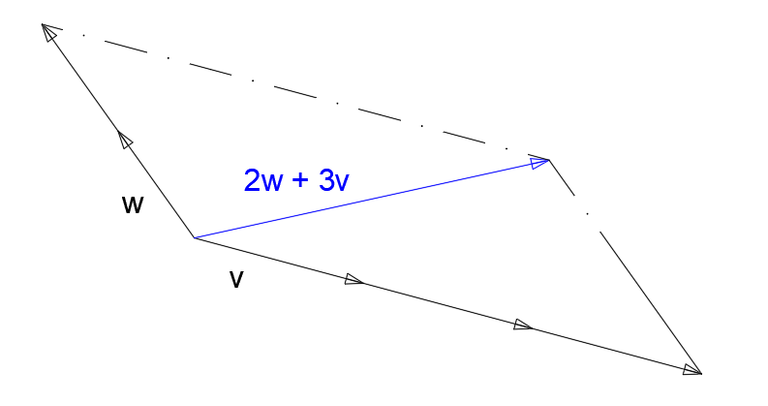
Linear combination of column vectors
Column vectors can also have linear combinations.
Consider the following column vectors.

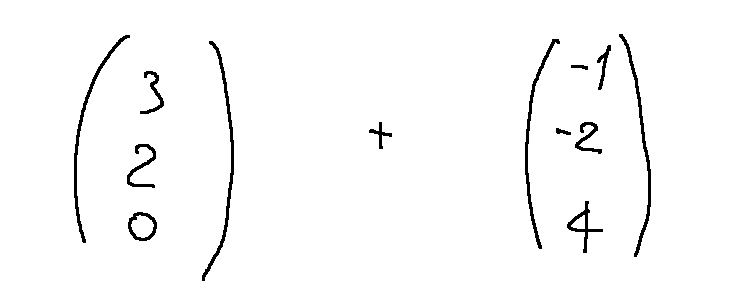
We use the coefficients 2 and -1. Below is the writing of the linear combination between column vectors.

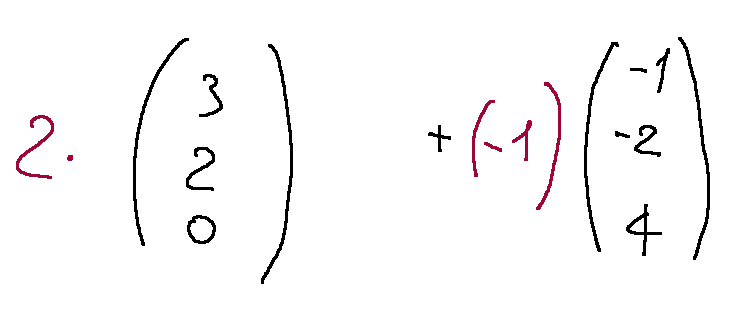
Below in blue is the result

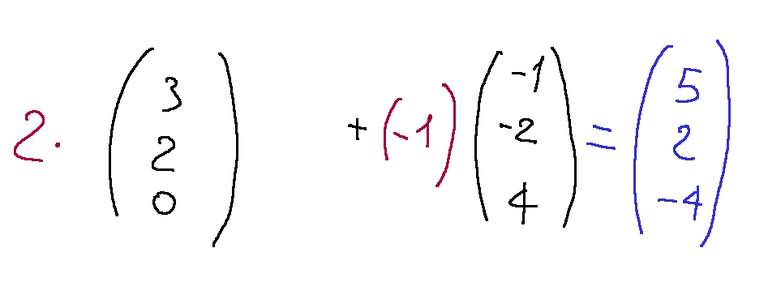
Conclusions
Linear combinations can be performed either on vectors with scalar or on column and coefficient vectors.

Question
Have you ever done these studies in your geometry or algebra classes?

---

---

[ITALIAN]
12-10-2024 - Geometria analitica - combinazioni lineari [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_094)
combinazioni lineari
Le combinazioni lineari sono la più semplice espressione che possiamo scrivere in uno spazio vettoriale.
Solitamente l'espressione della combinazione lineare è formata da vettori geometrici con coefficienti. La scrittura è simile alla seguente

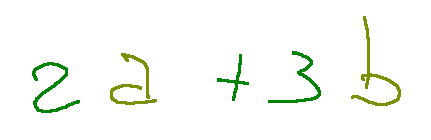
Dove:
a e b sono i vettori geometrici
2 e 3 sono i coefficienti

esempio
Scriviamo una combinazione lineare dei vettori w e v mostrati qui di seguito.

Combinazione lineare
Prendiamo in considerazione la combinazione lineare seguente

2 w + 3 v

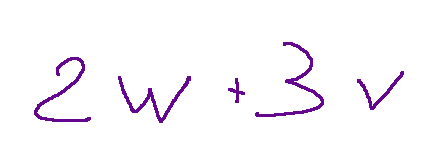
Otterremo il seguente risultato.

Combinazione lineare dei vettori colonna
Anche i vettori colonna possono avere combinazioni lineari.
Consideriamo i seguenti vettori colonna.

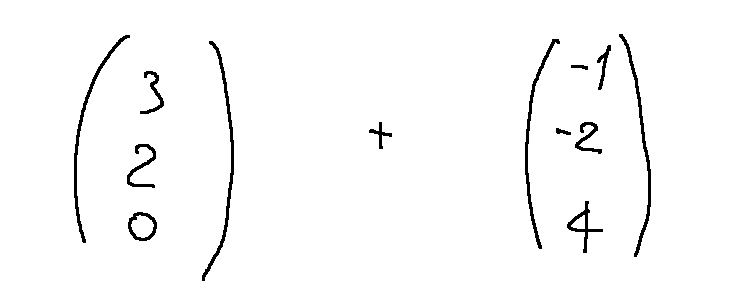
Usiamo i coefficienti 2 e -1. Qui di seguito è riportata la scrittura della combinazione lineare tra vettori colonna.

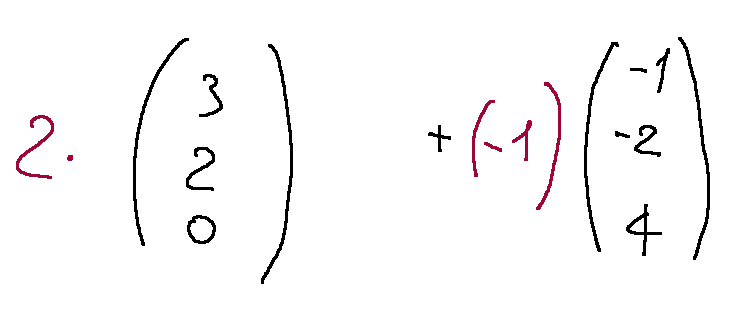
Qui di seguito in blu è riportato il risultato

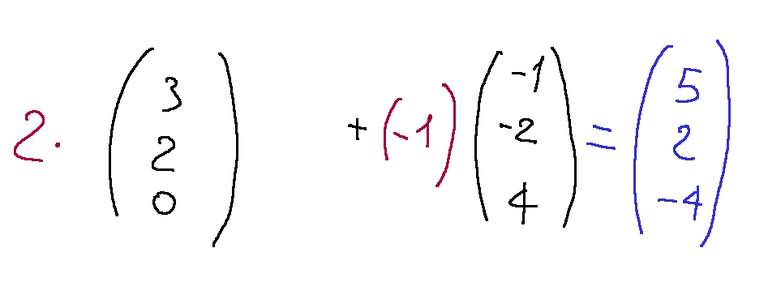
Conclusioni
Combinazioni lineari si possono effettuare sia su vettori con scalare oppure con vettori colonna e coefficiente.

Domanda
Avete mai eseguito questi studi durante le vostre lezioni di geometria o di algebra?

THE END