09-10-2024 - Analytical Geometry - Operations [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
09-10-2024 - Analytical Geometry - Operations[EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_096)
Operations

associative property
In the operations between sets that can be done in analytical geometry, the concept of associative property is often used. A concept that is also very well known in algebra.
The associative property expresses the way in which the terms of an operation can be grouped and is said to be present if the result is not altered after having made changes in form that we will see later. It applies to the operations of addition and multiplication.
Associative sum
Associative sum exists when for every trio of real numbers a, b and c the following rule holds:

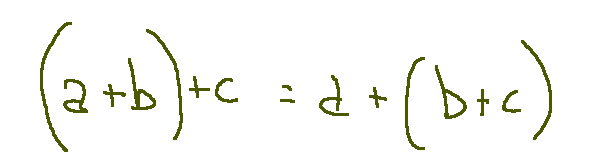
Associative multiplication
Associative multiplication exists when for every trio of real numbers a, b and c the following rule holds: rule:

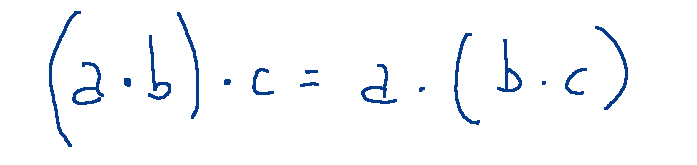
Commutative Property
The commutative property concerns the order of elements on which an operation is performed. It applies to addition and multiplication operations.
Commutative sum

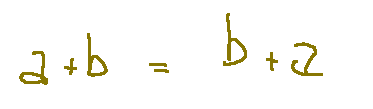
Commutative multiplication

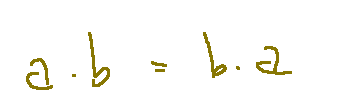
Associative property of addition on C

Let's try to prove the associative property of addition on C.
Remember that C is the set of complex numbers. Complex numbers are the largest set of numbers of all because they contain natural, integer, rational, real and complex numbers.

Let's consider addition and write the associative property

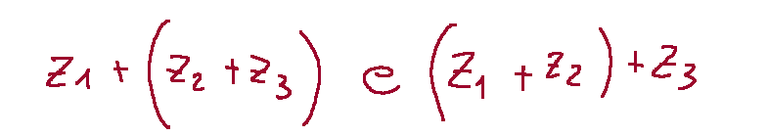
Remember: C (set of complex numbers)
For each z1,z2,z3 belonging to C (writing zi = ai + ibi for i = 1; 2; 3) prove that they are equal

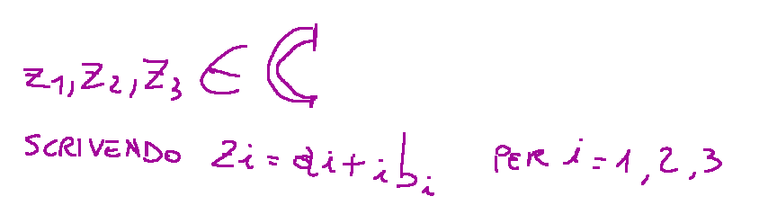
Basically, exchanging the addends or factors does not change the result

commutative property of multiplication on C
Let's try to demonstrate the commutative property of multiplication on C.
If we thought of explicitly calculating z1z2 and z2z1 for each z1; z2 belonging to C (set of complex numbers) we will note that the result of z1z2 will be equal to that of z2z1
So the following is verified:

Conclusions
The associative property and the commutative property are the most well-known properties of algebraic sets.

Question
Do you remember if you studied the associative property and the commutative property at school?

[ITALIAN]
09-10-2024 - Geometria analitica- Operazioni[EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_096)
Operazioni

proprietà associativa
Nelle operazioni tra insiemi che si possono fare in geometria analitica si usa spesso il concetto di proprietà associativa. Un concetto che è molto conosciuto anche in algebra.
La proprietà associativa esprime il modo in cui si possono raggruppare i termini di un'operazione e si dice che è presente se il risultato non viene alterato dopo aver effettuato dei cambi di forma che vedremo in seguito. Si applica alle operazioni di somma e moltiplicazione.
Somma associativa
La somma associativa esiste quando per ogni trio di numeri reali a,b e c vale la seguente regola:

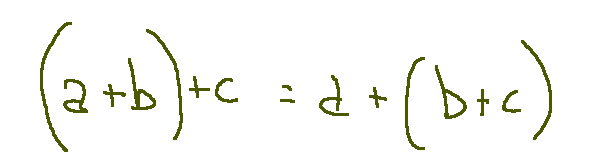
Moltiplicazione associativa
La moltiplicazione associativa esiste quando per ogni trio di numeri reali a,b e c vale la seguente regola:

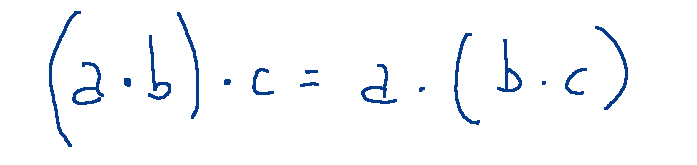
Proprietà commutativa
La proprietà commutativa riguarda l'ordine degli elementi su cui si esegue un'operazione. Essa si applica alle operazioni di somma e moltiplicazione.
Somma commutativa

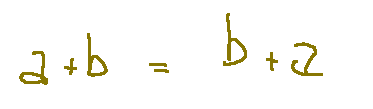
Moltiplicazione commutativa

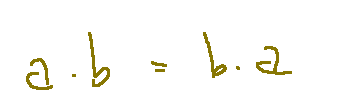
Proprietà associativa dell’addizione su C

Proviamo a dimostrare la proprietà associativa dell’addizione su C.
Si ricorda che C è l’insieme dei numeri complessi. I numeri complessi sono l'insieme di numeri più vasto di tutti in quanto sono contenuti al suo interno i numeri naturali, interi, razionali, reali e complessi.

Prendiamo in considerazione l’addizione e scriviamo la proprietà associativa

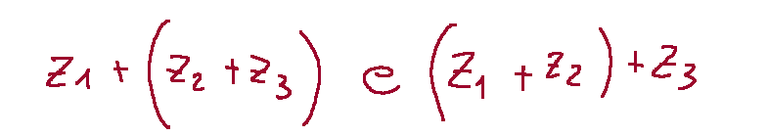
Ricordiamo: C (insieme dei numeri complessi)
Per ogni z1,z2,z3 appartenente a C (scrivendo zi = ai + ibi per i = 1; 2; 3) dimostra che essi sono uguali

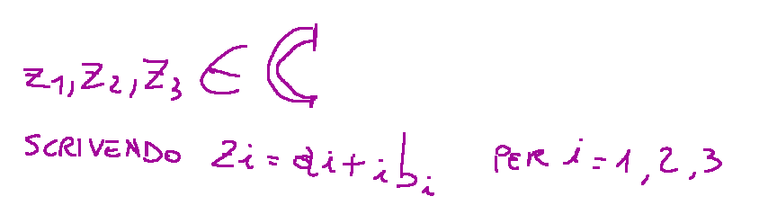
Sostanzialmente scambiando gli addendi o i fattori il risultato non cambia

proprietà commutativa della moltiplicazione su C
Proviamo a dimostrare la proprietà commutativa della moltiplicazione su C.
Se pensassimo di calcolare esplicitamente z1z2 e z2z1 per ogni z1; z2 appartenenti a C (insieme dei numeri complessi) noteremo che il risultato di z1z2 sarà uguale a quello di z2z1
Quindi è verificato quanto segue:

Conclusioni
La proprietà associativa e la proprietà commutativa sono le proprietà più conosciute degli insiemi algebrici.

Domanda
Vi ricordate se a scuola avete studiato la proprietà associativa e quella commutativa?

THE END