08-06-2024 - Energy systems - Adimensionalization of quantities[EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
08-06-2024 - Energy systems - Adimensionalization of quantities[EN]-[IT]

Adimensionalization of quantities

Variables
The variables by which incompressible fluid turbomachines can be described are the following:
-Impeller diameter, D [m]
-Volume flow rate, Q [m3/s]
-Angular velocity of the impeller, ω [rad/s]
-Fluid density, ρ [kg/m3]
-Dynamic viscosity, μ [Pa/s]
-Hydraulic efficiency, η
-Specific work, g*H [J/kg]
-Power, P [W]
So we have 8 variables.

While the fundamental quantities to describe an incompressible fluid turbomachine are length, mass and time. So we have 3 fundamental quantities.
So as system variables we will choose diameter, speed and density. Below is the detailed description.
-Impeller diameter, D [m]
-Angular velocity of the impeller, ω [rad/s]
-Fluid density, ρ [kg/m3]

Buckingham's theorem
Buckingham's theorem states that given a physical process described by n physical variables, it is possible to use n-k parameters in dimensionless form, where k is the number of dimensionally independent quantities.
So let's think about the n-k relationship and we will therefore have n - k = 8-3=5

Example with the volumetric flow rate Q (m3/s):

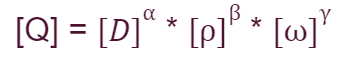
We can rewrite this relationship from the fundamental quantities

Now it is possible to obtain a system of three equations with three unknowns

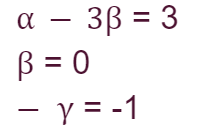
From here we can obtain the following values: α=3, β=0 and γ=1.

So we can say that the dimensionless value of the flow rate is the following:

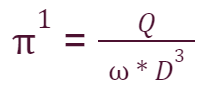
In this case π1 is also called flow coefficient.

Independent variables
In a turbomachine the dimensions of the machine, the properties of the
fluid and operating conditions are considered as independent variables.

The link between dependent and independent dimensionless groups for incompressible fluid turbomachinery
The most used dimensionless groups for calculations carried out on turbomachines are:
-Reynolds number
-Nusselt number
-Dimensionless volumetric flow number
-Dimensionless power number

These dimensionless groups are related to each other and the functional form describing these relationships can be expressed as:

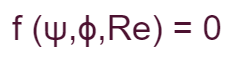
Example
Suppose we have a turbomachine and we want to predict the behavior based on experimental data. We could have a graph representing the Nusselt Number as a function of the dimensionless volumetric flow Number for different values ​​of the Reynolds Number.
Once the data is collected, it can be used to design the turbomachinery in final operating conditions.

Fluid dynamics similarity
The fluid dynamic analysis of a project has the aim of determining the forces exerted by the fluid on the system under consideration. The mathematical equations to be solved are extremely complex even in the simplest cases, so this has been felt since
immediately the need to have empirical methods to overcome the obstacle.

To try to understand the behavior of a turbomachine you could create a prototype, but this is an expensive solution.
The most immediate way is to create a small-scale model.
Consider two models whose axes of symmetry are parallel. Two models have a geometric similarity relationship if it is possible to establish a biunivocity between their points such that two points (P1,Q1) are chosen on the first model
and (P2,Q2) on the second, the ratio between the quantities is a constant, called the geometric similarity ratio, having
expression:

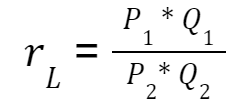
At this point it is possible to establish a kinematic relationship between the two models.

Conclusions
The fluid dynamic similarities allow the creation of relatively low-cost calculation models and then have useful data for the design of the final version of a turbomachine.

Request
Did you study Nusselt Number or Reynolds Number in school? Have you already heard of these dimensionless quantities?

---

---

ITALIAN
08-06-2024 - Sistemi energetici - Adimensionalizzazione delle grandezze[EN]-[IT]

Adimensionalizzazione delle grandezze

Variabili
Le variabili mediante le quali possono essere descritte le turbomacchine a fluido incomprimibile sono le seguenti:
-Diametro della girante, D [m]
-Portata volumetrica, Q [m3/s]
-Velocità angolare della girante, ω [rad/s]
-Densità del fluido, ρ [kg/m3]
-Viscosità dinamica, μ [Pa/s]
-Rendimento idraulico, η
-Lavoro specifico, g*H [J/kg]
-Potenza, P [W]
Quindi abbiamo 8 variabili.

Mentre le grandezze fondamentali per descrivere una turbomacchina a fluido incomprimibile sono la lunghezza, la massa ed il tempo. Quindi abbiamo 3 grandezze fondamentali.
Quindi come variabili del sistema sceglieremo diametro, velocità e densità. Qui di seguito riporto la descrizione dettagliata.
-Diametro della girante, D [m]
-Velocità angolare della girante, ω [rad/s]
-Densità del fluido, ρ [kg/m3]

Il teorema di Buckingham
Il teorema di Buckingham afferma che dato un processo fisico descritto da n variabili fisiche, è possibile utilizzare n-k parametri in forma adimensionale, dove k è il numero di grandezze dimensionalmente indipendenti.
Quindi pensiamo alla relazione n-k e avremo quindi n - k = 8-3=5

Esempio con la portata volumetrica Q (m3/s):

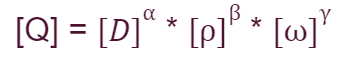
Possiamo riscrivere questa relazione dalle grandezze fondamentali

Ora è possibile ottenere un sistema di tre equazioni con tre incognite

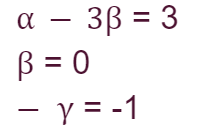
Da qui possiamo ricavare i seguenti valori: α=3, β=0 e γ=1.

Quindi possiamo dire che il valore adimensionalizzato della portata è il seguente:

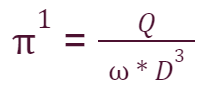
In questo caso π1 è detto anche coefficiente di portata.

Variabili indipendenti
In una turbomacchina le dimensioni della macchina, le proprietà del
fluido e le condizioni operative sono considerate come variabili indipendenti.

Il legame fra i gruppi adimensionali dipendenti e quelli indipendenti per le turbomacchine a fluido incomprimibile
I gruppi adimensionali più usati per i calcoli effettuati sulle turbomacchine sono:
-Numero di Reynolds
-Numero di Nusselt
-Numero di flusso volumetrico adimensionale
-Numero di potenza adimensionale

Questi gruppi adimensionali sono correlati tra loro e la forma funzionale che descrive queste relazioni può essere espressa come:

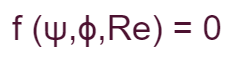
Esempio
Supponiamo di avere una turbomacchina e vogliamo prevedere il comportamento in base ai dati sperimentali. Potremmo avere un grafico che rappresenta il Numero di Nusselt in funzione del Numero di flusso volumetrico adimensionale per diversi valori del Numero di Reynolds.
Una volta raccolti i dati, questi possono essere usati per progettare la turbomacchina in condizioni operative definitive.

Similitudine fluidodinamica
L’analisi fluidodinamica di un progetto ha lo scopo di determinare le forze esercitate dal fluido sul sistema preso in esame. Le equazioni matematiche da risolvere sono estremamente complesse anche nei casi più semplici, quindi si è avvertita fin
da subito l’esigenza di disporre di metodi empirici per poter superare l’ostacolo.

Per cercare di comprendere il comportamente di una turbomacchina si potrebbe creare un prototipo, ma questa è una soluzione costosa.
La strada più immediata è la realizzazione di un modello in scala ridotta.
Si considerino due modelli i cui assi di simmetria siano paralleli. Due modelli sono in rapporto di similitudine geometrica se è possibile stabilire fra i loro punti una biunivocità tale che comunque si scelgano due punti (P1,Q1) sul primo modello
e (P2,Q2) sul secondo, il rapporto fra le grandezze è una costante, detta rapporto di similitudine geometrica, avente
espressione:

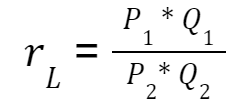
A questo punto è possibile stabilire una relazione di tipo cinematico tra i due modelli.

Conclusioni
Le similitudini fluidodinamiche permettono di realizzare dei modelli di calcolo dai costi relativamente contenuti per poi avere dei dati utili alla progettazione della versione definitiva di una turbomacchina.

Domanda
Avete studiato a scuola il Numero di Nusselt o il Numero di Reynolds? Avete già sentito nominare queste grandezze adimensionali?

THE END