06-06-2024 - Energy systems - Dimensional analysis

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
06-06-2024 - Energy systems - Dimensional analysis [EN]-[IT]

Dimensional analysis

What is it for
Dimensional analysis allows you to address the studies of fluid dynamic phenomena by applying the adimensionalization technique.
In many real cases which concern the study of phenomena relating to conduction (but not only), the number of dimensional variables is considerable and, consequently, the mathematical solution is very complex: dimensionless grouping the variables, thus decreasing the number of independent ones. This simplifies the mathematical aspect and also the presentation of the results.

Advantages
Dimensional analysis brings advantages in various studies applied to the world of physics. Below are the advantages that can be drawn from dimensional analysis in the study of turbomachinery.
-Reduction in the number of experimental tests that would serve to understand the relationships between the various quantities.
-Estimation of the performance of a prototype through tests carried out on a similar model.
-You can understand the type of machine most suitable for particular conditions of head, speed and flow rate.

Buckingham's theorem
Edgar Buckingham was an American physicist, mathematician and chemist who left his theorem to mathematics. He was born in 1867 and died in 1940.
Buckingham's theorem is also known as the Pi theorem theorem.
This theorem states that given a physical process described by an equation, even undefined in its analytical form, in which n physical variables appear, if the fundamental quantities of these n variables are k, then the problem can be expressed as a function of n-k dimensionless groups .
Descriptive example
If the analysis in question depends on five quantities which, in turn, have as a unit of measurement a certain combination of the three fundamental quantities of the international system, then the analysis can describe the problem with a function f of two dimensionless groups P1 and P2.

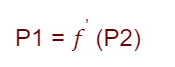
We can describe it another way.
This theorem basically states that a physical process described by n physical variables can use n-k parameters in dimensionless form, where k is the number of dimensionally independent quantities.
Its mathematical translation would be as follows:
given a function of n variables:

We can express this function in terms of n-k dimensionless parameters

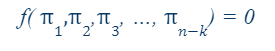
NOTE: Each parameter represents a combination of linearly independent variables.

Dimensionless groups
We can describe the procedure for determining dimensionless groups starting from an important concept.
Each dimensional quantity P can be expressed through a combination of the fundamental quantities. Below is the sentence expressed as a formula:

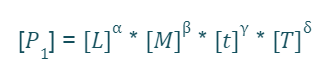
Where:
L = length (m)
M = mass (kg)
t = time (s)
T = temperature (K)

The second step is to determine the dimensionless groups. To do this, a maximum number k of linearly independent variables P1, P2,... Pk must be selected from the n variables.

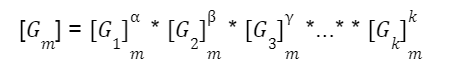
Finally, having reached this point, the n-k dimensionless groups can be obtained as follows.

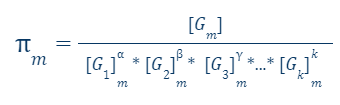
Conclusions
Dimensionlessization can be done in different ways, depending on the reference quantities that are chosen for each variable. This mathematical process serves to make the relationships between physical quantities more understandable and to build less complicated formulas.

Request
Have you already heard of dimensionlessness? Have you by any chance addressed this topic at school? I consider dimensionality to be a complex topic, is this the case for you too?

---

---

ITALIAN
06-06-2024 - Sistemi energetici - Analisi dimensionale [EN]-[IT]

Analisi dimensionale

A cosa serve
L’analisi dimensionale consente di affrontare gli studi dei fenomeni fluidodinamici applicando la tecnica della adimensionalizzazione.
In molti casi reali che riguardano lo studio dei fenomeni relativi alla conduzione (ma non solo), il numero delle variabili dimensionali è notevole e, di conseguenza, la soluzione matematica è molto complessa: l’adimensionalizzazione raggruppa le variabili, diminuendo così il numero di quelle indipendenti. Ciò semplifica l’aspetto matematico e anche la presentazione dei risultati.

Vantaggi
L’analisi dimensionale porta dei vantaggi in diversi studi applicati al mondo della fisica. Qui di seguito i vantaggi che si possono trarre dall’analisi dimensionale nello studio delle turbomacchine.
-Riduzione del numero di prove sperimentali che servirebbero a comprendere le relazioni tra le varie grandezze.
-Stima delle prestazioni di un prototipo tramite dei test effettuati su un modello simile.
-Si può capire il tipo di macchina più adatto per particolari condizioni di prevalenza, velocità e portata.

Il teorema di Buckingham
Edgar Buckingham è stato un fisico, matematico e chimico statunitense che ha lasciato alla matematica il suo teorema. Nasce nel 1867 e muore nel 1940.
Il teorema di Buckingham è noto anche come il teorema teorema Pi greco.
Questo teorema afferma che dato un processo fisico descritto da un'equazione anche indefinita nella sua forma analitica, nella quale compaiano n variabili fisiche, se le grandezze fondamentali di queste n variabili sono k, allora il problema può essere espresso in funzione di n-k gruppi adimensionali.
Esempio descrittivo
Se l’analisi in esame dipende da cinque grandezze le quali, a loro volta, hanno come unità di misura una certa combinazione delle tre grandezze fondamentali del sistema internazionale, allora l’analisi può descrivere il problema con una funzione f di due gruppi adimensionali P1 e P2.

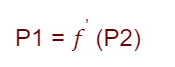
Possiamo descriverlo in un'altra maniera.
Questo teorema fondamentalmente afferma che un processo fisico descritto da n variabili fisiche, è possibile utilizzare n-k parametri in forma adimensionale, dove k è il numero di grandezze dimensionalmente indipendenti.
La sua traduzione matematica sarebbe la seguente:
data una funzione di n variabili:

Possiamo esprimere questa funzione in termini di n-k parametri adimensionali

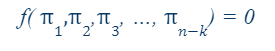
NOTA: Ogni parametro rappresenta una combinazione delle variabili linearmente indipendenti.

Gruppi adimensionali
Possiamo descrivere la procedura per la determinazione dei gruppi adimensionali partendo da un concetto importante.
Ogni grandezza dimensionale P può essere espressa tramite una combinazione tra le grandezze fondamentali. Qui di seguito la frase espressa come formula:

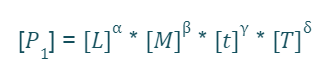
Dove:
L = lunghezza (m)
M = massa (kg)
t = tempo (s)
T = temperatura (K)

Il secondo passaggio è quello di determinare i gruppi adimensionali. Per fare questo si devono selezionare fra le n variabili un numero massimo k di variabili linearmente indipendenti P1, P2,... Pk.

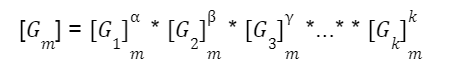
Infine, arrivati a questo punto, si possono ricavare gli n-k gruppi adimensionali come segue.

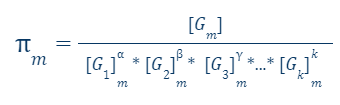
Conclusioni
L'adimensionalizzazione può essere fatta in diversi modi, a secondo delle grandezze di riferimento che si scelgono per ogni variabile. Questo processo matematico serve per rendere più comprensibili le relazioni tre le grandezze fisiche e costruire formule meno complicate.

Domanda
Avete già sentito parlare di adimensionalizzazione? Per caso a scuola avete affrontato questo argomento? Io ritengo l'adimensionalizzazione un argomento complesso, è così anche per voi?

THE END