05-10-2024 - Analytical geometry - Requirements [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
05-10-2024 - Analytical geometry - Requirements [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_098)
Requirements
Analytical geometry is a branch of mathematics that combines geometry and algebra. It basically allows you to analyze points, lines, curves and other geometric figures using algebraic equations.
For this reason, that is, because in this branch there are algebraic elements, it is important to have some basic notions.
In this article I would not like to address topics related to analytical geometry itself, but to the requirements that you need to have before starting to study or move within analytical geometry.
Below are some requirements.

Sets
Here is the graphic representation to indicate that an object x belongs to a set I

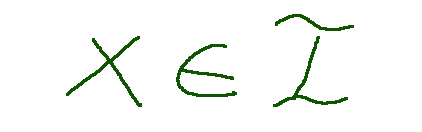
Here is the graphic representation to indicate that an object x does not belong to a set I

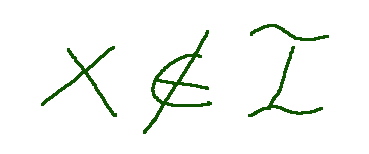
Here is the graphic representation to indicate the number of the elements of a set.

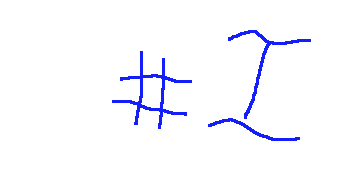
If the set has no elements, the graphical representation is as follows.

Note:
A set I is said to be finite if it has a finite number of elements. Here is how it is indicated.

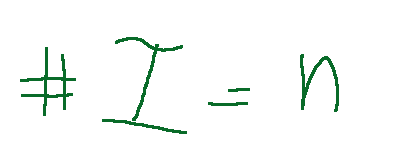
A set I is said to be infinite if it has an infinite number of elements. Here is how to indicate.

Subsets
In analytic geometry, a subset is simply a set of points that belong to a larger set
Given a set I, a set J is called a subset of I if every
element that belongs to J also belongs to I. This is indicated in the following manner:

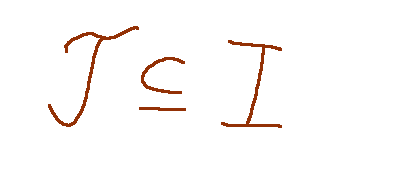
or

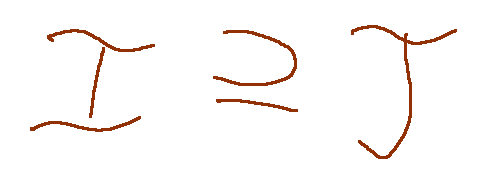
Note: Two sets I1 and I2 coincide if and only if they are subsets of each other.

Intersection and union
In analytical geometry, the intersection of two sets refers to the set of points that belong to both sets. The intersection is represented by the symbol ∩.
So if there are two sets, one is set A and the other is set B, their intersection is represented as follows.

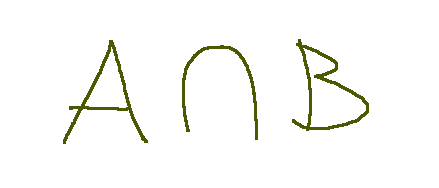
Conclusions
To understand analytical geometry it is essential to have some basics as a requirement, otherwise understanding will be very difficult from the beginning.

Question
Have you heard of analytical geometry before or is this your first time?

[ITALIAN]
05-10-2024 - Geometria analitica- Requisiti [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_098)
Requisiti
La geometrica analitica è un ramo della matematica che unisce la geometria e l'algebra. Sostanzialmente consente di analizzare punti, linee, curve e altre figure geometriche utilizzando equazioni algebriche.
Per questo motivo, cioè per il motivo che in questo ramo ci sono degli elementi algebrici, è importante avere delle nozioni di base.
In questo articolo non vorrei affrontare argomenti relativi proprio alla geometria analitica, ma ai requisiti che bisogna avere prima di iniziare a studiare o a muoversi dentro la geometria analitica.
Qui di seguito alcuni requisiti.

Insiemi
Questo di seguito la rappresentazione grafica per indicare che un oggetto x appartiene ad un insieme I

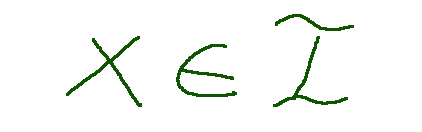
Questo di seguito la rappresentazione grafica per indicare che un oggetto x non appartiene ad un insieme I

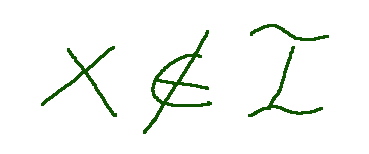
Questo di seguito la rappresentazione grafica per indicare il numero degli elementi di un insieme.

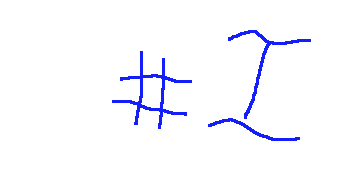
Se l'insieme non ha elementi la rappresentazione grafica è la seguente.

Nota:
Un insieme I è detto finito se ha un numero finito di elementi. Qui di seguito come si indica.

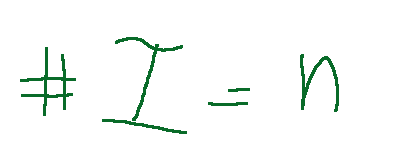
Un insieme I è detto infinito se ha un numero infinito di elementi. Qui di seguito come si indica.

Sottoinsiemi
In geometria analitica, un sottoinsieme è semplicemente un insieme di punti che appartengono a un insieme più ampio
Dato un insieme I, un insieme J è detto sottoinsieme di I se ogni
elemento che appartiene a J appartiene anche a I. Questo si indica nella seguente maniera:

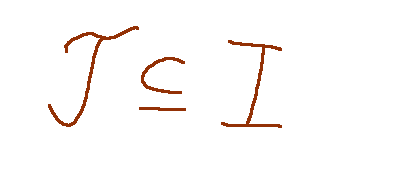
oppure

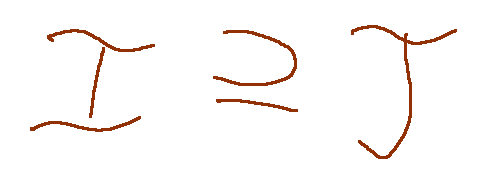
Nota: Due insiemi I1 e I2 coincidono se e solo se sono l’uno sottoinsieme dell’altro.

Intersezione e unione
In geometria analitica, l'intersezione di due insiemi si riferisce all'insieme dei punti che appartengono ad entrambi gli insiemi. L'intersezione è rappresentata con il simbolo ∩.
Quindi se ci sono due insiemi, uno è l'insieme A e l'altro è l'insieme B, la loro intersezione si rappresenta come segue.

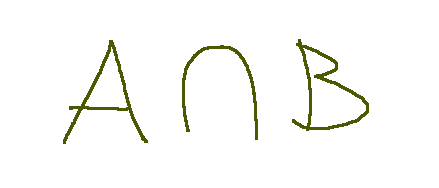
Conclusioni
Per comprendere la geometria analitica è fondamentale avere alcune basi come requisito, altrimenti la comprensione risulterà sin dall'inizio molto difficile.

Domanda
Avete già sentito parlare di geometria analitica oppure è la prima volta?

THE END