03-06-2024 - Energy systems - work equation [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
03-06-2024 - Energy systems - work equation [EN]-[IT]

Brief notes
Recall that the work of a constant force in a rectilinear displacement is the dot product between the force and displacement vectors.
The work of a constant force is calculated in the following way:
L=F s cos(α)
Where:
L = work
F = strength
s = displacement

Reference
To explain in a general way what the equation of work with differences in kinetic energy is, let's try to think of an impeller.

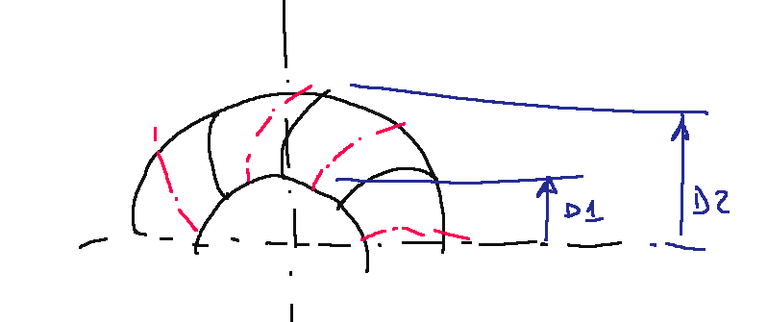
Vector relation
Taking the impeller shown above as an example we can deduce the following vector relationship.

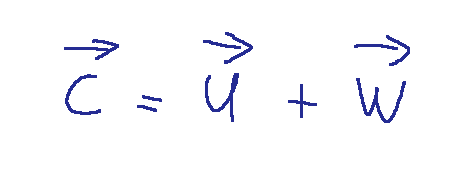
Where:
c = the absolute velocity of the fluid
u = the driving speed of the impeller, equal to ωR
w = the relative velocity of the fluid

From the formula we deduce that the absolute speed of the fluid is the sum of the driving speed of the impeller and the relative speed of the fluid. So the absolute velocity is given by two contributions.

Work equation
To deduce the work equation for kinetic energy differences in finite form we need to:
-think of an observer who is in a fixed point

• think of a mobile observer for which the contribution of the centrifugal force following the rotation of the impeller must also be added
  -Consider for the mobile observer the principle of conservation of mechanical energy
  -Transform the result obtained by substituting the first equation obtained when thinking about the fixed observer and integrating it.
  At this point we will have
  The kinetic energy difference work equation in finite form

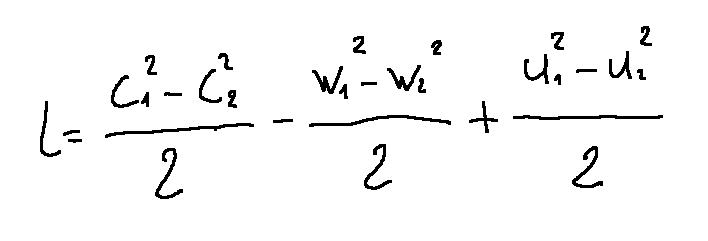
conservation equation
The conservation equation of energy in mechanical form in differential terms for a system integral with the impeller is the following.

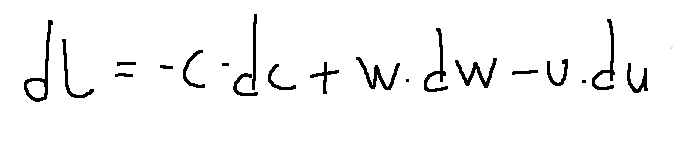
energy equation in thermodynamic form
If we try to think about the energy equation in thermodynamic form, we know that moving to the moving reference system does not involve
variations in heat exchanged or enthalpy.
In this case we will therefore have the following formula

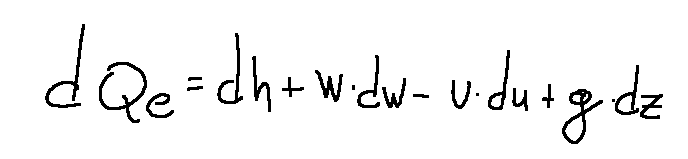
reaction degree Χ of the turbomachine
In an impeller (see drawing shown at the beginning of the article) the exchanged work can be defined by two contributions
-Work per share (L az)
-Work per reaction (L reaction)
The degree of reaction X of a turbomachine is the following ratio:

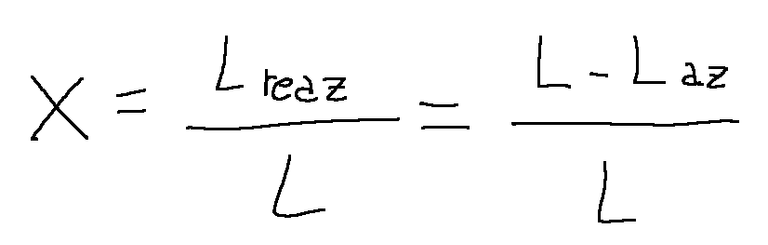
Reaction Machines Definition
On the basis of the formula expressed above, those machines that have Χ=0 are defined as action machines, while those that have reaction are defined as reaction machines
so Χ>0.

Important Considerations
Action machines have no pressure variation between the inlet and outlet of the impeller, while in reaction machines the contribution is positive.

Conclusions
Machines that have a degree of reaction Χ of the turbomachine = 0 are called action machines, while those for which Χ>0 are called reaction machines.

Request
Have you ever studied a jet car? Or have you ever used turbines at work?

ITALIAN
03-06-2024 - Sistemi energetici - equazione del lavoro [EN]-[IT]

Brevi cenni
Ricordiamo che ll lavoro di una forza costante in uno spostamento rettilineo è il prodotto scalare tra i vettori forza e spostamento.
Il lavro di una forza costante si calcola nella seguente maniera:
L=F·s·cos(α)
Dove:
L = lavoro
F = forza
s = spostamento

Riferimento
Per spiegare in maniera generale cosa sia l'equazione del lavoro alle differenze di energia cinetica proviamo a pensare ad una girante.

Relazione vettoriale
Prendendo come esempio la girante mostrata prima possiamo dedurre la seguente relazione vettoriale.

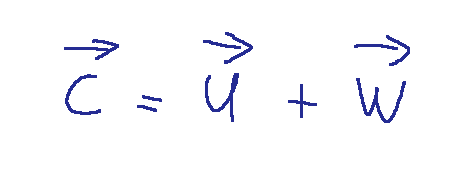
Dove:
c = la velocità assoluta del fluido
u = la velocità di trascinamento della girante, pari a ωR
w = la velocità relativa del fluido

Dalla formula deduciamo che la velocità assoluta del fluido è la somma della velocità di trascinamento della girante e la velocità relativa del fluido. Quindi la velocità assoluta è data da due contributi.

Equazione del lavoro
Per dedurre l'equazione del lavoro alle differenze di energia cinetica in forma finita bisogna:
-pensare ad un osservatore che si trova in un punto fisso
-pensare ad un osservatore mobile per cui occorre aggiungere anche il contributo della forza centrifuga a seguito della rotazione della girante
-Considerare per l'osservatore mobile il principio di conservazione dell'energia meccanica
-Trasformare il risultato ottenuto fino sostituendo la prima equazione ottenuta nel pensare all'osservatore fisso ed integrandola.
A questo punto avremo
L'equazione del lavoro alle differenze di energia cinetica in forma finita

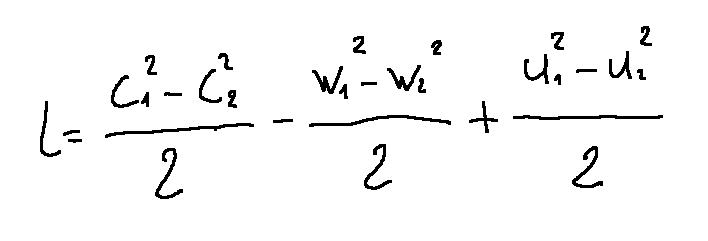
equazione di conservazione
L'equazione di conservazione dell'energia in forma meccanica in termini differenziali per un sistema solidale con la girante è la seguente.

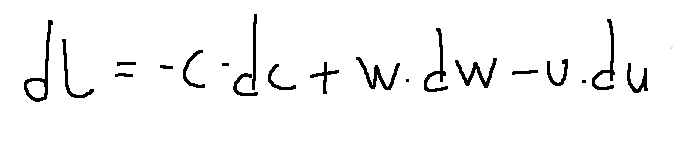
equazione dell'energia in forma termodinamica
Se proviamo a pensare all’equazione dell’energia in forma termodinamica, sappiamo che passare al sistema di riferimento mobile non comporta
variazioni di calore scambiato, né di entalpia.
In questo caso avremo quindi la seguente formula

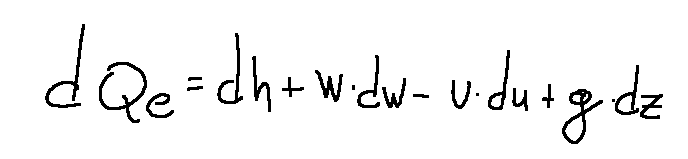
grado di reazione Χ della turbomacchina
In una girante (vedi disegno mostrato all'inizio dell'articolo) il lavoro scambiato può essere definito tramite due contributi
-Lavoro per azione (L az)
-Lavoro per reazione (L reaz)
Il grado di reazione X di una turbomacchina è il seguente rapporto:

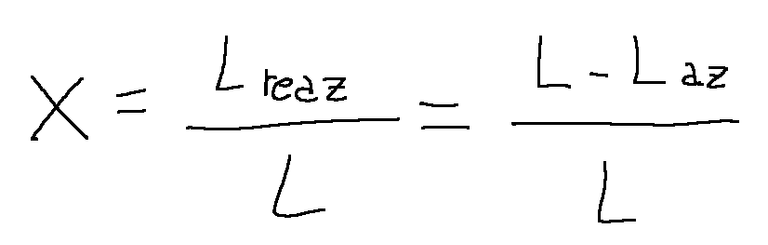
Definizione delle macchine a reazione
In base alla formula espressa prima si definiscono ad azione le macchine che hanno Χ=0, si definiscono a reazione quelle
per cui Χ>0.

Considerazioni importanti
Le machine ad azione non hanno variazione di pressione tra ingresso ed uscita della girante, mentre nelle macchine motrici a reazione il contributo è positivo.

Conclusioni
Le macchine che hanno un grado di reazione Χ della turbomacchina = 0 vengono chiamate macchine ad azione , quelle invece per cui per cui Χ>0 vengono chiamate macchine a reazione.

Domanda
Avete mai studiato una macchina a reazione? Oppure avete mai usato delle turbine sul lavoro?

THE END