02-06-2024 - Energy systems - The energy conservation equation in mechanical form [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
02-06-2024 - Energy systems - The energy conservation equation in mechanical form [EN]-[IT]

Brief notes
Let's start from the concept that mechanical energy is the sum of kinetic energy and potential energy, usually indicated with the letter E.
Its formula can be expressed as follows:
E=K+U
Reasoning on the formula just expressed it can be deduced that in the presence of only conservative forces the principle of conservation of energy applies

The principle of conservation of mechanical energy is often abbreviated as the principle of conservation of energy.
This establishes that in an isolated system in which only conservative forces act, mechanical energy is conserved.

Example system
Below is an image of a system that can be taken as an example.

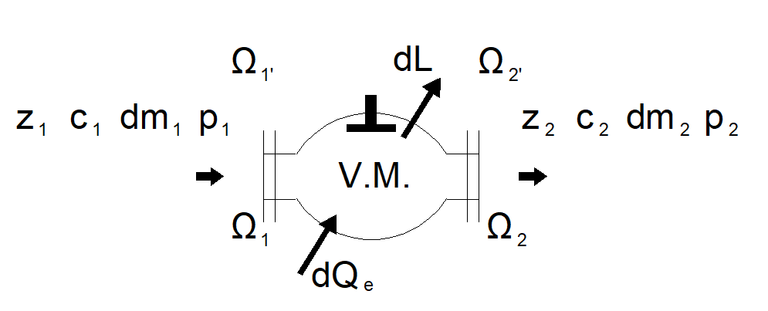
In this case we consider a system made up of the fluid enclosed between the sections Ω1 and Ω2 at time t0, at time t0+dt the same mass will be enclosed between the sections Ω1' and Ω2' (see previous figure)

In this case we will have a job that could come as a contribution deriving from external forces. Below is a list of work that can come from outside:
-The work of gravitational forces
-The mechanical work exchanged with the mobile organ
-The work of moving in the entry and exit sections
-The work of the friction forces (since the flow is one-dimensional it will be limited to the walls of the ducts)

From everything we have said we can arrive at the following formula. the formula expressed below is considered very important not only within the study of energy systems, but also in thermodynamics and fluid dynamics.

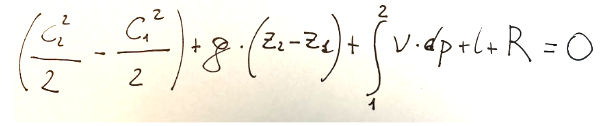
The above expression is also known as the Bernoulli equation and is generalized for steady, one-dimensional flow.

Below is the same formula but expressed in differential terms.

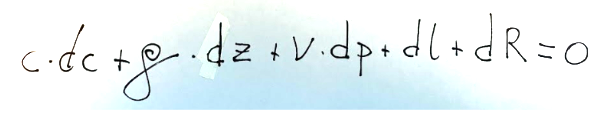
Conclusions
The conservation equation of energy in mechanical form corresponds to the Bernoulli equation.

Request
Have you ever heard of the Swiss mathematician and physicist Bernoulli? Do you remember if you studied any of his formulas or theorems at school?

---

---

ITALIAN
02-06-2024 - Sistemi energetici - L’equazione di conservazione dell’energia in forma meccanica [EN]-[IT]

Brevi cenni
Partiamo dal concetto che l'energia meccanica è la somma dell'energia cinetica e dell'energia potenziale, solitamente indicata con la lettera E.
La sua formula può essere espressa come segue:
E=K+U
Ragionando sulla formula appena espressa si può dedurre che in presenza di sole forze conservative vale il principio di conservazione dell'energia

Il principio di conservazione dell'energia meccanica spesso viene abbreviato come il principio di conservazione dell'energia.
Questo stabilisce che in un sistema isolato in cui agiscono solo forze conservative l'energia meccanica si conserva.

Sistema d'esempio
Qui di seguito è riportata un'immagine di un sistema che può essere preso come esempio.

In questo caso consideriamo un sistema costituito dal fluido racchiuso tra le sezioni Ω1 e Ω2 al tempo t0, al tempo t0+dt la stessa massa sarà racchiusa tra le sezioni Ω1’ e Ω2’ (vedi figura precedente)

In questo caso avremo un lavoro che potrebbe arrivare come apporto derivante dalle forse esterne. Qui di seguito un elenco del lavoro che può giungere dall'esterno:
-Il lavoro delle forze gravitazioni
-Il lavoro meccanico scambiato con l'organo mobile
-Il lavoro di spostamento nelle sezioni di ingresso e di uscita
-Il lavoro delle forze do attrito (essendo il flusso unidimensionale esso sarà limitato alle pareti dei condotti)

Da tutto ciò che abbiamo detto possiamo arrivare alla seguente formula. la formula qui di seguito espressa è ritenuta molto importante non solo all'interno dello studio dei sistemi energetici, ma anche in termodinamica ed in fluidodinamica.

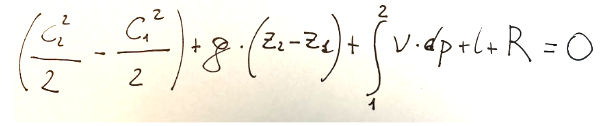
L'espressione qui sopra riportata è conosciuta anche come equazione di Bernoulli ed è generalizzata per flusso stazionario e unidimensionale.

Qui di seguito la stessa formula però espressa in termini differenziali.

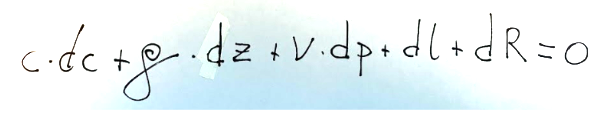
Conclusioni
L’equazione di conservazione dell’energia in forma meccanica corrisponde all'equazione di Bernoulli.

Domanda
Avete mai sentito parlare del matematico e fisico svizzero Bernoulli? Ricordate se a scuola avete studiato qualche sua formula o teorema?

THE END