Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|

Greetings to everyone! In my last blog, we were discussing about commutator relations. I hope we understood what commutation of operator is and we have also discussed some short-cut method also. (This will help you to save time). Today, we shall see some other properties in commutation, do some problems based on what we learnt just to refresh the memory and then on we will start a very important topic i.e., Eigen value and eigen function. These two things are so important in quantum mechanics. We will study them and as always see some of their properties as well.

Let us see some of the other commutator properties. So far we have studied commutator of two operators, but what if there are three? what if two of them are in a additive manner or what about commutation of an operator with a constant?

See there? in equations 5 and 6, the constant (k) had no effect on the commutation. It just got multiplied with the commutation of operator A and B. The constant does not vary with respect to the operators. We study whether two variables can be calculated at the same time or not ( commutation being =0 or ≠0). Since the constant has no effect on it, we can just bring it out of its shell from the commutative bracket.

Similarly in equation 7, since a constant does not vary, so we can definitely calculate the value of operator  and constant at the same time. There is no confusion. So, it becomes 0 (we have already studied commutation =0 and ≠0 cases)

Now, in equation 8, if we can calculate an operator A then we can definitely calculate function of that operator at the same time. For more clarification, if we can calculate position x̂, then definitely we an also calculate x̂² at the same time.

Problem) What will be the commutation of the following involving position and momentum operators?

Solution

Just to let you know, ℏ is called reduced Planck's constant or Dirac's constant and it's value is h/2π, where h is Planck's constant.

Problem) The commutator of the kinetic energy operator T̂_x and the momentum operator p̂_x will be?

Solution

Since commutation of two same quantities is always 0.

Problem) When the operator -ℏ d²/dx² operates on the function e^-ikx, the result is?

Solution

Problem) The linear momentum of a particle described by the wave function e^-ikx is?

Solution

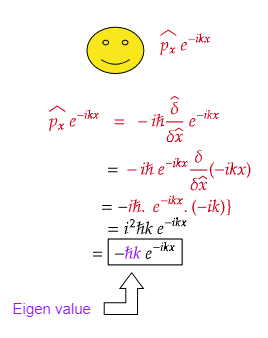
We actually found the same wave function i.e., e^-ikx at the end of the operation. The constant value -ℏk is called a eigen value here. We shall see now what a eigen function and eigen value actually is!

Eigenvalue and Eigenfunction

Eigenvalue equations are those equations in which on operating a function, we get the same function again only multiplied by a constant value. The constant value is called eigenvalue and the function is called eigenfunction.

Suppose that the effect of operating on some function f(x) with the linear operator  is simply to multiply f(x) by a certain constant k. We then say that f(x) is an eigenfunction of  with eigen value k. Eigen is a German word meaning characteristic. As part of the definition , we shall require that the eigen function f(x) is not identically zero. By this we mean that, although f(x) may vanish at various points, it is not everywhere zero.

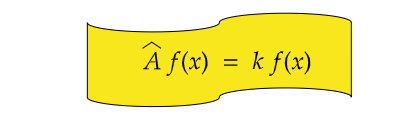
An example is, e^2x is an eigenfunction of the operator d/dx with eigenvalue 2.

(d/dx) e^2x = 2 e^2x

However, sin2x is not an eigenfunction of d/dx since, (d/dx)(sin2x) = 2 cos2x, which is not a constant times sin2x.

Properties

• If a function is multiplied by a contant, then it will not affect the eigen value.

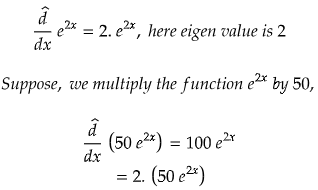
Here, 100 is not the eigenvalue which you might think! The simple reason for it is that now, the function is not e^2x rather it is 50 e^2x. So, we have to have the same function at the end. So the eigen value again becomes 2, i.e., not affected by multiplying the function by a constant.

• If the operator is multiplied by some constant, it will affect/change eigenvalue.

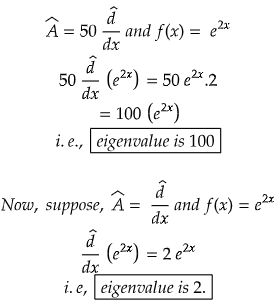
It is clearly shown in the above example that if the operator is multiplied by some constant, eigenvalue changes.

What we learnt?

• We studied some commutator properties apart from the operator ones. Studied cases involving constants within commutator relations.

• Applied commutator properties to solve problems

• Studied basics to eigenvalue and eigenfunction. Discussed two of the important properties that has impact whether the eigen value will change or remain unchanged.

Software used:

The mathematical equations are prepared using mathcha.io editor.

---

Read My Previous Blogs:

---

How to find Expression of an Operator and Commutation Relations |ChemFam #76|

Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|

Exploring Total Differentials and Cyclic Rules as Mathematical Maestros in Thermodynamics |ChemFam #74|

A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|

A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|

Decoding Liver Function Tests through Chemistry |ChemFam #71|

Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|

Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|

Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|

The Silent Revolution: How Polymers are Shaping Our World? |ChemFam #67|

Beyond the Bin: The Many Faces of Plastic Management |ChemFam #66|

Spectrophotometry Simplified: The Beer-Lambert Law in Spectrophotometry |ChemFam #65|

Chromatography: Unraveling the Science of Separation |ChemFam #64|

Colorful Clues: The Magical World of Chemical Indicators |ChemFam #63|

Colloids in Action: Impacting Your Daily Life More Than You Think |ChemFam #62|

The Complex Landscape of Opioid Analgesics: Addressing The Concerns |ChemFam #61|

Genetic Engineering: Pioneering Progress or Ethical Predicament? |ChemFam #60|

The Guardians Against Microbial Menace: Antibacterial Agents |ChemFam #59|

The Cholesterol Conundrum: The Story of Statins |ChemFam #58|

Unveiling The Control Of Chemistry: How Hormones Dictate Our Mood |ChemFam #57|

Thermodynamic Versus Kinetic Control of Reactions |ChemFam #56|

Bosons: The Quantum Glue That Holds The Universe Together |ChemFam #55|

PS The thumbnail image is being created by me using canva.com

---

Thanks for stopping by :)