Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|

Greetings to everyone! In my previous post, we have studied specifically about eigenfunctions and eigenvalues. The eigenequations are very important in quantum mechanics as we are going to see them frequently. So, hope you do some problems related to it. Today, we shall briefly study the wave-particle duality of electron, particularly the famous de-Broglie equation. Then we shall talk and discuss about some postulates of quantum mechanics. Here, we shall study an important property called normalization of wavefunction.

In 1905, Einstein suggested that light has a dual character; as wave and also as particle. Louis de Broglie, a French physicist proposed that matter also has a dual character; as wave and as particle. The name wavicle was suggested for such particle. Contradicting the theory provided by Bohr in which Bohr treated electron as a particle; de Broglie's theory suggested matter and therefore, electron also, has a dual character, both as material particle and as a wave. He derived an expression for calculating the wave length λ of a particle of mass m moving with velocity v according to which,^{(Puri, Sharma and Pathania, 47th edition, Principles of Physical Chemistry, Wave mechanical treatment of simple systems, 33p)}

Here, p is linear momentum of the particle and h is Planck's constant. From doing few mathematical changes, we can have a relation between kinetic energy, KE and wavelength, λ and from energy equation from classical mechnics involving Boltzman constant, k_B, we get a different euation.

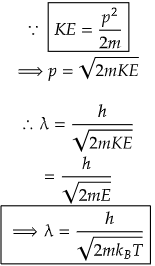
As electric potential, v is the amount of work done, w in moving a unit charge, q from infinity to a point. So, we have, w=qv, unit in joules. Unit of energy? Joules right? So, we can also have,

This wave-particle duality is a central concept in quantum mechanics and is a key element in the development of the wave function, which describes the probability distribution of finding a particle in a particular state.

The de Broglie equation is particularly important when dealing with small particles, such as electrons, whose behaviors are more accurately described by quantum mechanics rather than classical mechanics. In experiments involving particles at the atomic and subatomic levels, the de Broglie wavelength is a crucial parameter in understanding phenomena like diffraction and interference, which are characteristic of wave behavior.

Postulates of Quantum Mechanics

• (1) The physical state of a system at time t is described by a wavefunction Ψ(x,t)
• (2) Ψ and its derivatives must be (i) finite, (ii) single valued and (iii) continuous.

• (3) An acceptable wavefunction is that which gives 100% information regarding the system, i.e., the wavefunction must be normalized. The normalization condition ensures that the probability of finding a particle in any possible location is equal to 1.

Mathematically, the normalization condition for a one-dimensional wavefunction Ψ(r) is given by:

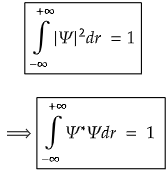
Where, Ψ^* is the complex conjugate of Ψ formed by replacing i with -i whenever it occurs in the function Ψ (i=√(−1))

This condition ensures that the total probability of finding the particle within the entire spatial domain is unity. Here,∣Ψ∣² represents the probability density function, and integrating it over all possible positions guarantees that the particle is somewhere in space.

• (4) Corresponding to every classical observables, there exists a quantum mechanical operator. (Which we have previously discussed)

• (5) A physically observable quantity can be represented by a Hermitian operator. An operator  is said to be Hermitian if it satisfies the following condition -
  

  

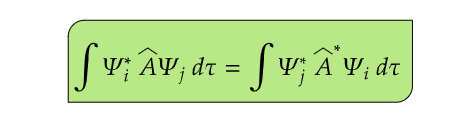
The significance of Hermitian operators is linked to the nature of physical observables in quantum mechanics. According to the postulates of quantum mechanics, physical observables, such as position, momentum, energy, and angular momentum, are represented by Hermitian operators.

• (6) The measurement of a observable generates some eigenvalues which are given by the eigenvalue equation-
  

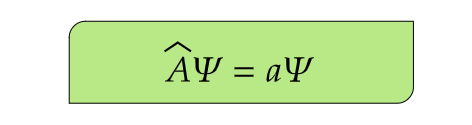
This property ensures that the expectation values of physical observables are real, which is essential for a meaningful interpretation in the context of measurements.

• (7) The average value (or expectation value) of an observable corresponding to some operator  is represented by the symbol <Â>

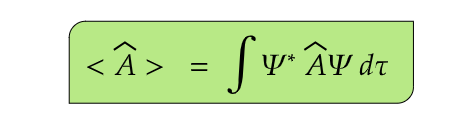
Here, the function Ψ is assumed to be normalized in accodance with postulate (3)

Normalization of Wavefunction

As already discussed, normalization means to bring a wavefunction to its normalized state. The normalization condition ensures that when considering all possible positions, the total probability of finding the particle is 1, representing certainty that the particle exists somewhere.

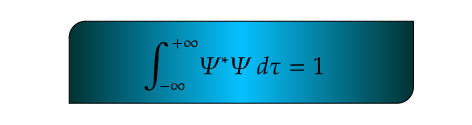
How to normalize a wavefunction?

Normalizing a wavefunction is a crucial step in quantum mechanics to ensure that the probability density associated with the wavefunction is well-defined and integrates to unity over all possible positions. The normalization condition for a one-dimensional wavefunction Ψ is given by:

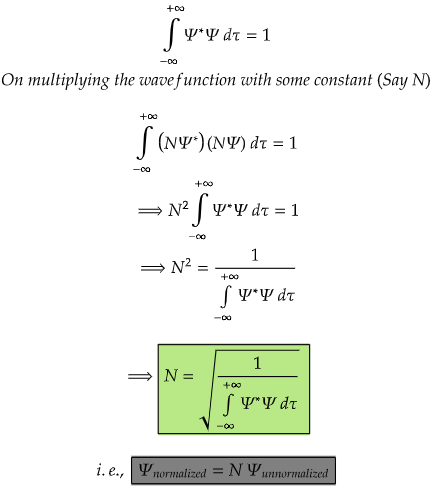
The most important step in normalizing a wavefunction is to multiply the wavefunction with some constant called normalization constant.(here, N is a normalization constant)

For a function to be normalizable, it should vanish at or disappear at -∞ and +∞.

Problem) Consider a wavefunction Ψ = e^imφ for a rigid rotor in between (0 ≤ φ ≤ 2π). Find out whether it is normalized or not? If not make it normalized.

Solution

Let's check if the wavefunction is normalized or not! We know the condition.

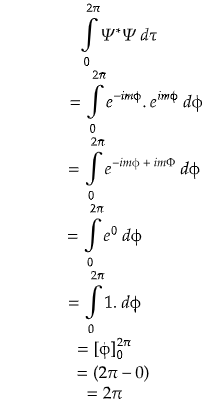
Since, the result is not unity, so clearly the given wavefunction is in an unnormalized form.

Now, let us find the value of normalization constant which is crucial for normalization process.

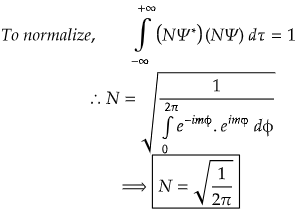
We have got the value of normalization constant.

∵ Ψ_normalized = N Ψ_unnormalized
∴ Ψ_normalized = (1/√2π) e^imφ

Proof

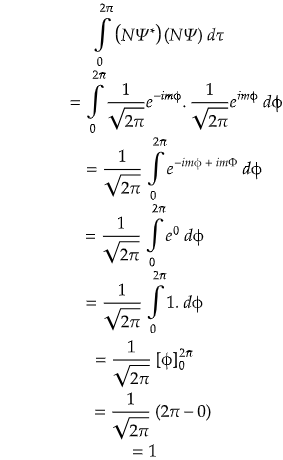
As it satisfies the normalization condition, hence it is proved.

What we learnt?

• We studied wave particle duality of electron through de Broglie wave equation. Discussed various other forms that could be form from the de Broglie wave equation.

• Discussed postulates of quantum mechanics. The formulation of quantum mechanics or wave mechanics for the wave mechanical treatment of the structure of atom rests upon these postulates.

• Studied normalization of wavefunction, process of normalizing a wavefunction and how crucial normalization constants are for normalization process.

Software used:

The mathematical equations are prepared using mathcha.io editor.

---

Read My Previous Blogs:

---

Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|

How to find Expression of an Operator and Commutation Relations |ChemFam #76|

Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|

Exploring Total Differentials and Cyclic Rules as Mathematical Maestros in Thermodynamics |ChemFam #74|

A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|

A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|

Decoding Liver Function Tests through Chemistry |ChemFam #71|

Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|

Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|

Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|

The Silent Revolution: How Polymers are Shaping Our World? |ChemFam #67|

Beyond the Bin: The Many Faces of Plastic Management |ChemFam #66|

Spectrophotometry Simplified: The Beer-Lambert Law in Spectrophotometry |ChemFam #65|

Chromatography: Unraveling the Science of Separation |ChemFam #64|

Colorful Clues: The Magical World of Chemical Indicators |ChemFam #63|

Colloids in Action: Impacting Your Daily Life More Than You Think |ChemFam #62|

The Complex Landscape of Opioid Analgesics: Addressing The Concerns |ChemFam #61|

Genetic Engineering: Pioneering Progress or Ethical Predicament? |ChemFam #60|

The Guardians Against Microbial Menace: Antibacterial Agents |ChemFam #59|

The Cholesterol Conundrum: The Story of Statins |ChemFam #58|

Unveiling The Control Of Chemistry: How Hormones Dictate Our Mood |ChemFam #57|

Thermodynamic Versus Kinetic Control of Reactions |ChemFam #56|

Bosons: The Quantum Glue That Holds The Universe Together |ChemFam #55|

PS The thumbnail image is being created by me using canva.com and a template from Image by Gerd Altmann from Pixabay

---

Thanks for stopping by :)