How to find Expression of an Operator and Commutation Relations |ChemFam #76|
Greetings to everyone! We have studied basics of quantum chemistry in the previous blog. We understood what operators, functions and some key properties of operators. Today, we shall study expression for operator. The expression of operators in quantum mechanics is a fascinating aspect that unveils the elegant language through which we comprehend the behavior of particles at the quantum level.

Operators are entities that act on quantum states, transforming one state into another. The expression for an operator can be derived by operating the operator on some operand and removing the operand at the last of the operation.
We can see this by taking an example of finding the expression for the operator [d/dx̂+x̂]2
As we have already studied in previous blogs that operator without a function is meaningless.
So, let us assume a function Ψ
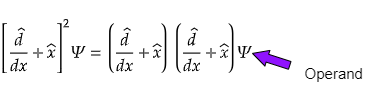
Here, Ψ is an operand and we are going to remove it at the end of the operation to find the expression for the given operator. An operand is nothing but a function over which operator is applied.

This is the final expression for the given operator.
Let us now do another problem.
Problem) Find the expression for the operator (d̂/dx - x̂)(d̂/dx + x̂)
Solution
Let us again take an another operand Ψ to carry out the operation. We will remove the operand at the end to find out the expression for the operator.

This is the expression for the said operator.
Commutations of an operator
One of the striking features of operators in quantum mechanics is the concept of commutation relations. The commutator of two operators  and B̂, denoted by [Â, B̂], is defined as AB - BA. Commutation relations play a crucial role in understanding the uncertainties associated with certain pairs of observables, as elucidated by Heisenberg's uncertainty principle.
For two operators  and B̂, if commutation of Â,B̂ i.e.,
[Â, B̂] = 0, we can calculate both the values at the same time. This means they commute with each other.
or [Â, B̂] ≠ 0, we can not calculate both the values at the same time. This means that they does not commute with each other.
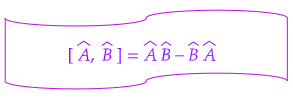
Let us understand how to apply commutations of an operator by taking the following example.

Problem) Prove that [Â, B̂]=-[B̂, Â]
Solution
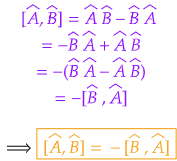
Now, I am going to share some tricks or basically short-cut methods to find commutation of operators.
Short-cut method
If the first operator is of differentiation and the second operator is of any power of x, then we just need to differentiate it with respect to x.

let us find the commutation of position and momentum operator-

Both these values are very important for easy calculations in quantum chemistry. So in future I will simply put the values. It's good if you remember the values.
Now, for position and linear momentum operators, we can use the following trick-

What we learnt?
- We studied the expression for an operator. We found that an operand is essential to carry out the expression for an operator. In the end, we can remove the operand. The operand provides a medium for the calculations as an operator is meaningless without a function.
- We studied commutations of an operator. When and how two operators commute with each other
- Apart from it, we have also studied some short-cut methods to determine commutations of operators.
Software used:
The mathematical equations are prepared using mathcha.io editor.

Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|
A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|
A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|
Decoding Liver Function Tests through Chemistry |ChemFam #71|
Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|
Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|
Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|
The Silent Revolution: How Polymers are Shaping Our World? |ChemFam #67|
Beyond the Bin: The Many Faces of Plastic Management |ChemFam #66|
Spectrophotometry Simplified: The Beer-Lambert Law in Spectrophotometry |ChemFam #65|
Chromatography: Unraveling the Science of Separation |ChemFam #64|
Colorful Clues: The Magical World of Chemical Indicators |ChemFam #63|
Colloids in Action: Impacting Your Daily Life More Than You Think |ChemFam #62|
The Complex Landscape of Opioid Analgesics: Addressing The Concerns |ChemFam #61|
Genetic Engineering: Pioneering Progress or Ethical Predicament? |ChemFam #60|
The Guardians Against Microbial Menace: Antibacterial Agents |ChemFam #59|
The Cholesterol Conundrum: The Story of Statins |ChemFam #58|
Unveiling The Control Of Chemistry: How Hormones Dictate Our Mood |ChemFam #57|
Thermodynamic Versus Kinetic Control of Reactions |ChemFam #56|
Bosons: The Quantum Glue That Holds The Universe Together |ChemFam #55|
PS The thumbnail image is being created by me using canva.com

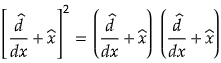

This post has been manually curated by @bhattg from Indiaunited community. Join us on our Discord Server.
Do you know that you can earn a passive income by delegating to @indiaunited. We share more than 100 % of the curation rewards with the delegators in the form of IUC tokens. HP delegators and IUC token holders also get upto 20% additional vote weight.
Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.
100% of the rewards from this comment goes to the curator for their manual curation efforts. Please encourage the curator @bhattg by upvoting this comment and support the community by voting the posts made by @indiaunited..
This post received an extra 2.15% vote for delegating HP / holding IUC tokens.
Yay! 🤗
Your content has been boosted with Ecency Points, by @splash-of-angs63.
Use Ecency daily to boost your growth on platform!
Hello,
this Comment has been upvoted with 50%, thanks to @splash-of-angs63 who burned 500 PLANET
With this burn @splash-of-angs63 is actively participating in the CLEAN PLANET reward protocol.
@splash-of-angs63 is helping @cleanplanet to grow with the curation.
Thanks for your help
@cleanplanet
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.
I haven't read any blog on Hive for a long time (being overwhelmed with many other things), and someone (@eniolw) pointed yours out to me. It is always a great pleasure to read about physics, especially when written by others.
Interestingly, I have never used the term 'operand' in the quantum mechanical context. Usually, I prefer to use 'wave functions' or 'state' (depending on the level of the audience). Anyway, your blog is nicely written and offers a good way to introduce some of the mathematical tools necessary to understand quantum mechanics. I hope that at some point in the future, you will make use of these mathematical tools to delve deeper into physics itself.
Cheers!
Prof. @lemouth Thank you so much for taking the time to have a glance at my post and thank you Prof. @eniolw for spotting and pointing it out (From the many you have to go through each day)
It's a pleasure for me that you liked my not so interesting content! (not for us, lol). Here, I am using the term operand (basically a function, as you said) just to make it significant that an operator needs a function to have a meaningful mathematical operation. I'll continue this series on quantum mechanics :)
I am definitely not going away from my field anytime soon (enrolled in PhD, so no choice, lol) :)