Exploring Time-Independent Schrödinger's Wave Equation and Particle in a 1D Box | ChemFam #80 |

Greetings to everyone! In my last blog we have studied about a very important mathematical tool i.e., gamma function. We have also discussed a rough idea about Schrödinger wave equation. Today, as promised previously, we will study thoroughly about Schrödinger wave equation. After discussing, we shall then see solution for Schrödinger wave equation for a simple system. We will restrict our discussions to particle in a one dimensional box for today.

Erwin Schrödinger, in 1926, gave a wave equation to describe the behaviour of electron waves in atoms and molecules. In Schrödinger's wave model of an atom, the discrete energy levels or orbits proposed by Bohr are replaced by mathematical functions, Ψ, which are related to the probability of finding electrons at various places around the nucleus.

From previous discussion on my post about eigenvalues and eigenfunction, we know that we have the time-independent Schrödinger wave equation as,

ĤΨ = EΨ

I hope you remember that here E is eigen value and Ψ is eigenfunction.

From the class on operators, we know that the Hamiltonian operator Ĥ is a comination of kinetic energy and potential energy. On putting the value of kinetic energy operator, and proceeding to solve it, we finally get as,

-
The above equation is the time-dependent Schrödinger wave equation.

The Schrödinger wave equation can be solved for different simple systems, such as particle in a 1d box, particle in a 2D box, 3d box, one dimensional simple harmonic oscillator or a rigid rotor. Let us see the solution of the Schrodinger wave equation for particle in a 1 dimensional box.

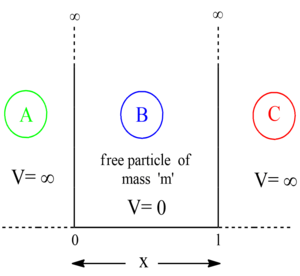
Particle in a 1D box

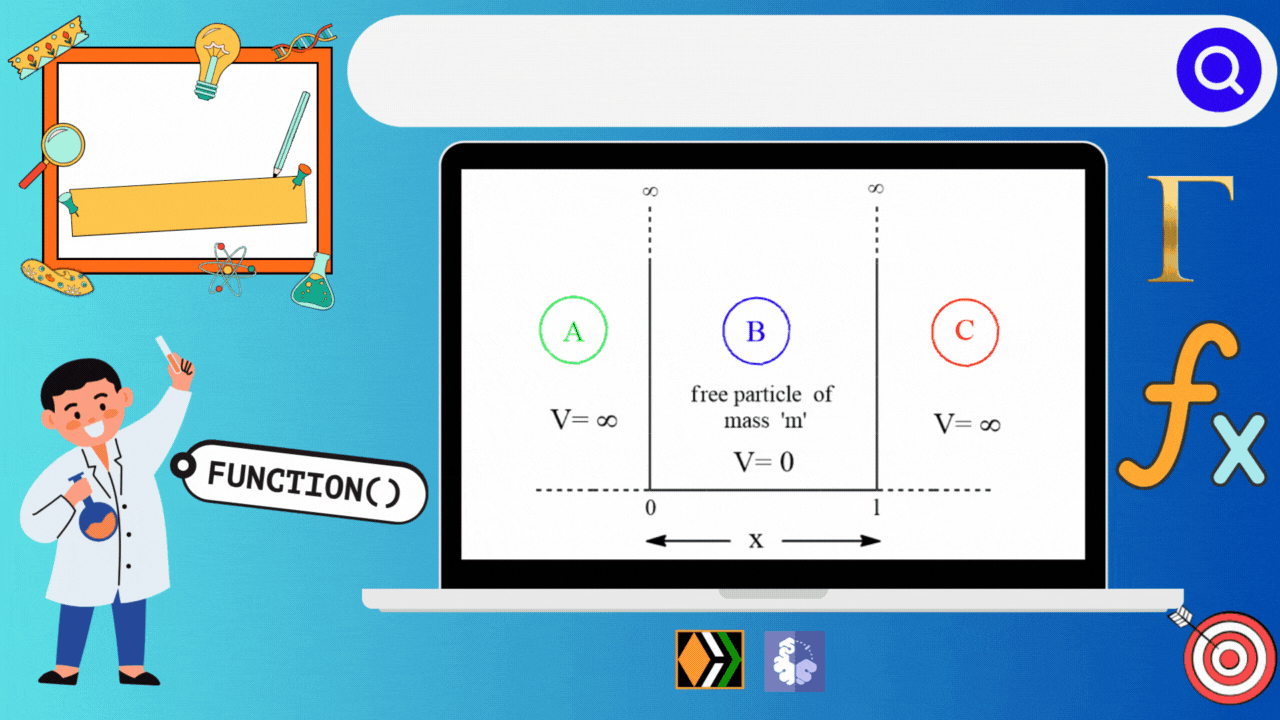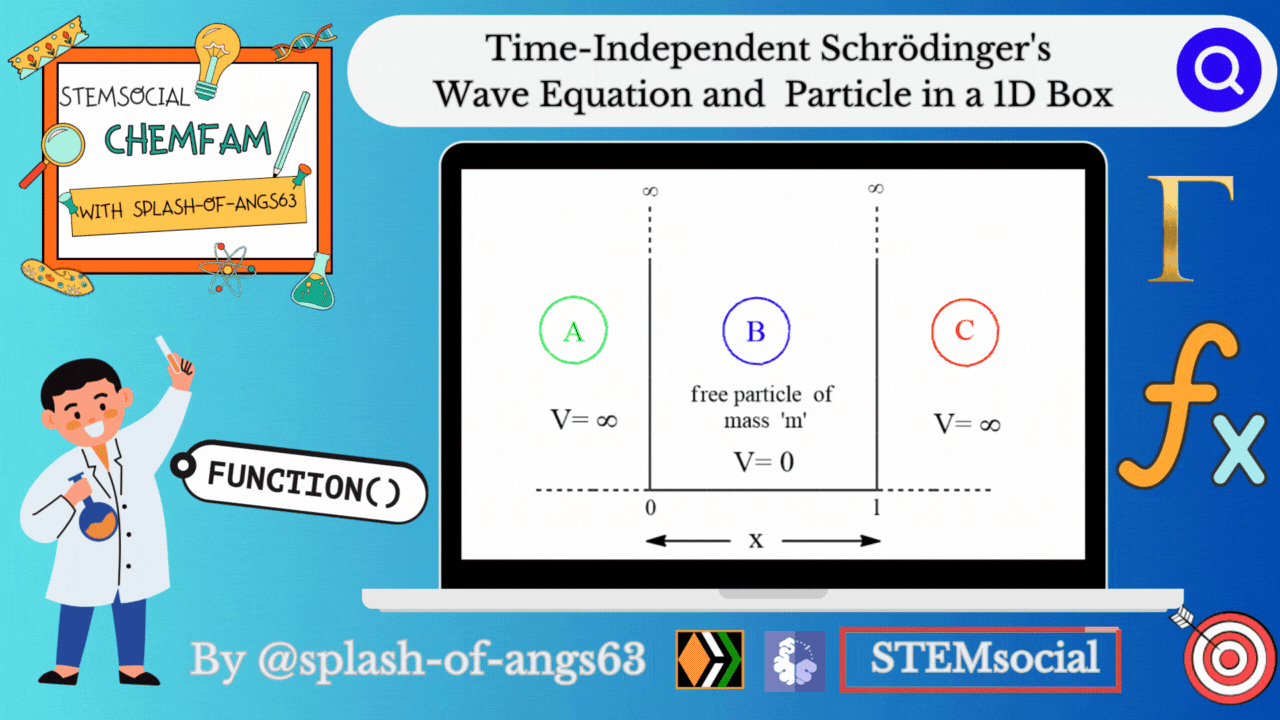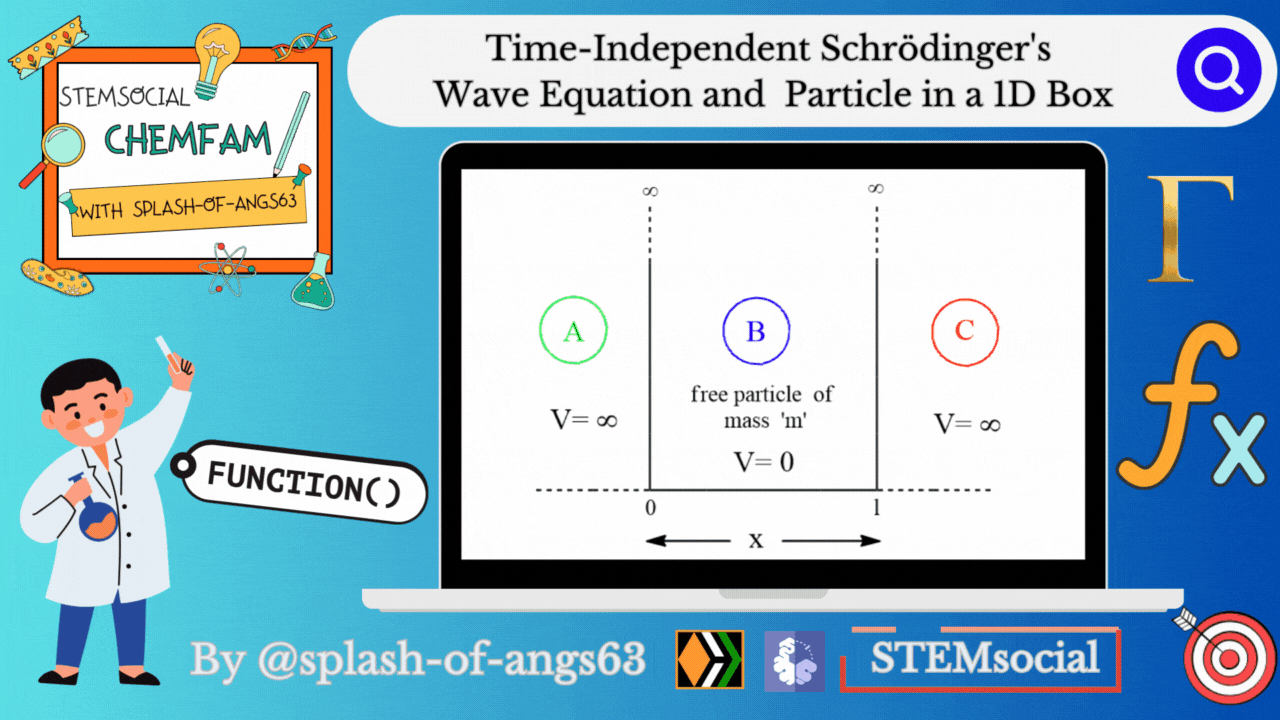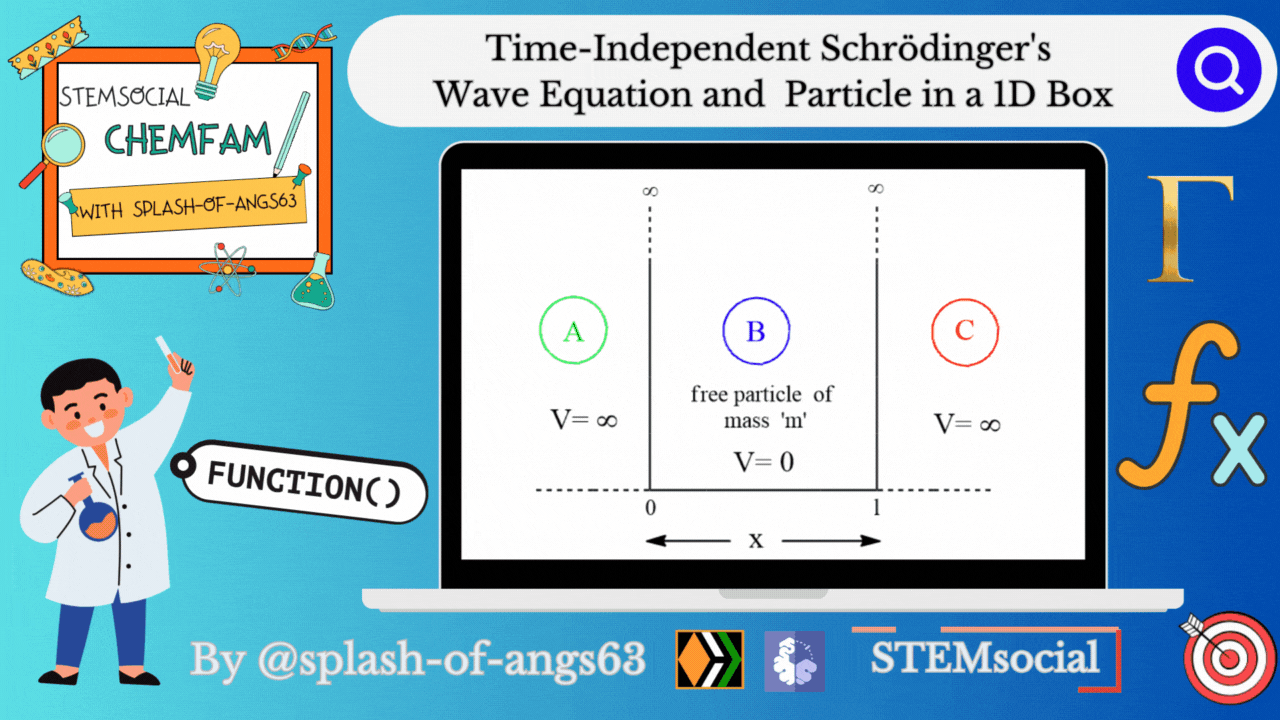
Let us consider a free particle of mass 'm' is moving in a asymmetric box which is bounded in between o to l.

There exists no force in a free particle, so F(force)=0 and also Potential(V)=0. The particle of mass 'm' is confined to move in a one dimensional box of width 'l' having infinitely high walls. This is the simplest quantum mechanical problem which represents translational motion. The particle is subjected to a potential energy function that is infinite everywhere along the x-axis except for a line segment of length 'l', where the potential is 0.

Let's mark all the three possible region that the particle could reside as A, B and C and examine them one by one.

Region B

Now, from time-independent Schrodinger equation (TISE), we have,

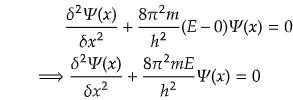
Since, the walls are of infinite length, i.e., the particle is definitely present within the walls. Remember? which condition does it satisfies? Yes! correct, it satisfies the condition of normalization. That means the particle is definitely present within the region B.

Region A and C

As the potential is ∞ in regions other than B, so again from the TISE, we have,

Since the avefunction Ψ(x)=0, so the probability of finding the particle outside the box is zero. Hence, the particle does not exists in region A and C.

Thus we can conclude that Ψ=0 outside the box and likewise Ψ=0 at the walls also, i.e., x=0 and x=l.

So, if the particle exists within the region B, there must be a solution to the wave equation. Let's solve and find the value of the wavefunction, Ψ(x)

Finding the solution

From the wave equation from region B, we have,

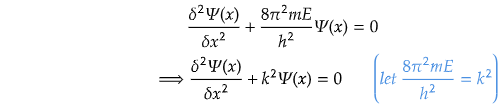
The above equation is an ordinary second order differential equation and has the solution of the form, Ψ(x)= A sin kx +B cos kx, where A and B are two arbitrary constants.

We need to verify the solution, then only we can be certain that we are doing the right thing.

Proof of the solution

As the values satisfies the equation, hence it is proved!

Now we have to check the boundary conditions too!

Boundary conditions

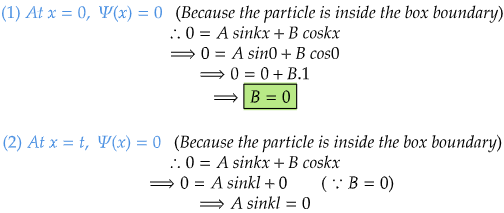
A can not be zero, cuz B=0 already and if both the arbitrary constants are zero, the wavefunction value will be 0, which can not be true for region B.

If A ≠ 0, then

Now, we have,

To find the normalization constant A, we will do what we have studied earlier.

-

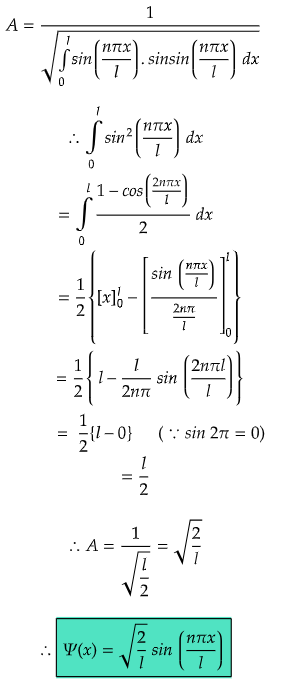Finding the energy eigenvalue

From the value of k, we can find out the energy eigenvalue.

-

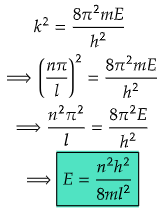Where,m = mass of the particle
l=length of the box
h=Planck's constant
and n=energy levels.

What we learnt?

• We studied the Schrodinger wave equation involving the total energy operator and the energy eigenvalue. We formulated the time independent Schrodinger wave equation. This form is called time independent as the potential, V is not a function of time, t but depends only on x.

• We studied the different possible regions in a 1D box to which the particle could possibly reside. We studied each regions separately and concluded the possibility of finding the particle in region B.

• We studied the solution to the Schrodinger wave equation considering the boundary conditions. We then, went onto find the important energy eigenvalue.

Software used:

The mathematical equations are prepared using mathcha.io editor and diagrams are drawn using ChemDraw software.

---

Read My Previous Blogs:

---

The Role of Gamma Function in Quantum Mechanics | ChemFam #79 |

Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|

Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|

How to find Expression of an Operator and Commutation Relations |ChemFam #76|

Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|

Exploring Total Differentials and Cyclic Rules as Mathematical Maestros in Thermodynamics |ChemFam #74|

A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|

A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|

Decoding Liver Function Tests through Chemistry |ChemFam #71|

Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|

Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|

Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|

The Silent Revolution: How Polymers are Shaping Our World? |ChemFam #67|

Beyond the Bin: The Many Faces of Plastic Management |ChemFam #66|

Spectrophotometry Simplified: The Beer-Lambert Law in Spectrophotometry |ChemFam #65|

Chromatography: Unraveling the Science of Separation |ChemFam #64|

Colorful Clues: The Magical World of Chemical Indicators |ChemFam #63|

Colloids in Action: Impacting Your Daily Life More Than You Think |ChemFam #62|

The Complex Landscape of Opioid Analgesics: Addressing The Concerns |ChemFam #61|

Genetic Engineering: Pioneering Progress or Ethical Predicament? |ChemFam #60|

The Guardians Against Microbial Menace: Antibacterial Agents |ChemFam #59|

The Cholesterol Conundrum: The Story of Statins |ChemFam #58|

Unveiling The Control Of Chemistry: How Hormones Dictate Our Mood |ChemFam #57|

Thermodynamic Versus Kinetic Control of Reactions |ChemFam #56|

Bosons: The Quantum Glue That Holds The Universe Together |ChemFam #55|

PS The thumbnail image is being created by me using canva.com

---

Games I play on Hive

Games I play on Hive	Game description
Terracore	Terracore is an Idle mining game based on Hive blockchain
Rise of the Pixels	ROTP is a Web3 browser game about game development on Hive

---

Thanks for stopping by :)