[ESP]

¡Hola, entusiastas de la electrónica en Hive! 👋

En nuestra serie sobre herramientas esenciales en electrónica digital, hoy nos adentramos en el uso y teoría de los Mapas de Karnaugh. Esta técnica matemática es fundamental para simplificar expresiones booleanas y optimizar el diseño de circuitos lógicos. 📚✨

¿Qué son los Mapas de Karnaugh? 🤔

Los Mapas de Karnaugh, desarrollados por Maurice Karnaugh en 1953, son una herramienta visual para simplificar expresiones booleanas con cuatro variables o menos. Facilitan la identificación de términos comunes en una expresión lógica, lo que permite simplificar la función lógica de manera más efectiva y eficiente que con el álgebra booleana tradicional.

Funcionamiento Básico 📊

• Configuración del Mapa: Un Mapa de Karnaugh se presenta en forma de una tabla de verdad en la que las variables se organizan para minimizar el número de cambios de grupo entre celdas adyacentes.
• Agrupación de Unos: Las celdas del mapa se llenan con unos (1) y ceros (0) según la tabla de verdad de la función. Luego, los unos se agrupan en bloques rectangulares que contienen números de celdas como potencias de dos (1, 2, 4, 8, etc.). Estas agrupaciones simplifican la función original.

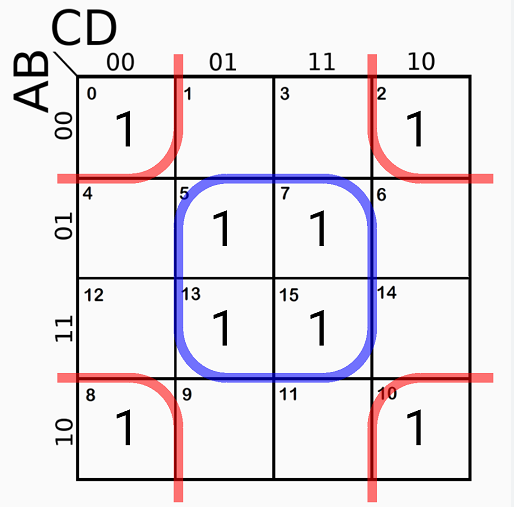
Aplicaciones Prácticas 🌍

• Diseño de Circuitos: Los Mapas de Karnaugh son ideales para el diseño de circuitos lógicos y digitales, permitiendo a los diseñadores ver las simplificaciones posibles de manera rápida y clara.
• Optimización de Hardware: Ayudan a reducir el número de puertas lógicas necesarias en un circuito, lo que puede llevar a ahorros significativos en costos y espacio en los dispositivos.
• Educación y Formación: Son una herramienta didáctica excelente para enseñar lógica y diseño de circuitos en educación en ingeniería y tecnología.

Ejemplo Práctico: Simplificación de un Circuito 🎛️

Supongamos que tienes un circuito con cuatro variables (W, X, Y, Z) y quieres simplificar la expresión booleana. Mediante el uso de un Mapa de Karnaugh, puedes organizar las variables y visualizar las posibles simplificaciones directamente, facilitando la creación de un diseño de circuito más eficiente.

---

---

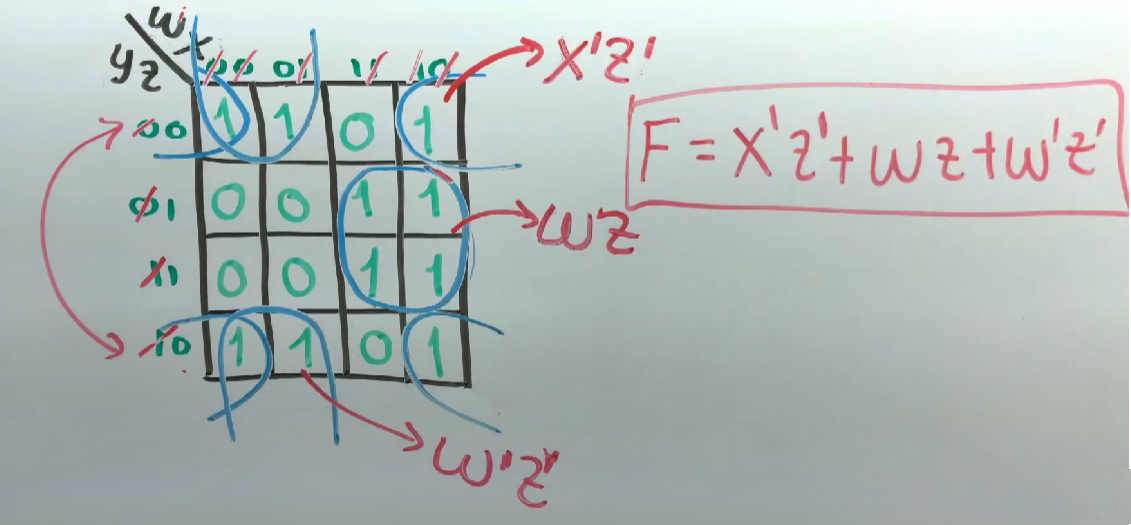
📢 ¡Gracias por descubrir los Mapas de Karnaugh conmigo! 📘

Espero que este post te haya ofrecido una clara comprensión de cómo esta poderosa herramienta puede facilitar y mejorar el diseño de tus proyectos electrónicos. Si tienes preguntas o ejemplos propios de cómo los has utilizado, ¡comparte tus experiencias en los comentarios! 📝

🔔 Sigue atento a más contenidos educativos donde continuaremos explorando otras herramientas y técnicas vitales en el campo de la electrónica digital. 🌐

🤝 Conéctate en redes sociales para unirte a debates y compartir tus proyectos con una comunidad de entusiastas como tú. ¡Tu participación fortalece nuestro aprendizaje colectivo! 💬

📷 Comparte tus proyectos: Si has aplicado los Mapas de Karnaugh en la simplificación de circuitos, ¡nos encantaría ver tus creaciones! 🛠️

🌟 Mantente activo en la comunidad: No olvides seguirme para no perderte ningún contenido que pueda inspirarte y ayudarte a avanzar en tus proyectos. 🚀✨

¡Hasta la próxima, sigue diseñando, aprendiendo y creciendo!

---

---

---

[ENG]

Hello, electronics enthusiasts at Hive! 👋

In our series on essential tools in digital electronics, today we delve into the use and theory of Karnaugh Maps. This mathematical technique is essential for simplifying Boolean expressions and optimizing the design of logic circuits. 📚✨

What are Karnaugh Maps? 🤔

Karnaugh Maps, developed by Maurice Karnaugh in 1953, are a visual tool for simplifying Boolean expressions with four or fewer variables. They make it easier to identify common terms in a logical expression, allowing the logical function to be simplified more effectively and efficiently than with traditional Boolean algebra.

Basic Operation 📊

• Map Setup: A Karnaugh Map is presented in the form of a truth table in which variables are arranged to minimize the number of group shifts between adjacent cells.
• Grouping of Ones: The cells of the map are filled with ones (1) and zeros (0) according to the truth table of the function. The ones are then grouped into rectangular blocks containing cell numbers as powers of two (1, 2, 4, 8, etc.). These groupings simplify the original function.

Practical Applications 🌍

• Circuit Design: Karnaugh Maps are ideal for the design of logic and digital circuits, allowing designers to see possible simplifications quickly and clearly.
• Hardware Optimization: They help reduce the number of logic gates needed in a circuit, which can lead to significant savings in cost and space on devices.
• Education and Training: They are an excellent teaching tool for teaching logic and circuit design in engineering and technology education.

Practical Example: Simplifying a Circuit 🎛️

Suppose you have a circuit with four variables (W, X, Y, Z) and you want to simplify the boolean expression. By using a Karnaugh Map, you can organize variables and visualize possible simplifications directly, making it easier to create a more efficient circuit design.

---

---

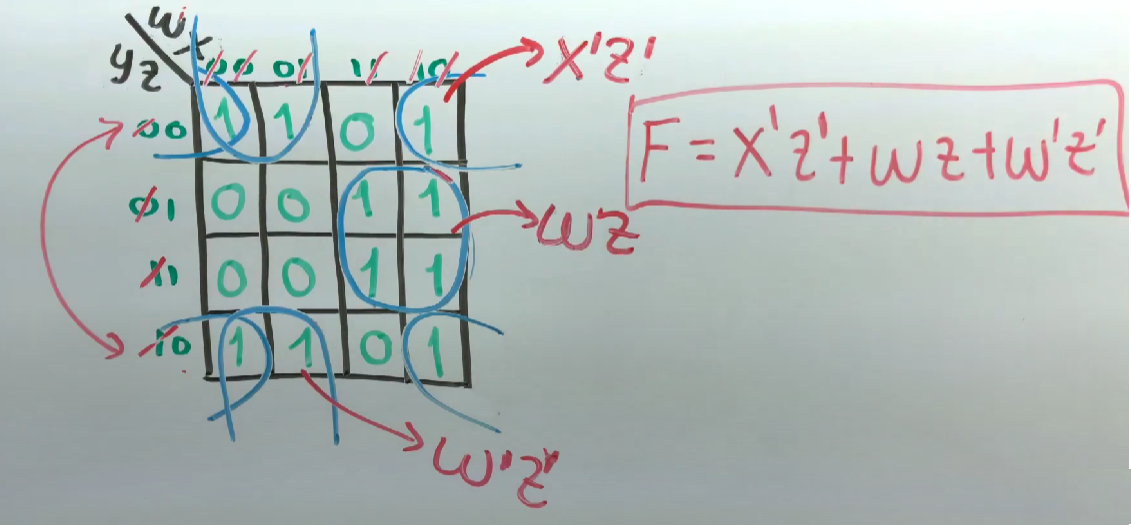
📢 Thanks for discovering Karnaugh Maps with me! 📘

I hope this post has given you a clear understanding of how this powerful tool can facilitate and improve the design of your electronic projects. If you have questions or examples of your own of how you've used them, please share your experiences in the comments! 📝

🔔 Stay tuned for more educational content where we'll continue to explore other vital tools and techniques in the field of digital electronics. 🌐

🤝 Connect on social media to join discussions and share your projects with a community of enthusiasts like you. Your participation strengthens our collective learning! 💬

📷 Share your projects: If you have applied Karnaugh Maps to simplify circuits, we would love to see your creations! 🛠️

🌟 Stay active in the community: Don't forget to follow me so you don't miss any content that can inspire you and help you advance in your projects. 🚀✨

Until next time, keep designing, learning and growing!