[ESP/ENG] 🖥️🔧Álgebra Booleana y Simplificación de Expresiones Lógicas: Claves para la Eficiencia en Electrónica Digital 🖥️🔧Boolean Algebra and Simplification of Logical Expressions: Keys to Efficiency in Digital Electronics
[ESP]
¡Saludos, comunidad de Hive! 👋
Hoy vamos a sumergirnos en el fascinante mundo del Álgebra Booleana y la simplificación de expresiones lógicas, elementos fundamentales en el diseño y análisis de circuitos electrónicos digitales. 📚✨

¿Qué es el Álgebra Booleana? 🤔
El álgebra booleana es un área de la matemática que se ocupa de las variables binarias y las operaciones lógicas. Nombrada así por George Boole, un matemático del siglo XIX, esta teoría forma la base de la electrónica digital moderna, permitiendo la construcción de circuitos lógicos y computadoras.
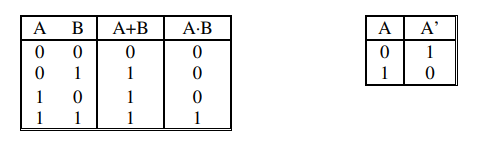
Operaciones Básicas del Álgebra Booleana 📊
- AND (Y): Produce un 1 solo si todos los operandos son 1.
- OR (O): Produce un 1 si al menos uno de los operandos es 1.
- NOT (NO): Invierte el valor del operando; si es 1, devuelve 0 y viceversa.
Simplificación de Expresiones Lógicas ⚙️
La simplificación de expresiones lógicas es crucial para optimizar el diseño de circuitos, reduciendo la cantidad de puertas lógicas necesarias, lo que se traduce en menor consumo de energía, menor espacio y mayor velocidad de procesamiento.
- Métodos de Simplificación: Se utilizan métodos como la tabla de verdad, mapas de Karnaugh o las leyes y teoremas del álgebra booleana para simplificar expresiones y hacer circuitos más eficientes.
Importancia del Álgebra Booleana y la Simplificación 🌟
- Eficiencia en Diseño: Permite diseñar circuitos más simples y eficientes.
- Reducción de Costos y Espacio: Minimiza los recursos necesarios para la construcción de dispositivos electrónicos.
- Mejora del Rendimiento: Circuitos simplificados significan mayor velocidad de operación y menor consumo de energía.
Ejemplo Práctico: Simplificación de un Circuito 🎛️
Imagina que necesitas diseñar un circuito que active una alarma si se detecta movimiento (M) o si se rompe un cristal (C). La expresión inicial podría ser M OR C. Sin embargo, si se añaden más condiciones y sensores, el proceso de simplificación ayudará a reducir la complejidad del diseño final.
📢 ¡Gracias por explorar el álgebra booleana y la simplificación de expresiones conmigo! 📘
Espero que este post te haya ayudado a comprender mejor cómo las matemáticas se aplican en la práctica a la tecnología que usamos todos los días. Si tienes preguntas o deseas compartir tus experiencias, por favor, comenta abajo. 📝
🔔 No te pierdas futuras publicaciones donde seguiremos desglosando conceptos complejos en lecciones comprensibles y aplicables. 🌐
🤝 Conéctate en redes sociales para más discusiones y recursos educativos en electrónica y matemáticas. 💬
📷 Comparte tus proyectos: Si has diseñado circuitos utilizando álgebra booleana o simplificado expresiones para tus creaciones, ¡nos encantaría verlas! 🛠️
🌟 Sigue activo en la comunidad: Mantente conectado para no perderte ningún contenido que te ayude a crecer profesional y personalmente en el campo de la electrónica digital. 🚀✨
¡Hasta la próxima, sigue innovando y compartiendo tus logros!
[ENG]
Greetings, Hive community! 👋
Today we are going to dive into the fascinating world of Boolean Algebra and the simplification of logical expressions, fundamental elements in the design and analysis of digital electronic circuits. 📚✨

What is Boolean Algebra? 🤔
Boolean algebra is an area of mathematics that deals with binary variables and logical operations. Named after George Boole, a 19th-century mathematician, this theory forms the basis of modern digital electronics, allowing the construction of logic circuits and computers.

Basic Operations of Boolean Algebra 📊
- AND: Produces a 1 only if all operands are 1.
- OR: Produces a 1 if at least one of the operands is 1.
- NOT: Inverts the value of the operand; if it is 1, it returns 0 and vice versa.
Simplification of Logical Expressions ⚙️
The simplification of logical expressions is crucial to optimize the design of circuits, reducing the number of logic gates needed, which translates into lower power consumption, less space and higher processing speed.
- Simplification Methods: Methods such as the truth table, Karnaugh maps, or the laws and theorems of Boolean algebra are used to simplify expressions and make circuits more efficient.
Importance of Boolean Algebra and Simplification 🌟
- Design Efficiency: Allows for the design of simpler and more efficient circuits.
- Cost and Space Reduction: Minimizes the resources needed to build electronic devices.
- Performance Improvement: Simplified circuits mean faster operation and lower energy consumption.
Practical Example: Simplifying a Circuit 🎛️
Imagine that you need to design a circuit that activates an alarm if motion is detected (M) or if a glass is broken (C). The initial expression could be M OR C. However, if more conditions and sensors are added, the simplification process will help reduce the complexity of the final design.
📢 Thank you for exploring Boolean algebra and simplifying expressions with me! 📘
I hope this post helped you better understand how math is practically applied to the technology we use every day. If you have questions or want to share your experiences, please comment below. 📝
🔔 Don't miss future posts where we will continue to break down complex concepts into understandable and applicable lessons. 🌐
🤝 Connect on social media for more discussions and educational resources on electronics and math. 💬
📷 Share your projects: If you have designed circuits using Boolean algebra or simplified expressions for your creations, we would love to see them! 🛠️
🌟 Stay active in the community: Stay connected so you don't miss out on any content that helps you grow professionally and personally in the field of digital electronics. 🚀✨