[ESP]

¡Hola, visionarios digitales de Hive! 👋

Continuando con nuestra exploración de los sistemas de numeración, hoy abordaremos cómo convertir números entre diferentes sistemas—binario, octal, hexadecimal y decimal. Este conocimiento es crucial para diseñadores de software, programadores y cualquier persona interesada en la informática y la electrónica. 🚀📚

¿Por qué Convertir Sistemas de Numeración? 🤔

La conversión entre diferentes sistemas de numeración es esencial porque permite la interoperabilidad entre diversas plataformas y sistemas que utilizan distintas bases numéricas para operar.

Métodos de Conversión Básicos 📖

Binario a Decimal:

• Método: Multiplica cada bit del número binario por el valor de 2 elevado a su posición, empezando desde 0 a la derecha. Suma todos los resultados para obtener el equivalente decimal.
• Ejemplo: Convertir 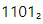a decimal. Calcula: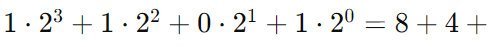

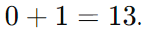
Decimal a Binario:

• Método: Divide el número decimal entre 2. El resto es el bit más a la derecha (LSB). Continúa con el cociente hasta que sea 0.
• Ejemplo: Convertir 13 a binario. División sucesiva por 2 da 1101₂.

Hexadecimal a Decimal:

• Método: Similar al binario a decimal, pero multiplica cada dígito por 16 elevado a su posición.
• Ejemplo: Convertir 1A₁₆ a decimal. Calcula
  

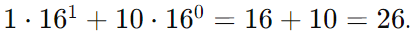
Decimal a Hexadecimal:

• Método: Divide el número decimal entre 16. El resto es el dígito más a la derecha. Repite con el cociente hasta que sea 0.
• Ejemplo: Convertir 26 a hexadecimal. División sucesiva por 16 da 1A₁₆.

Aplicaciones Prácticas 🌍

• Desarrollo de Software: La conversión es utilizada en el desarrollo de aplicaciones que interactúan con hardware o sistemas de bajo nivel que requieren formatos numéricos específicos.
• Comunicaciones y Redes: Protocolos de red a menudo utilizan hexadecimal para representar direcciones y otros datos.
• Cifrado y Seguridad: Las técnicas de cifrado frecuentemente operan en diferentes bases numéricas para realizar transformaciones de datos.

---

---

📢 ¡Gracias por acompañarme en esta lección de conversión numérica! 📘

Espero que este tutorial te haya equipado mejor para manejar diversas bases numéricas en tus proyectos y desafíos tecnológicos. Si tienes alguna pregunta o quieres compartir cómo utilizas estas conversiones en la práctica, ¡deja un comentario abajo! 📝

🔔 Sigue atento a futuros posts donde seguiremos desentrañando los misterios de la tecnología y la informática. 🌐

🤝 Únete a nuestra comunidad en redes sociales para más intercambios educativos y enriquecedores. 💬

📷 Comparte tus proyectos: Si has implementado estas técnicas de conversión en tu trabajo o estudios, ¡nos encantaría ver tus resultados! 🛠️

🌟 Mantente activo y comprometido: Sigue esta cuenta para obtener contenido continuo que te inspire y ayude en tus aventuras tecnológicas. 🚀✨

¡Hasta la próxima, sigue aprendiendo, explorando y compartiendo tus descubrimientos!

---

---

---

[ENG]

Hello, Hive digital visionaries! 👋

Continuing our exploration of number systems, today we'll cover how to convert numbers between different systems—binary, octal, hexadecimal, and decimal. This knowledge is crucial for software designers, programmers, and anyone interested in computing and electronics. 🚀📚

Why Convert Number Systems? 🤔

Converting between different number systems is essential because it allows for interoperability between various platforms and systems that use different number bases to operate.

Basic Conversion Methods 📖

Binary to Decimal:

• Method: Multiply each bit of the binary number by the value of 2 raised to its position, starting from 0 on the right. Add all the results together to get the decimal equivalent.
• Example: Convert 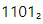to decimal. Calculate: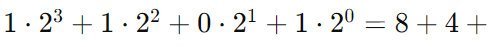

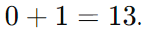
Decimal to Binary:

• Method: Divide the decimal number by 2. The remainder is the rightmost bit (LSB). Continue with the quotient until it is 0.
• Example: Convert 13 to binary. Successive division by 2 gives 1101₂.

Hexadecimal to Decimal:

• Method: Similar to binary to decimal, but multiply each digit by 16 raised to its position.
• Example: Convert 1A₁₆ to decimal. Calculate
  

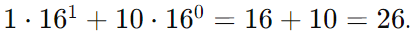
Decimal to Hexadecimal:

• Method: Divide the decimal number by 16. The remainder is the rightmost digit. Repeat with the quotient until it is 0.
• Example: Convert 26 to hexadecimal. Successive division by 16 gives 1A₁₆.

Practical Applications 🌍

• Software Development: Conversion is used in the development of applications that interact with hardware or low-level systems that require specific numeric formats.
• Communications and Networking: Network protocols often use hexadecimal to represent addresses and other data.
• Encryption and Security: Encryption techniques frequently operate on different number bases to perform data transformations.

---

---

📢 Thanks for joining me for this numeric conversion lesson! 📘

I hope this tutorial has better equipped you to handle various number bases in your projects and technological challenges. If you have any questions or want to share how you use these conversions in practice, leave a comment below! 📝

🔔 Stay tuned for future posts where we will continue to unravel the mysteries of technology and computing. 🌐

🤝 Join our community on social media for more educational and enriching exchanges. 💬

📷 Share your projects: If you've implemented these conversion techniques in your work or studies, we'd love to see your results! 🛠️

🌟 Stay active and engaged: Follow this account for ongoing content to inspire and help you on your tech adventures. 🚀✨

Until next time, keep learning, exploring, and sharing your discoveries!