[ESP]

¡Saludos, entusiastas de la electrónica y la informática de Hive! 👋

Hoy vamos a profundizar en la Aritmética Binaria, específicamente en las operaciones de suma y resta, esenciales para el procesamiento de datos y la lógica computacional. Estas operaciones son la base de todas las funciones más complejas que realizan nuestras computadoras y dispositivos digitales. 🚀📚

Fundamentos de la Aritmética Binaria 🤔

La aritmética binaria opera con números en base 2, utilizando solo dos dígitos, 0 y 1. Cada dígito en un número binario se llama bit. En el corazón de la computación, entender cómo se suman y restan estos bits es crucial para el diseño de circuitos y la programación.

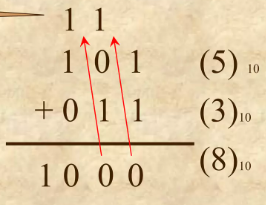
Suma Binaria ⚙️

Reglas Básicas:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10 (0 con acarreo de 1)

Ejemplo Práctico:

• Considera la suma de dos números binarios, 1101₂ y 1011₂:
  Comenzando desde la derecha, 1 + 1 = 10. Escribes 0 y acarreas 1.
• Continúas con 0 + 1 + 1 (acarreo) = 10. Escribes 0 y acarreas 1.

Repites el proceso hasta el final del número.

Resta Binaria 🛠️

Reglas Básicas:

0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 (con un préstamo de 1 del siguiente bit más significativo)

Ejemplo Práctico:

Considera restar 1001₂ de 1101₂:
Comenzando desde la derecha, 1 - 1 = 0.
0 - 0 = 0.
1 - 0 = 1 (sin necesidad de préstamo).
1 - 1 = 0.

Aplicaciones Prácticas 🌍

• Computación: Todas las operaciones en una computadora, desde cálculos simples hasta complejas simulaciones, dependen de la suma y resta binaria.
• Desarrollo de Hardware: Los diseñadores de circuitos utilizan estas operaciones para crear chips más eficientes para procesadores y dispositivos de almacenamiento.
• Educación y Formación: Fundamental para estudiantes de ciencias de la computación y electrónica, proporcionando la base para entender operaciones más avanzadas.

---

---

📢 ¡Gracias por sumergirte en la aritmética binaria conmigo! 📘

Espero que esta explicación te haya ayudado a comprender mejor cómo funcionan las operaciones básicas en el sistema binario. Si tienes alguna pregunta o quieres compartir cómo aplicas estos conocimientos en tus proyectos, ¡deja un comentario abajo! 📝

🔔 Mantente atento a futuros posts donde seguiremos desglosando los misterios de la tecnología y la informática. 🌐

🤝 Únete a la conversación en redes sociales para más intercambios educativos y enriquecedores. 💬

📷 Comparte tus proyectos: Si has implementado operaciones binarias en tus diseños o desarrollos, ¡queremos ver tus creaciones! 🛠️

🌟 Sigue activo en la comunidad: No olvides seguir esta cuenta para obtener contenido continuo que te inspire y ayude en tus aventuras tecnológicas. 🚀✨

¡Hasta la próxima, sigue aprendiendo, explorando y compartiendo tus descubrimientos!

---

---

---

[ENG]

Greetings, Hive electronics and computer enthusiasts! 👋

Today we're going to dive deeper into Binary Arithmetic, specifically the addition and subtraction operations, essential for data processing and computational logic. These operations are the foundation of all the more complex functions our computers and digital devices perform. 🚀📚

Binary Arithmetic Basics 🤔

Binary arithmetic operates on numbers in base 2, using only two digits, 0 and 1. Each digit in a binary number is called a bit. At the heart of computing, understanding how these bits add and subtract is crucial to circuit design and programming.

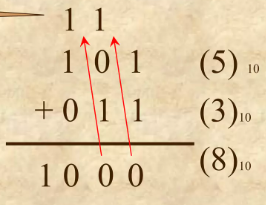
Binary Addition ⚙️

Basic Rules:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10 (0 with a carry of 1)

Practical Example:

• Consider the sum of two binary numbers, 1101₂ and 1011₂:
  Starting from the right, 1 + 1 = 10. You write 0 and carry 1.
• You continue with 0 + 1 + 1 (carry) = 10. You write 0 and carry 1.

You repeat the process until the end of the number.

Binary Subtraction 🛠️

Basic Rules:

0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 (with a borrow of 1 from the next most significant bit)

Practical Example:

Consider subtracting 1001₂ from 1101₂:
Starting from the right, 1 - 1 = 0.
0 - 0 = 0.
1 - 0 = 1 (no borrowing required).
1 - 1 = 0.

Practical Applications 🌍

• Computing: All operations on a computer, from simple calculations to complex simulations, rely on binary addition and subtraction.
• Hardware Development: Circuit designers use these operations to create more efficient chips for processors and storage devices.
• Education and Training: Fundamental for students of computer science and electronics, providing the foundation for understanding more advanced operations.

---

---

📢 Thanks for diving into binary arithmetic with me! 📘

I hope this explanation has helped you better understand how basic operations work in the binary system. If you have any questions or want to share how you apply this knowledge in your projects, leave a comment below! 📝

🔔 Stay tuned for future posts where we will continue to break down the mysteries of technology and computing. 🌐

🤝 Join the conversation on social media for more educational and enriching exchanges. 💬

📷 Share your projects: If you have implemented binary operations in your designs or developments, we want to see your creations! 🛠️

🌟 Stay active in the community: Don't forget to follow this account for ongoing content to inspire and help you on your tech adventures. 🚀✨

Until next time, keep learning, exploring, and sharing your discoveries!