Primera Ley de Kirchhoff (Ley de Corrientes de Kirchhoff)

La Primera Ley de Kirchhoff, también conocida como la Ley de Corrientes de Kirchhoff (KCL, por sus siglas en inglés), se basa en el principio de conservación de la carga eléctrica. Esta ley establece que:

En cualquier nodo de un circuito eléctrico, la suma algebraica de todas las corrientes que entran y salen del nodo es igual a cero.

Matemáticamente:

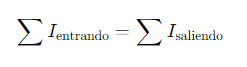(1)

o simplemente:

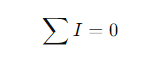
Para qué sirve

Esta ley es útil para Analizar lazos en circuitos complejos cmo la combinacion entre circuitos series y paralelos de resistencias; Permite determinar las tensiones o corrientes desconocidas en un circuito aplicando la ley de Ohm, si no la recordas te invito a que entres a mi blog que lo explico al detalle. Tambien ayuda a asegurar que la energía se conserva y las tensiones se distribuyen adecuadamente.

¿Cómo se usa?

Primero debemos poder identificar cuantos nodos hay en nuestro circuito, y para ello tenes que encontrar los puntos en el circuito donde dos o más componentes están conectados. Ya que la definicion de un nodo es:

Un Nodo es un punto en el circuito en el cual entran o salen tres corrientes o mas, por estar conectados a dos o mas componentes

• Asignar corrientes: Define una dirección para cada corriente que entra o sale del nodo (puede ser arbitraria; si se elige incorrectamente, el resultado será negativo, indicando la dirección opuesta).
• Aplicar KCL: Escribe una ecuación para cada nodo, sumando las corrientes que entran y restando las que salen.
  Resolver el sistema de ecuaciones: Utiliza las ecuaciones obtenidas para resolver las corrientes desconocidas.

Ejemplo:

Supongamos un nodo con tres ramas:

• i_t entrando
• i₁ e i₂ saliendo

Aplicando KCL:

• i_t =i₁ +i₂

Segunda Ley de Kirchhoff (Ley de Tensiones de Kirchhoff)

La Segunda Ley de Kirchhoff, también conocida como la Ley de Tensiones de Kirchhoff (KVL, por sus siglas en inglés), también se basa en el principio de conservación de la energía y establece que:

La suma algebraica de todas las diferencias de potencial (tensiones) alrededor de cualquier lazo cerrado en un circuito es igual a cero.

Matemáticamente:

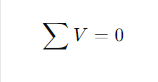
¿Para qué sirve?

• Analizar lazos en circuitos complejos: Permite determinar las tensiones desconocidas en un circuito.
• Diseño de circuitos: Ayuda a asegurar que la energía se conserva y las tensiones se distribuyen adecuadamente.

¿Cómo se usa?

• Identificar lazos cerrados: Encuentra los caminos cerrados en el circuito.
• Asignar tensiones: Define la dirección (sentido horario o antihorario) para recorrer el lazo.
• Aplicar KVL: Escribe una ecuación sumando las tensiones en el sentido recorrido. Las caídas de tensión (en resistencias, por ejemplo) son negativas y las subidas de tensión (fuentes de voltaje) son positivas.
• Resolver el sistema de ecuaciones: Utiliza las ecuaciones obtenidas para resolver las tensiones desconocidas.

Ejemplo

Veamos el sigueinte circuito serie (si tienen dudas sobre este circuito pueden ir a mi perfil donde explico al detalle estos circuitos) con una fuente de voltaje V y dos resistencias 𝑅₁ y 𝑅₂

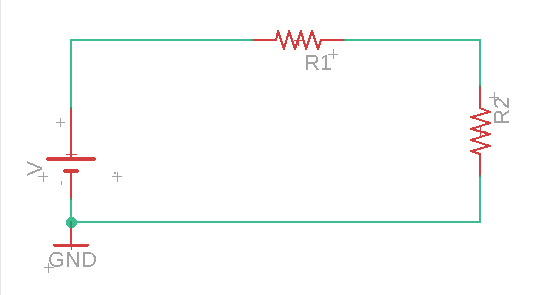
• Fuente de voltaje 𝑉
• Caída de tensión 𝑉_R1 es de R₁
• Caída de tensión 𝑉_R2 es de R₂

Aplicando KVL:
​

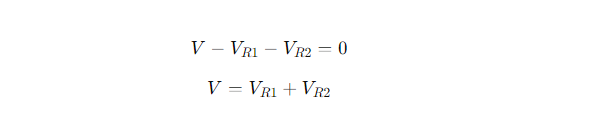
Ventajas de las Leyes de Kirchhoff

• Versatilidad: Pueden aplicarse a cualquier tipo de circuito (resistivo, capacitivo, inductivo).
• Simplicidad: Simplifican el análisis de circuitos complejos descomponiéndolos en nodos y ramas.
• Precisión: Garantizan que se cumplan los principios fundamentales de conservación de la carga y la energía.
• Facilitan el diseño y diagnóstico: Permiten diseñar circuitos con parámetros específicos y diagnosticar problemas al verificar la distribución de corrientes y tensiones.

Aplicación Práctica

Vamos a resolver un ejemplo práctico usando ambas leyes.

Ejemplo Completo

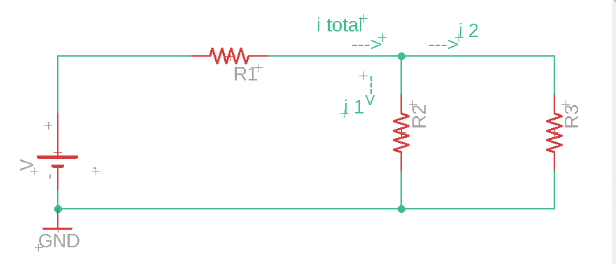
Continuando con el circuito que hemos estado utilizando como ejemplo, ahora le asignaremos valores específicos a los componentes para ilustrar cómo se aplican las fórmulas. Consideremos una fuente de voltaje 𝑉 = 10𝑉, resistencias R₁ = 2 Ω, R₂ = 3 Ω, y R₃ = 5 Ω.

Circuito:

Paso 1: KCL en el Nodo superior

Este Nodo conecta 𝑅₁, 𝑅₂ , y 𝑅₃ sigueindo con lo que estamos estudiando podemos decir por KCL que i_total =i₁ + i₂

Paso 2: KVL en la rama 1 (Fuente 𝑉, 𝑅₁ , 𝑅₂ )

10 V − i₁ ⋅2 Ω − i₂ ⋅3 Ω = 0

10 V= 2i₁ Ω + 3i₂ Ω
​
Paso 3: KVL en el rama 2 (Fuente 𝑉, 𝑅₁, 𝑅₃ )

10 V − i₁ ⋅ 2 Ω - i₃ ⋅ 5 Ω = 0

10 V = 2i₁ Ω + 5i₃ Ω
​
Paso 4: Sistema de ecuaciones

Tenemos tres ecuaciones:

• i₁ = i₂ + i₃
• 10 V = 2i₁Ω + 3i₂Ω
• 10 V = 2i₁Ω + 5i₃Ω

Resolviendo este sistema de ecuaciones, se pueden encontrar los valores de i₁, i₂, i₃.

Conclusión
Las leyes de Kirchhoff son herramientas poderosas y esenciales para el análisis y diseño de circuitos eléctricos, proporcionando un método sistemático para encontrar corrientes y tensiones en cualquier configuración de circuito.

[ENG]

Kirchhoff's First Law (Kirchhoff's Law of Currents)

Kirchhoff's First Law, also known as Kirchhoff's Current Law (KCL), is based on the principle of conservation of electric charge. This law establishes that:

At any node in an electrical circuit, the algebraic sum of all the currents entering and leaving the node is equal to zero.

Mathematically:

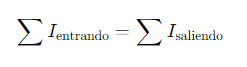(1)

Or simply:

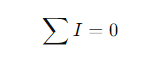
What is it for

This law is useful for analyzing loops in complex circuits such as the combination between series and parallel resistance circuits; It allows you to determine the unknown voltages or currents in a circuit by applying Ohm's law. If you don't remember it, I invite you to visit my blog where I explain it in detail. It also helps ensure that energy is conserved and stresses are properly distributed.

How to use?

First we must be able to identify how many nodes there are in our circuit, and to do this you have to find the points in the circuit where two or more components are connected. Since the definition of a node is:

A Node is a point in the circuit in which three or more currents enter or leave, due to being connected to two or more components.

• Assign currents: Defines a direction for each current entering or leaving the node (can be arbitrary; if chosen incorrectly, the result will be negative, indicating the opposite direction).
• Apply KCL: Write an equation for each node, adding the currents entering and subtracting the currents leaving.
  Solve the system of equations: Use the equations obtained to solve the unknown currents.

Example:

Let's assume a node with three branches:

• i_t entering
• i₁ and i₂ leaving
  Applying KCL:
• i_t =i₁ +i₂

Kirchhoff's Second Law (Kirchhoff's Stress Law)

Kirchhoff's Second Law, also known as Kirchhoff's Voltage Law (KVL), is also based on the principle of conservation of energy and states that:

The algebraic sum of all potential differences (voltages) around any closed loop in a circuit is equal to zero.

Mathematically:

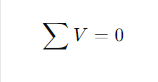
What is it for?

• Analyze loops in complex circuits: Allows you to determine the unknown voltages in a circuit.
• Circuit design: Helps ensure that energy is conserved and voltages are distributed appropriately.

How to use?

• Identify closed loops: Find the closed paths in the circuit.
• Assign voltages: Defines the direction (clockwise or counterclockwise) to traverse the loop.
• Apply KVL: Write an equation adding the voltages in the direction traveled. Voltage drops (in resistors, for example) are negative and voltage rises (voltage sources) are positive.
• Solve the system of equations: Use the equations obtained to solve the unknown tensions.

Example

Let's look at the following series circuit (if you have questions about this circuit you can go to my profile where I explain these circuits in detail) with a voltage source V and two resistors 𝑅₁ and 𝑅₂

• Voltage source 𝑉
• Voltage drop 𝑉_R1 is R₁
• Voltage drop 𝑉_R2 is R₂

Applying KVL:
​

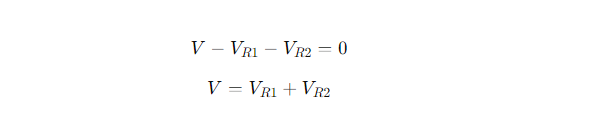
Advantages of Kirchhoff's Laws

• Versatility: They can be applied to any type of circuit (resistive, capacitive, inductive).
• Simplicity: They simplify the analysis of complex circuits by decomposing them into nodes and branches.
• Accuracy: They ensure that the fundamental principles of charge and energy conservation are met.
• They facilitate design and diagnosis: They allow circuits to be designed with specific parameters and diagnose problems by verifying the distribution of currents and voltages.

Practical application

Let's solve a practical example using both laws.

Complete Example

Continuing with the circuit we have been using as an example, we will now assign specific values ​​to the components to illustrate how the formulas apply. Let us consider a voltage source 𝑉 = 10𝑉, resistances R₁ = 2 Ω, R₂ = 3 Ω, and R₃ = 5 Ω.

Circuit:

Step 1: KCL on the Top Node

This Node connects 𝑅₁, 𝑅₂ , and 𝑅₃ continuing with what we are studying we can say by KCL that i_total =i₁ + i₂

Step 2: KVL on branch 1 (Source 𝑉, 𝑅₁ , 𝑅₂ )

10 V − i₁ ⋅2 Ω − i₂ ⋅3 Ω = 0

10 V= 2i₁ Ω + 3i₂ Ω
​
Step 3: KVL on branch 2 (Source 𝑉, 𝑅₁, 𝑅₃ )

10 V − i₁ ⋅ 2 Ω - i₃ ⋅ 5 Ω = 0

10 V = 2i₁ Ω + 5i₃ Ω
​
Step 4: System of equations

We have three equations:

• i₁ = i₂ + i₃
• 10 V = 2i₁Ω + 3i₂Ω
• 10 V = 2i₁Ω + 5i₃Ω

By solving this system of equations, the values ​​of i₁, i₂, i₃ can be found.

Conclusion
Kirchhoff's laws are powerful and essential tools for the analysis and design of electrical circuits, providing a systematic method for finding currents and voltages in any circuit configuration.