[ESP/ENG]Descubriendo el Tao del Circuito Serie RC: Resistencia, Capacitancia y el Tiempo de Carga y Descarga Discovering parte 18|the Tau of the RC Series Circuit: Resistance, Capacitance and the Charging and Discharging Time part 18
[ESP]
¡Hola hermosa comunidad de Hive! 👋
Hoy vamos a explorar un concepto fundamental en la electrónica: el circuito serie con una resistencia (R) y un capacitor (C). Este conocimiento es crucial para comprender y resolver problemas complejos, incluyendo la resolución de circuitos eléctricos en futuras lecciones. 🚀⚡
🌟Introducción al Circuito Serie RC🌟
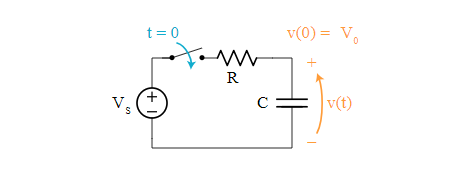
Un circuito serie RC, compuesto por una resistencia y un capacitor conectados en serie, es una de las configuraciones más básicas y esenciales en electrónica. Estos circuitos se utilizan en una variedad de aplicaciones, como filtros, temporizadores y osciladores. El comportamiento de estos circuitos durante los procesos de carga y descarga del capacitor es vital para entender cómo funcionan y cómo se pueden aplicar en la práctica.
🚨Conceptos Básicos del Circuito Serie RC🚨
Cuando se aplica un voltaje a un circuito RC, el capacitor comienza a cargarse a través de la resistencia. La forma en que la carga del capacitor varía con el tiempo se describe mediante una función exponencial. Del mismo modo, cuando el capacitor se descarga a través de la resistencia, la descarga también sigue una curva exponencial.
📝Fórmulas Clave
Carga del Capacitor:
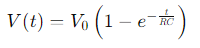
Donde 𝑉(𝑡) es el voltaje a través del capacitor en el tiempo 𝑡, 𝑉0 es el voltaje inicial de la fuente, 𝑅 es la resistencia y 𝐶 es la capacitancia.
Descarga del Capacitor:
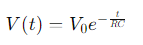
En este caso, 𝑉(𝑡) es el voltaje en el capacitor durante la descarga, 𝑉0 es el voltaje inicial a través del capacitor al comienzo de la descarga, 𝑅 es la resistencia y 𝐶 es la capacitancia.
🛠️Análisis Detallado del Tiempo de Carga y Descarga
Para entender mejor cómo funciona un circuito serie RC, analicemos el proceso de carga y descarga con un ejemplo práctico.
🔍Ejemplo Práctico
Supongamos que tenemos un circuito con una resistencia de 1 kΩ y un capacitor de 100 µF conectado a una fuente de voltaje de 5V. Vamos a calcular el tiempo necesario para que el capacitor se cargue hasta el 63.2% de su voltaje máximo y el tiempo necesario para que se descargue hasta el 36.8% de su voltaje inicial.
Cálculo de Carga
- Constante de Tiempo (τ)
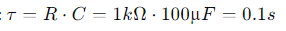
- Voltaje a los 𝑡 = 𝜏:
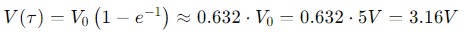
El capacitor se carga al 63.2% de su voltaje máximo en un tiempo igual a la constante de tiempo, que en este caso es 0.1 segundos.
Cálculo de Descarga
- Voltaje a los
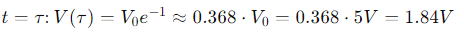
Aplicaciones del Tau en Circuitos Serie RC
El concepto del Tau, en su sentido más amplio, se refiere a la "vía" o "camino" natural de las cosas. En el contexto de los circuitos serie RC, podemos ver el Tao como el flujo natural de la carga y descarga del capacitor, un proceso que sigue las leyes fundamentales de la física y la electrónica. Al igual que en la filosofía Taísta, donde el equilibrio y la armonía son clave, en un circuito serie RC, el equilibrio entre resistencia y capacitancia determina el comportamiento del circuito.
Conclusión
📢 ¡Gracias por Leer! Mantente Conectado para Más Contenido Educativo 📚
Espero que este post te haya sido útil. Si fue así, no olvides dejar un comentario y compartir tus pensamientos o preguntas. 📝
🔔 No te pierdas mis próximas publicaciones donde seguiremos explorando el fascinante mundo de la electrónica y los circuitos. Cada semana, voy a traer nuevos temas, ejemplos prácticos y recursos para que sigas aprendiendo y mejorando tus habilidades.
🤝 Sígueme en mis redes sociales, donde podrás conectarte con otros entusiastas de la electrónica, hacer preguntas y recibir ayuda en tiempo real. ¡Estamos aquí para ayudarte!
📷 Comparte tus Proyectos: Si has aplicado estos conocimientos en tus propios proyectos, ¡nos encantaría verlos! Comparte tus avances y aprende de otros en nuestra comunidad.
🌟 Mantente en Contacto: Sígueme en mis redes sociales para actualizaciones, contenido exclusivo y más consejos sobre electrónica y circuitos. Tu participación y apoyo son lo que hace que esta comunidad crezca y se enriquezca.
¡Nos estamos leyendo! Hasta entonces, sigue explorando, aprendiendo y compartiendo. ¡Juntos, hacemos la electrónica más accesible y emocionante para todos! 🚀✨
[ENG]
Hello beautiful Hive community! 👋
Today we are going to explore a fundamental concept in electronics: the series circuit with a resistor (R) and a capacitor (C). This knowledge is crucial for understanding and solving complex problems, including solving electrical circuits in future lessons. 🚀⚡
🌟Introduction to the RC Series Circuit🌟
An RC series circuit, composed of a resistor and a capacitor connected in series, is one of the most basic and essential configurations in electronics. These circuits are used in a variety of applications, such as filters, timers, and oscillators. The behavior of these circuits during the capacitor charging and discharging processes is vital to understanding how they work and how they can be applied in practice.
🚨Basic Concepts of the RC Series Circuit🚨
When a voltage is applied to an RC circuit, the capacitor begins to charge through the resistor. The way the charge of the capacitor varies with time is described by an exponential function. Similarly, when the capacitor discharges through the resistor, the discharge also follows an exponential curve.
📝Key Formulas
Capacitor Load:
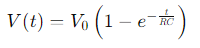
Where 𝑉(𝑡) is the voltage across the capacitor at time 𝑡, 𝑉0 is the initial source voltage, 𝑅 is the resistance and 𝐶 is the capacitance.
Capacitor Discharge:
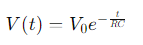
In this case, 𝑉(𝑡) is the voltage across the capacitor during discharge, 𝑉0 is the initial voltage across the capacitor at the beginning of discharge, 𝑅 is the resistance and 𝐶 is the capacitance.
🛠️Detailed Analysis of Loading and Downloading Time
To better understand how an RC series circuit works, let's discuss the charging and discharging process with a practical example.
🔍Practical Example
Suppose we have a circuit with a 1 kΩ resistor and a 100 µF capacitor connected to a 5V voltage source. We are going to calculate the time necessary for the capacitor to charge to 63.2% of its maximum voltage and the time necessary for it to discharge to 36.8% of its initial voltage.
Load Calculation
- Time Constant (τ)
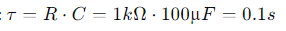
- Voltage at 𝑡 = 𝜏:
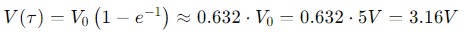
The capacitor charges to 63.2% of its maximum voltage in a time equal to the time constant, which in this case is 0.1 seconds.
Discharge Calculation
- Voltage at
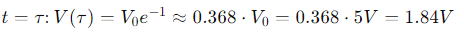
Tao Applications in RC Series Circuits
The concept of Tao, in its broadest sense, refers to the natural "way" or "path" of things. In the context of RC series circuits, we can view Tao as the natural flow of capacitor charging and discharging, a process that follows the fundamental laws of physics and electronics. As in Taoist philosophy, where balance and harmony are key, in an RC series circuit, the balance between resistance and capacitance determines the behavior of the circuit.
Conclusion
📢 Thanks for reading! Stay Connected for More Educational Content 📚
I hope this post has been useful to you. If so, don't forget to leave a comment and share your thoughts or questions. 📝
🔔 Don't miss my next posts where we will continue exploring the fascinating world of electronics and circuits. Each week, I'll bring new topics, practical examples, and resources to keep you learning and improving your skills.
🤝 Follow me on my social networks, where you can connect with other electronics enthusiasts, ask questions and receive help in real time. We are here to help you!
📷 Share your Projects: If you have applied this knowledge in your own projects, we would love to see them! Share your progress and learn from others in our community.
🌟 Stay in Touch: Follow me on my social networks for updates, exclusive content and more tips on electronics and circuits. Your participation and support are what make this community grow and enrich.
We are reading each other! Until then, keep exploring, learning and sharing. Together, we make electronics more accessible and exciting for everyone! 🚀✨
Interesante sorpresa @profwhitetower.
Pase a conocer a un lector y me encuentro con un técnico que además es filósofo.
Cuando vi la palabra Tao, pensé que se trataba de alguna clase de siglas, pero sorpresa se trata del impalpable y siempre presente Tao.
Ha sido un placer.
¡Hola! 😊
¡Muchas gracias por tu comentario! Me alegra mucho que hayas disfrutado de la publicación. Es genial poder combinar la técnica con un poco de filosofía, y el Tao, en este caso, nos da una perspectiva interesante sobre el tiempo de carga y descarga en los circuitos. Es un placer compartir estos conocimientos con ustedes.
¡Espero seguir trayéndoles más sorpresas y contenidos interesantes! 🙌📚🔧
Saludos cordiales,
@profwhitetower
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @profwhitetower! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 100 replies.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: