physicalquantity 0.1.0 (python): Walkthrough usage and the added support for planck units and log-scale units.
Before I get to the planck units and log scale features just added to the physicalquantity library, I'm going to give a litle bit of an introduction to physical quantities and units in general.
Physical quantities
We all know we shouldn't compare apples and oranges, you can't do math with apples and oranges unless you do fruits math, losing some of the core attributes of both the apples and the oranges.
In physics things are a bit different. The laws of physics as they have been discovered through the ages have shown us that maybe you can't compare core physics concepts, they are mathematically related. Its like in physics you cant subtract apples from oranges, but you can multiply and divide them.
For example, you can multiply an electric potential measured in volts and multiply it by an electric current measured in amperes. The result will be a power measured in watts that you can divide my an acceleration measured in meters per second, and the result will be a force measured in newton.
Physics is made up of circumstancial relationships between measurable physical quantities that are quentified in terms of physical units. There are about three dozen physical phenonema where we as humans have created physical units for. The laws of physics allow us to express any of these units in terms of a collection of others.
Multiple units for the same thing
Many of the things we have been using throughout history have been quantified long before most of humanity was really concerned about how things would fit together in a mathmatical framework for physics. Different groups of people picked different units for the same thing. In some cases even, science itself picked different units because they are more usable in debates when talking about different scales.
You can do all math with these different units that you need to do, not just multiplications and divisions, you can add a trillion miles to a lightyear and express the result in planck units of time. The result will be a massively big number, but you can do it. For distance its just a simple measure of scaling.
There are also units that need a little more than scaling. For example the temperature measured in degrees celcius has the exact same scale as temperature measured in degrees Kelvin, but it exists at an offset of 273.15 degrees Kelvin.
The Fahrenheid unit for temperature requires both scaling and an offset in order to be usable in equations with other temperatures. The fahrenheid scale exists at an offset of 255.3722 degree Kelvin with a scaling factor of about 0,5556.
I think this is probably the simplest usecase for the Physical Quantity library to show, so lets look at some code.
from physicalquantity import PhysicalQuantity as q
t1 = q(17,"celsius")
t2 = q(62.5,"fahrenheit")
t3 = t1 - t2
print(t3)
The result of this code:
0.055577774999983176 kelvin
The result gets automaticly normalized to degrees kelvin. It is possible we don't want this and want the result in fahrenheid instead.
print(t3.as_absolute("fahrenheit"))
-459.5699199682344 fahrenheit
We just saw the automated normalization to Kelvin once we started doing some operations. Kelvin is one of the SI units that we will discuss in the next section. The SI system of units is one collection of unit standarizations that we can noramlize to with teh Physical Quantity library. The other one, a new one, and unfortunately an incomplete one is the Planck system of units.
We will look at planck units later in this blog post, but this is the right place to demonstrate the basics of normalization.
t1 = q(1000000,"fahrenheit")
print(t1)
print(t1.normalized())
print(t1.normalized(planck_units=True))
The result:
1000000.0 fahrenheit
555810.9278000001 kelvin
3.923095193750453e-27 plancktemperature
We took the insane temperature of one million degrees fahrenheit and normalized is in two different ways. The standard SI units way resulting in a temperature of 555811 degrees kelvin, and the Planck units way, resulting in a miniscule number of 3.9e-27 planck units of temperature That is 0.0000000000000000000000000039 plancktemperature.
SI units
We spoke before about SI units. As stated, it is possible to define units of one physical thing in an expression using only units of other physical things. We sometimes already do this. Velocity and acceleration don's have their own units, at least not in standard terms. There is knot for velocity, c the speed of light can be used to express velocity (we will revisit this when we get to planck units) and sometimes g is informally used as unit of acceleration, but normally both standerized and non standarized usage use some kind of distance unit per time unit. Meters per second; miles per hour; etc.
Mathematically there are multiple groups of seven ot more units that could be used as somehow fundamental units that all other units are expressed in. This doesn't mean that they are physically fundamental, but if you pick seven units, you can buikd a system around those that can express all the others. The system of SI units has done exacly that. It is important to remember this. For example, it is generaly considered that speed is more fundamental than distance. SI has chosen distance though as one of the core units.
So what are the core seven units that SI units all revolve around?
- metre : unit of length
- kg : unit of mass
- second : unit of time
- ampere : unit of electical current
- kelvin : unit of temperature
- mole : unit of substance
- candela : unit of intensity
Lets look at a few examples of other units and see how this works:
- hertz : Unit of frequency, can be expressed in terms of one divided by the unit of time.
- coulomb : unit of charge, can be expressed in terms of the unit of current times the unit of time.
- newton: unit of force, can be expressed in unit of mass times unit of distance divided by the square of the unit of time.
What we see that if we have a physical quantity of something, the unit to use to describe that something can be expressed as a list of seven integer values, one integer for each of the seven core units.
Lets do just that for the above four units and a few more
| metre | kg | second | ampere | kelvin | mole | candela | |
|---|---|---|---|---|---|---|---|
| hertz | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| newton | 1 | 1 | -2 | 0 | 0 | 0 | 0 |
| coulomb | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Now comes the fun thing, if we represent a physical quantity as a floating point number and this array of integers representing their units, we can do some apples and oranges math so to speak. We still can't subtract apples from oranges, we can however multiply and divide without loss of information.
Units based operations in Physical Quantity lib
Multiplying two random physical quantities means multiplying the value and adding up the unit integers. Dividing means dividing the values and subtracting with the unit integers. Let's demonstrate.
i = q(4.2,"ampere")
v = q(17.5,"volt")
p = i*v
s = q(80,"kilometer")/q(1,"hour")
f = p/s
for ent in [i,v,p,s,f]:
un = ent.normalized()
print(un)
print(un.__repr__())
The result:
4.2 ampere
physicalquantity.PhysicalQuantity(4.2,ampere,[0, 0, 0, 1, 0, 0, 0],1.0,0.0)
17.5 volt
physicalquantity.PhysicalQuantity(17.5,volt,[2, 1, -3, -1, 0, 0, 0],1.0,0.0)
73.5 watt
physicalquantity.PhysicalQuantity(73.5,watt,[2, 1, -3, 0, 0, 0, 0],1.0,0.0)
22.22222222222222 m/s
physicalquantity.PhysicalQuantity(22.22222222222222,None,[1, 0, -1, 0, 0, 0, 0],1.0,0.0)
3.3075 newton
physicalquantity.PhysicalQuantity(3.3075,newton,[1, 1, -2, 0, 0, 0, 0],1.0,0.0)
In the above example we see everything comming together as expected, but during development its important to still check because according to the rules of the game many things are possible that are not correct. Lets add a bug to the above code.
i = q(4.2,"ampere")
v = q(17.5,"volt")
p = i*v
s = q(80,"kilometer")/q(1,"hour")
f = s/p # bug
for ent in [i,v,p,s,f]:
un = ent.normalized()
print(un)
print(un.__repr__())
Result:
4.2 ampere
physicalquantity.PhysicalQuantity(4.2,ampere,[0, 0, 0, 1, 0, 0, 0],1.0,0.0)
17.5 volt
physicalquantity.PhysicalQuantity(17.5,volt,[2, 1, -3, -1, 0, 0, 0],1.0,0.0)
73.5 watt
physicalquantity.PhysicalQuantity(73.5,watt,[2, 1, -3, 0, 0, 0, 0],1.0,0.0)
22.22222222222222 m/s
physicalquantity.PhysicalQuantity(22.22222222222222,None,[1, 0, -1, 0, 0, 0, 0],1.0,0.0)
0.30234315948601664 s/mKg
physicalquantity.PhysicalQuantity(0.30234315948601664,None,[-1, -1, 2, 0, 0, 0, 0],1.0,0.0)
We can see in the output that things are wrong, but its better to actually check these things while developing using asserts.
i = q(4.2,"ampere")
v = q(17.5,"volt")
p = i*v
s = q(80,"kilometer")/q(1,"hour")
f = s/p # bug
assert f.same_dimensions("force")
for ent in [i,v,p,s,f]:
un = ent.normalized()
print(un)
print(un.__repr__())
If you run this code you get an assertion error because you expected a force and got something completely different.
Serialization
My Physical Quantity library isn't the only python library available on pypi. It wasn't the first either. It was writen primaraly because my personal usecase needed these physical units to be serializable and used across microservices. So while the functionality above so far is not that unique, combined with the ability to represent it in a serializable structure, it has a unique value that is hard to replicate with any of the alternative libs. So lets show it in action.
There are two options for serialization. Either use the json method and the from_json function to serialize a single quantity to json, or use the as_dict method and from_dict function when you want to serialize a composite or want to use other serialization forms such as yaml or pickle.
import yaml
f = q(9.8,"newton")
s = q(13,"kilometer")/q(19,"hour")
composit = { "force": f.as_dict(), "speed": s.as_dict() }
print(f.json())
print()
print(s.json())
print()
print(yaml.dump(composit))
{
"unit": "newton",
"value": 9.8
}
{
"unit": {
"dimensions": {
"length": 1,
"time": -1
}
},
"value": 0.19005847953216373
}
force:
unit: newton
value: 9.8
speed:
unit:
dimensions:
length: 1
time: -1
value: 0.19005847953216373
Logaritmic scale units
Untill now, the Physical Quantity only supported linear scale physical units.
There are a couple of units though that use a logaritmis scale.
The new 0.1 version of the lib support one way use of these values. That is, you now create linear scale entities from a log scale notation. Not (yet) the other way around.
Units currently supported are:
- dB : Log 10 scale based unit for sound, translates to pascal
- dBm : Log 10 scale based unit for signal strength, translates to watt
- pitch : Log 2 scale based unit for frequency, translates to hertz
- dbW : Like dBm but at watt base rather than miliwatt
- dbV : Like dbW but for electrical potential instead of power, translates to volt
- dbA : Like dbW but for electrical current instead of power, translates to ampere
For pitch we have another fun little adition. The from_note function allows you to create a pitch physical quantity from a musical note.
from physicalquantity import from_note
print(q(39,"dB"))
print(q(44,"dBm"))
print(from_note("F6"))
0.1588656469448563 pascal
25.118864315095802 watt
1396.9129257320155 hertz
Planck units.
As we saw at the start of this blog post, next to SI units, there exist another set of units that we can use to normalize to, or that might be our inputs. While internaly our library works with SI units, the 0.1.0 version now has support for entering and normalizing to planck units.
So what are planck units? Well, we can look at planck units in two different ways. We can look at it from the perspective that some of the planck units represent physical limits beyond what the math of physics that we currently have runs into problems, and YouTube is full with videos talking about planck units from that perspective. We can also look at planck units as a convention for physical units that makes many of our laws of physics simpler and much easier to work with. I think this is the truly interesting way to look at it.
We all know about Einstein's equation E=mc². The c in this equation is the speed of light, 299792568 meters per seconds squared. The speed of light is one of a small set of fundamental constants of physics.
But these constants are only fundamental because of the units we chose for doing physics with. Humans came up with the meter and with the second as measures of distance and time. The m is mass in kg, another unit we came up with, energy in joule that maps to length mass and time.
If any of the three units, time, mass, or distance was chosen differently, c would get another value. So what if we use this info to try and simplify physics? Let's just equate c to one!
To do that, we need to say that the speed of light equates one unit of length per unit of time. We need to choose the units of lenght and time in such a way that this holds true.
The speed of ligth, or c isn't the only fundamental constant of physics, and if it was, it wouldn't be enough to choose units for length, mass and time, there will be too many possibilities to choose from.
In the end we have:
- c : The speed of light
- G : The gravitational constant
- k : The Boltzmann constant
- h or ℏ: The planck constant
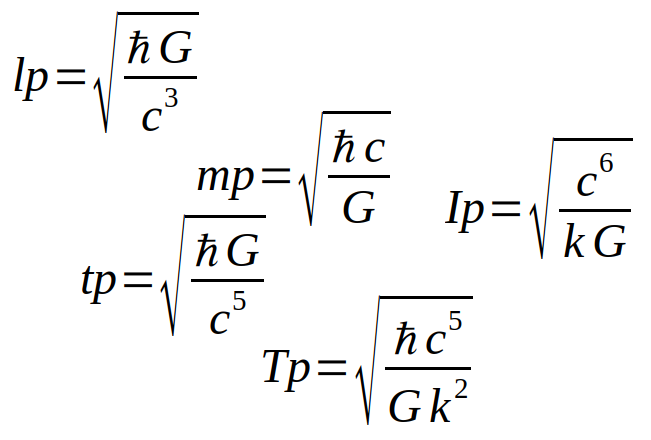
If we define all of these four fundamental constants of nature as having the value of one, physics becomes a whole lot simpler as all of these constants just disapear from the equations. Doing this gives us enough hooks to find one and only one unit for most of our physical quantities. Not all though.
| SI unit | Planck unit | Scale | |
|---|---|---|---|
| length | meter | plancklength | 1.62e-35 meter |
| mass | kg | planckmass | 2.18e-8 kg |
| time | second | plancktime | 5.39e-44 second |
| current | ampere | planckcurrent | 3.48e25 ampere |
| temperature | kelvin | plancktemperature | 1.42e32 Kelvin |
| substance | mole | - | - |
| intensity | candela | - | - |
We see that planck length and time are insanely small while planck current and temperature are insanely high. Planck mass is small but still within the sizes that have intuitive meaning to us as humans. It should be understandable that, however much geeks like me would like it because it really simplifies physics a lot, that you don't want to go to the market to buy a 5.0e104 planck volumes bottle of soda, or set your oven to 3.5e-30 planck temperatures. These units are not very usefull for every day usage because of their sizes. But you can use them from the library now.
print(q(220,"celsius").normalized(planck_units=True).json())
{
"unit": "plancktemperature",
"value": 3.480813884778815e-30
}
print(q(60,"megaplanckmass").normalized().json())
{
"unit": "kg",
"value": 1.305842787845235
}
To do
It was a long time since I did anything about this library, and it has been fun to add the new features. There are still some pending issues to look at. For one the fact that the whole log scale thing currently only works in one direction. The project currently doesn't have my priority, but when I'm going to work on it again, I'll be sure to add a method for converting linear scale units back to logaritmin ones such as pitch, dB and dBm.
The library is currently quite forgiving about undefined or ambiguously defined planck units. There are currently no accepted planck units for substance and intensity. Even the planck unit for electrical current seems to still have a few alternatives. I tried to use the one that seems to be the most widely accepted, but I'm no physisist, so its possible that its not actualy the right one. A future version is likely to give the user some finer levels of control to choose a different interpretation for these. Sumarizing, I hope to one day at the following features:
- A method for two way conversions for log-scale units
- A way to choose different behaviour for ill defined plank units
- Option to switch between loose normalization with planck units and runtime errors
- Option to choose for one of the alternative interpretations of planck current.
- Option to choose between using the SI unit for substance, or alternatively a more fundamental scaled down version (mole divided by 6.02214076e23)
It seems that substance and intensity will remain a problem that I won't be able to solve, but I will try to add options for fine control for the user as to these are handled, as I hope to do for electrical current.
Closing
I hope that this lib and its new aditions are going to be usefull to people other than myself. As stated, its not a high priority project. I build it in my spare time because I needed to serialize and work with physical quantities accross a microservice architecture while noone at my day job saw the importance of being units safe across microservices. I'm currently not aware of anyone else using this lib right now, but I think it is a lib that can be of use to others.
So if you read this and I've convinced you of its use, give it a try and give me some feedback if you can.
I'm also really interested in feedback from people with a physics background about how to best fill in the gaps between the SI units and the Planck units that I talked about in this blog.
Haha really not a fan of math or physis i find it too complicated enough, i just let it go even in while in school focus more on biology has its more practical