Endlicher Automat in c++, Wortprüfung einer regulären Grammatik gemäß des Typ-3 der Chomsky Hierarchie

Nun ist es soweit. Der endliche Automat wurde um die Funktionen isValidWord und examineWord erweitert, um ein eingegebenes Wort auf seine Gültigkeit gemäß dieses endlichen Automaten zu prüfen.

Diese vier Wörter werden auf Gültigkeit überprüft: ABCDBEEA, ABCCDBC, DEAABE und CAABCDEED.
Nach der Ausführung dieser Anwendung steht fest, dass die Wörter 1 und 3 gültig, aber die Wörter 2 und 4 ungültig sind.
Das 2. Wort ist ungültig, da es keinen Zustandsübergang von C nach C gibt.
Das 4. Wort ist ungültig, da es keinen Zustandsübergang von E nach D gibt.

Und so kann man endliche Automaten nutzen um Wörter eines Eingabealphabet zu prüfen. Oder genauer, um zu prüfen ob ein Wort einer regulären Grammatik des Typ-3 gemäß der Chomsky Hierarchie entspricht.
Das nächste mal geht es um die Implementierung einer nichtdeterministischen Turingmaschine mit Gödelisierung... Garantiert nicht!😂😂😂

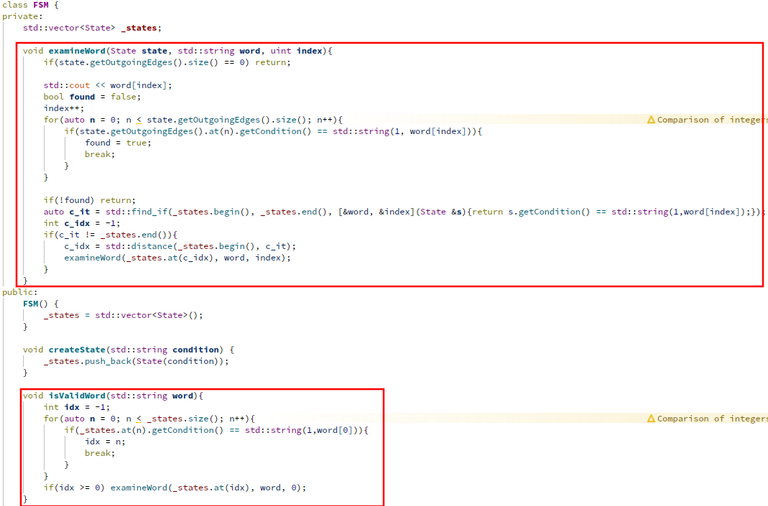
Die Veränderungen im Code im Vergleich zum letzten Beitrag habe ich rot markiert.

void examineWord(State state, std::string word, uint index){
        if(state.getOutgoingEdges().size() == 0) return;

        std::cout << word[index];
        bool found = false;
        index++;
        for(auto n = 0; n < state.getOutgoingEdges().size(); n++){
            if(state.getOutgoingEdges().at(n).getCondition() == std::string(1, word[index])){
                found = true;
                break;
            }
        }

        if(!found) return;
        auto c_it = std::find_if(_states.begin(), _states.end(), [&word, &index](State &s){return s.getCondition() == std::string(1,word[index]);});
        int c_idx = -1;
        if(c_it != _states.end()){
            c_idx = std::distance(_states.begin(), c_it);
            examineWord(_states.at(c_idx), word, index);
        }
    }

void isValidWord(std::string word){
        int idx = -1;
        for(auto n = 0; n < _states.size(); n++){
            if(_states.at(n).getCondition() == std::string(1,word[0])){
                idx = n;
                break;
            }
        }
        if(idx >= 0) examineWord(_states.at(idx), word, 0);
    }