儿子最近考试总考砸，而学校每天几乎都有考试，所以放学时接到孩子，往往就看到他一副失落的样子，对我说：“完蛋了，XX（科目）又考砸了。”

我就安慰他说：“没事呀，考砸了是好事，知道自己哪里薄弱，咱努力去弥补就好了。成绩不重要，重要的是学到知识。”

儿子听到后，总算安心了不少，然后又开始喋喋不休地给我讲学校了发生的趣事。哎，这孩子啥时候能长大呀，整天就关心这些乱七八糟的事，心思没在学习上，那成绩能上来嘛？

不过想想做个无忧无虑的少年也挺好的，他若真的“两耳不闻窗外事，一心只读圣贤书”，恐怕我又会觉得恐怖了。

(图源 ：pixabay)

话说每次他考砸之后，我和媳妇都会帮他看看试卷，看看到底是哪里出的问题。

一元一次方程

昨天数学考试，错题中的一道很有趣，给出几个方程式，让选出那几个是一元一次方程。

话说我们一看，这多简单的送分题呀，一元一次方程的定义如下：

一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式。

那么就按定义判断呗，比如喊两未知数的，未知数次数超过1的，两边存在分式的，那就都刨除掉呗，剩下的就是一元一次方程呗。

于是我顺利的给出了答案，结果和儿子选的一样，不出意料，都错了。😡

于是我又仔细看了一下题目中给的几个式子，其中有这样两个贼眉鼠眼的，
一个是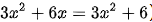：，另一个是类似2/x=1。

我仔细一样，第一个式子中的两个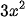，是可以抵消掉的；第二个式子中的x虽然在分母为止，但是可以把两端都乘以x，从而把分母为止的x消除掉。

那这么说，这两个式子也是一元一次方程喽，可是一看答案，第一个式子算一元一次方程，第二个却不算！😡

我就怒了，明明不化简，都不符合定义，化简后都符合定义，所以要么都算，要么都不算，整的一个算，一个不算，这是什么鬼东西！

于是又查了百度百科等资料，其中明确指出：

可以通过等式性质化简而成为一元一次方程的整式方程（如）也属于一元一次方程。

而2/x=1或者2/x +x = 2/x +10，这样的，尽管能够化简，化简后也确实是一元一次方程，但因为原始式子含分式，所以就不算一元一次方程。

哎，这玩意，人家咋定义的咋说的就有理吧，如果当年我负责定义这事，并且规定化简后符合一元一次方程定义的都算是一元一次方程，或者判断是否是一元一次方程只看原式是否符合，而不进行化简，那么无论无何，我都不会错上两次呀。

而且我觉得考察这个有意义嘛？我会化简会解方程才是更有意义的事情吧？哎😔，无语。

单项式

又想到前些天儿子考试错的另外一道题，和一元一次方程有异曲同工之坑。

题目同样是给出一堆式子，让选出其中的单项式，儿子选错了，我上来也同样选错了。

单项式定义如下：

由数和字母的积组成的代数式(此处应为整式）叫做单项式，单独的一个数或一个字母也叫做单项式(例：0可看做0乘a，1可以看做1乘指数为0的字母，b可以看做b乘1)，分数和字母的积的形式也是单项式。

所以1/x算不算单项式呢？我认为既然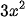算是单项式，那么1/x也应该算呀？因为这个等价于x的（-1）次幂。

但是同样，我又错了，无论它是否等价x的（-1）次幂，只要分母位置有字母（常数不算，比如Π），那么就算分式，就不符合单项式的定义啦（因为单项式属于整式）。

哎，一个头三个大，考这个不如问我茴香豆的茴有几种写法！😡

方向角

说到错误，前些天儿子和我又栽入同一个坑中，一个带方向的坐标和一堆角，然后问其中射线ON的方向是多少。

经过计算，ON和与X轴成25度角，且在X轴上方，那么我瞬间得出结论，东偏北25°。结果发现答案选项中除了东偏北25°，还有北偏东75°。

那还用说嘛？当然选择度数小的啦，放着偏25度的小角度不说，说个大角度，怎么就感觉怪怪的呢？

结果一看正确答案，就是北偏东75°！😡

我又怒了，于是怒查百度，关于方向角定义如下：

方向角指的是采用某坐标轴方向作为标准方向所确定的方位角。有时，方向角是从正北或正南方向到目标方向所形成的小于九十度的角。

下边还有详细的解释：

方向角乃一平面角，系一直线与南北方向线（参见方位角条）间所夹之角，仍系用来标出两点方位之一法。与方位角不同者，方向角系分由南北起算，角度值在零度及九十度之间。方向角之表出方式乃是在角度值之前冠以南北字样，其后则书出东西字样。

好吧，我又失败了，又是该死的约定。

(图源 ：pixabay)

只是我感觉我上学的时候，都没学过也没考过这些内容呀？现在咋都教这些（考这些）内容呢？况且关于方向角，教科书我翻了一遍，根本没有相关内容呀！

真害怕哪天，试卷上出现一道填空题：请写出茴香豆的十种写法！我感觉按当前的趋势，会有这么一天的。

相关链接

• 一元一次方程
• 单项式
• 方向角